* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 8
Coriolis force wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Old quantum theory wikipedia , lookup
Tensor operator wikipedia , lookup
Center of mass wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Transmission (mechanics) wikipedia , lookup
Fictitious force wikipedia , lookup
Equations of motion wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Jerk (physics) wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Virtual work wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Mitsubishi AWC wikipedia , lookup
Photon polarization wikipedia , lookup
Mass versus weight wikipedia , lookup
Accretion disk wikipedia , lookup
Classical central-force problem wikipedia , lookup
Centripetal force wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Angular momentum operator wikipedia , lookup
Moment of inertia wikipedia , lookup
Angular momentum wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Torque wrench wikipedia , lookup
Friction-plate electromagnetic couplings wikipedia , lookup
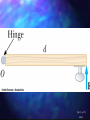
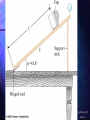
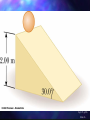
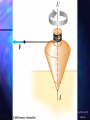
Chapter 8 Rotational Equilibrium and Rotational Dynamics Fig 8.1, p.221 Slide 1 Torque Torque, , is the tendency of a force to rotate an object about some axis Fd is the torque – symbol is the Greek tau F is the force d is the lever arm (or moment arm) Lever Arm The lever arm, d, is the perpendicular distance from the axis of rotation to a line drawn from the axis of rotation to a line drawn along the the direction of the force d = L sin Φ FL sin An Alternative Look at Torque The force could also be resolved into its x- and ycomponents The x-component, F cos Φ, produces 0 torque The y-component, F sin Φ, produces a non-zero torque FL sin Torque and Equilibrium First Condition of Equilibrium F 0 Fx 0 and Fy 0 This is a statement of translational equilibrium To ensure mechanical equilibrium, you need to ensure rotational equilibrium as well as translational The Second Condition of Equilibrium states The net external torque must be zero 0 Mechanical Equilibrium In this case, the First Condition of Equilibrium is satisfied F 0 500N 500N The Second Condition is not satisfied Both forces would produce clockwise rotations 500Nm 0 •If the object is in equilibrium, it does not matter where you put the axis of rotation for calculating the net torque. •When solving a problem, you must specify an axis of rotation and maintain that choice consistently throughout the Fig 8.12a, p.228 Slide 17 Fig 8.12bc, p.228 Slide 18 Torque and Angular Acceleration An object that rotates at uniform angular velocity has zero net torque acting on it When a rigid object is subject to a net torque, it has an angular acceleration The angular acceleration is directly proportional to the net torque The relationship is analogous to Newton’s Second Law ∑F = ma Moment of Inertia The rotational analog of mass is called the moment of inertia, I, of the object 2 2) (SI units are kg m I mr angular acceleration is directly proportional to the net torque angular acceleration is inversely proportional to the moment of inertia of the object I **The moment of inertia depends upon the location of the axis of rotation Moment of Inertia of a Uniform Ring Image the hoop is divided into a number of small segments, m1 … These segments are equidistant from the axis I miri MR 2 2 Other Moments of Inertia Angular Momentum Like relationship between force and momentum in a linear system, we can a relationship between torque and angular momentum Angular momentum is defined as L=Iω and L t If the net torque is zero, the angular momentum remains constant Fig 8.29, p.240 Slide 38 Fig P8.55, p.252 Slide 70 Coordinates of the Center of Gravity The coordinates of the center of gravity can be found from the sum of the torques acting on the individual particles being set equal to the torque produced by the weight of the object mi x i mi y i x cg and y cg mi mi Example – uniform ruler Experimentally Determining the Center of Gravity The wrench is hung freely from two different pivots The intersection of the lines indicates the center of gravity A rigid object can be balanced by a single force equal in magnitude to its weight as long as the force is acting upward through the object’s center of gravity Fig UN8.1, p.224 Slide 8 =41.8° Fig P8.64, p.253 Slide 75 Example of a Free Body Diagram Isolate the object to be analyzed Draw the free body diagram for that object Include all the external forces acting on the object Rotational Kinetic Energy An object rotating about some axis with an angular speed, ω, has rotational kinetic energy ½Iω2 Energy concepts can be useful for simplifying the analysis of rotational motion Total Energy of a System Conservation of Mechanical Energy (KEt KEr PEg )i (KEt KEr PEg )f Remember, this is for conservative forces, no dissipative forces such as friction can be present Fig 8.25, p.236 Slide 36 Fig P8.43, p.250 Slide 66 Fig 8.14, p.229 Slide 25