Download Tuesday, June 26, 2007 - UTA High Energy Physics page.

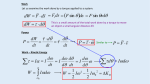
PHYS 1443 – Section 001
Lecture #15
Tuesday, June 26, 2007
Dr. Jaehoon Yu
•
•
•
•
Rotational Kinetic Energy
Work, Power and Energy in Rotation
Angular Momentum & Its Conservation
Similarity of Linear and Angular Quantities
Today’s homework is HW #7, due 7pm, Friday, June 29!!
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
1
Moment of Inertia
Rotational Inertia:
For a group
of particles
Measure of resistance of an object to
changes in its rotational motion.
Equivalent to mass in linear motion.
I   mi ri
2
i
What are the dimension and
unit of Moment of Inertia?
For a rigid
body
I   r 2 dm
ML 
2
kg  m
2
Determining Moment of Inertia is extremely important for
computing equilibrium of a rigid body, such as a building.
Dependent on the axis of rotation!!!
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
2
Rotational Kinetic Energy
y
vi
mi
ri
q
O
x
What do you think the kinetic energy of a rigid object
that is undergoing a circular motion is?
1
1
2
2 

m
v
Kinetic energy of a masslet, mi,
Ki

m
r
i i
i i 
2
2
moving at a tangential speed, vi, is
Since a rigid body is a collection of masslets, the total kinetic energy of the
rigid object is
1
1
2 
2 
K R   Ki   mi ri     mi ri 
2 i
2 i

i
Since moment of Inertia, I, is defined as
I   mi ri
2
i
The above expression is simplified as
Tuesday, June 26, 2007
1 
K R  I
2
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
3
Total Kinetic Energy of a Rolling Body
What do you think the total kinetic
energy of the rolling cylinder is?
P’
CM
Since it is a rotational motion about the point
P, we can write the total kinetic energy
1
K  I P 2
2
2vCM
vCM
Where, IP, is the moment of
inertia about the point P.
Using the parallel axis theorem, we can rewrite

P

1
1
1
1
2
2
2
2
2 2
K  I P  I CM  MR   I CM   MR 
2
2
2
2
1
1
Since vCM=R, the above
2
2
K  I CM   MvCM
relationship can be rewritten as
2
2
What does this equation mean?
Rotational kinetic
energy about the CM
Translational Kinetic
energy of the CM
Total kinetic energy of a rolling motion is the sum
of the rotational kinetic energy about the CM
Tuesday, June 26, 2007
And the translational
PHYS 1443-001, Summer 2006
kinetic of the CM
Dr. Jaehoon Yu
4
Kinetic Energy of a Rolling Sphere
R

h
q
vCM
Since vCM=R
What is the speed of the
CM in terms of known
quantities and how do you
find this out?
Let’s consider a sphere with radius R
rolling down a hill without slipping.
1
1
2
2 2
K  I CM   MR 
2
2
2
1
 vCM   1 Mv 2
 I CM 
CM

2
2
 R 
1  I CM
 2
  2  M vCM
2 R

Since the kinetic energy at the bottom of the hill must
be equal to the potential energy at the top of the hill
1  I CM
 2


M
 2
vCM  Mgh
K
2 R

vCM 
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
2 gh
1  I CM / MR 2
5
Example for Rolling Kinetic Energy
For solid sphere as shown in the figure, calculate the linear speed of the CM at the
bottom of the hill and the magnitude of linear acceleration of the CM. Solve this problem
using Newton’s second law, the dynamic method.
What are the forces involved in this motion?
Gravitational Force, Frictional Force, Normal Force
Newton’s second law applied to the CM gives
n
f
M
h
F
F
q
Mg
x
 Mg sin q  f  MaCM
y
 n  Mg cosq  0
Since the forces Mg and n go through the CM, their moment arm is 0

and do not contribute to torque, while the static friction f causes torque CM
We know that
I CM 
2
MR 2
5
aCM  R
We
obtain
2
MR 2
I CM 
2
f 
 aCM   MaCM
5
R  R  R  5


Substituting f in
dynamic equations
Tuesday, June 26, 2007
 fR  I CM 
7
Mg sin q  MaCM
5
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
aCM 
5
g sin q
7
6
Work, Power, and Energy in Rotation
f
dq r
ds
O
Let’s consider a motion of a rigid body with a single external
force F exerting on the point P, moving the object by ds.
The work done by the force F as the object rotates through
the infinitesimal distance ds=rdq is
dW  F  ds   F cos( 2  f )  rdq  F sin f rdq
What is Fsinf?
What is the work done by
radial component Fcosf?
Since the magnitude of torque is rFsinf,
The rate of work, or power, becomes
Zero, because it is perpendicular to the
displacement.
dW  rF sin f dq  dq
P
The rotational work done by an external force
equals the change in rotational Kinetic energy.
The work put in by the external force then
Tuesday, June 26, 2007
The tangential component of the force F.
How was the power
dW  dq
  defined in linear motion?


dt
dt
 d   I  d  dq   I  


I




I




dq
d
 dq  Id
qf
 dt 
f
W  q  dq  
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu

 dq  dt 

dW   dq  Id
Id 
1 2 1 2
I f  I i
2
27

Angular Momentum of a Particle
If you grab onto a pole while running, your body will rotate about the pole, gaining
angular momentum. We’ve used linear momentum to solve physical problems
with linear motions, the angular momentum will do the same for rotational motions.
Let’s consider a point-like object ( particle) with mass m located
at the vector location r and moving with linear velocity v
The angular momentum L of this
Lrp
particle relative to the origin O is
What is the unit and dimension of angular momentum?
Note that L depends on origin O. Why?
kg  m2 / s [ ML2T 1 ]
Because r changes
What else do you learn? The direction of L is +z
Since p is mv, the magnitude of L becomes L  mvr sin f
What do you learn from this?
Tuesday, June 26, 2007
If the direction of linear velocity points to the origin of
rotation, the particle does not have any angular momentum.
If the linear velocity is perpendicular to position vector, the
particle
moves exactly the same way as a point on a 8rim.
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
Angular Momentum and Torque
dp
 F  dt
Can you remember how net force exerting on a particle
and the change of its linear momentum are related?
Total external forces exerting on a particle is the same as the change of its linear momentum.
The same analogy works in rotational motion between torque and angular momentum.


  r  F  r  dt
Net torque acting on a particle is
z
dr
dp
dp
dL d  r  p 

 pr
 0r 

L=rxp
dt
dt
dt
dt
dt
O
x
r
y
m
f
Why does this work?
p
Thus the torque-angular
momentum relationship
dp
 
Because v is parallel to
the linear momentum
 
dL
dt
The net torque acting on a particle is the same as the time rate change of its angular momentum
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
9
Angular Momentum of a System of Particles
The total angular momentum of a system of particles about some point
is the vector sum of the angular momenta of the individual particles
L  L1  L2 ......  Ln   L i
Since the individual angular momentum can change, the total
angular momentum of the system can change.
Both internal and external forces can provide torque to individual particles. However,
the internal forces do not generate net torque due to Newton’s third law.
Let’s consider a two particle
system where the two exert
forces on each other.
Since these forces are the action and reaction forces with
directions lie on the line connecting the two particles, the
vector sum of the torque from these two becomes 0.
Thus the time rate change of the angular momentum of a
system of particles is equal to only the net external torque
acting on the system
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu

ext
dL

dt
10
Example for Angular Momentum
A particle of mass m is moving on the xy plane in a circular path of radius r and linear
velocity v about the origin O. Find the magnitude and direction of angular momentum with
respect to O.
Using the definition of angular momentum
y
v
L  r  p  r  mv  mr  v
r
O
x
Since both the vectors, r and v, are on x-y plane and
using right-hand rule, the direction of the angular
momentum vector is +z (coming out of the screen)

The magnitude of the angular momentum is L  mr  v  mrv sin f  mrv sin 90  mrv
So the angular momentum vector can be expressed as
L  mrvk
Find the angular momentum in terms of angular velocity .
Using the relationship between linear and angular speed
2
L  mrvk  mr 2k  mr   I
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
11
Angular Momentum of a Rotating Rigid Body
z
Let’s consider a rigid body rotating about a fixed axis
Each particle of the object rotates in the xy plane about the z-axis
at the same angular speed, 
L=rxp
O
y
m
r
f
x
Magnitude of the angular momentum of a particle of mass mi
about origin O is miviri
2
Li  mi ri vi  mi ri 
p
Summing over all particle’s angular momentum about z axis
Lz   Li   mi ri 2 
i
i
Since I is constant for a rigid body
Thus the torque-angular momentum
relationship becomes
What do
you see?
Lz 
ext
2
i i
i
dL z
d
 I
dt
dt

 m r   I
 I
 is angular
acceleration
dLz

 I
dt
Thus the net external torque acting on a rigid body rotating about a fixed axis is equal to the moment
of inertia about that axis multiplied by the object’s angular acceleration with respect to that axis.
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
12
Example for Rigid Body Angular Momentum
A rigid rod of mass M and length l is pivoted without friction at its center. Two particles of mass
m1 and m2 are attached to either end of the rod. The combination rotates on a vertical plane with
an angular speed of . Find an expression for the magnitude of the angular momentum.
y
m2
l
q
m2 g
O
m1
m1 g
x
The moment of inertia of this system is
1
1
1
2
2

I

I

I

Ml

m
l

m2l 2
I
rod
m1
m2
1
12
4
4
2
l2  1
 L  I  l  1 M  m  m 
  M  m1  m2 

1
2
4
3


4 3

Find an expression for the magnitude of the angular acceleration of the
system when the rod makes an angle q with the horizon.
If m1 = m2, no angular
momentum because net
torque is 0.
If q//, at equilibrium
so no angular momentum.
Tuesday, June 26, 2007
First compute net
external torque
   m1 g
l
cosq
2
 ext     2

 2  m2 g
l
cosq
2
gl cosq m1  m2 
2
1
 m1  m2  gl cosq
2  m1  m2  cos q g
2



Thus 
ext
 2

1
 l
l 1

I
M

m

m
 M  m1  m2 

1
2 
becomesPHYS 1443-001, Summer 2006
3
4 3
13 

Dr. Jaehoon Yu
Conservation of Angular Momentum
Remember under what condition the linear momentum is conserved?
dp
F

0

Linear momentum is conserved when the net external force is 0. 
dt
p  const
By the same token, the angular momentum of a system
is constant in both magnitude and direction, if the
resultant external torque acting on the system is 0.
What does this mean?
dL


0
 ext
dt
L  const
Angular momentum of the system before and
after a certain change is the same.
r
r
Li  L f  constant
Three important conservation laws K i  U i  K f  U f
r
r
for isolated system that does not get p

p
i
f
affected by external forces
r
r
Li  L f
Tuesday, June 26, 2007
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
Mechanical Energy
Linear Momentum
Angular Momentum
14
Example for Angular Momentum Conservation
A star rotates with a period of 30 days about an axis through its center. After the star
undergoes a supernova explosion, the stellar core, which had a radius of 1.0x104km, collapses
into a neutron star of radius 3.0km. Determine the period of rotation of the neutron star.
What is your guess about the answer?
Let’s make some assumptions:
The period will be significantly shorter,
because its radius got smaller.
1. There is no external torque acting on it
2. The shape remains spherical
3. Its mass remains constant
Li  L f
Using angular momentum
conservation
I i  I f  f
The angular speed of the star with the period T is
Thus

I i
mri 2 2


f
If
mrf2 Ti
Tf 
2
f
 r f2
 2
r
 i
Tuesday, June 26, 2007
2

T
2

3
.
0


6
Ti  

2
.
7

10
days  0.23s

30
days

4

1
.
0

10



PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
15
Similarity Between Linear and Rotational Motions
All physical quantities in linear and rotational motions show striking similarity.
Quantities
Mass
Length of motion
Speed
Acceleration
Force
Work
Power
Momentum
Kinetic Energy
Tuesday, June 26, 2007
Linear
Mass
Rotational
Moment of Inertia
M
Distance
r
t
v
a
t
I  mr 2
Angle q (Radian)
L
q
t


t
v

Force F  ma
r r
Work W  F  d
Torque   I
Work W  q
P  
P  F v
p  mv
Kinetic
K
1
mv 2
2
L  I
Rotational
PHYS 1443-001, Summer 2006
Dr. Jaehoon Yu
KR 
1
I 2
2
16