* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lecture5
Planets beyond Neptune wikipedia , lookup
IAU definition of planet wikipedia , lookup
Kepler (spacecraft) wikipedia , lookup
Geocentric model wikipedia , lookup
Definition of planet wikipedia , lookup
Lunar theory wikipedia , lookup
Formation and evolution of the Solar System wikipedia , lookup
Dialogue Concerning the Two Chief World Systems wikipedia , lookup
History of Solar System formation and evolution hypotheses wikipedia , lookup
Philosophiæ Naturalis Principia Mathematica wikipedia , lookup
Astronomical unit wikipedia , lookup
Timeline of astronomy wikipedia , lookup
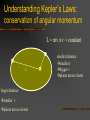
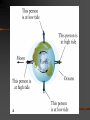
Lecture 5: Gravity and Motion Describing Motion and Forces speed, velocity and acceleration momentum and force mass and weight Newton’s Laws of Motion conservation of momentum analogs for rotational motion Torque and Angular Momentum A torque is a twisting force Torque = force x length of lever arm Angular momentum is torque times velocity For circular motion, L=mxvxr Laws for Rotational Motion Analogs of all of Newton’s Laws exist for rotational motion For example, in the absence of a net torque, the total angular momentum of a system remains constant There is also a Law of Conservation of Angular Momentum Conservation of Angular Momentum during star formation Newton’s Universal Law of Gravitation Every mass attracts every other mass through a force called gravity The force is proportional to the product of the two objects’ masses The force is inversely proportional to the square of the distance between the objects’ centers Universal Law of Gravitation The Gravitational Constant G The value of the constant G in Newton’s formula has been measured to be G = 6.67 x 10 –11 m3/(kg s2) This constant is believed to have the same value everywhere in the Universe Remember Kepler’s Laws? Orbits of planets are ellipses, with the Sun at one focus Planets sweep out equal areas in equal amounts of time Period-distance relation: (orbital period)2 = (average distance)3 Kepler’s Laws are just a special case of Newton’s Laws! Newton explained Kepler’s Laws by solving the law of Universal Gravitation and the law of Motion Ellipses are one possible solution, but there are others (parabolas and hyperbolas) Conic Sections Bound and Unbound Orbits Unbound (comet) Unbound (galaxy-galaxy) Bound (planets, binary stars) Understanding Kepler’s Laws: conservation of angular momentum L = mv x r = constant r larger distance smaller v planet moves slower smaller distance smaller r bigger v planet moves faster Understanding Kepler’s Third Law Newton’s generalization of Kepler’s Third Law is given by: 4p2 a3 p2 = G(M1 + M2) Mplanet << Msun, so 4p2 a3 p2 = GMsun This has two amazing implications: The orbital period of a planet depends only on its distance from the sun, and this is true whenever M1 << M2 An Astronaut and the Space Shuttle have the same orbit! Second Amazing Implication: If we know the period p and the average distance of the orbit a, we can calculate the mass of the sun! Example: Io is one of the large Galilean moons orbiting Jupiter. It orbits at a distance of 421,600 km from the center of Jupiter and has an orbital period of 1.77 days. How can we use this information to find the mass of the Sun? Tides The Moon’s Tidal Forces on the Earth Tidal Friction Synchronous Rotation Galactic Tidal Forces