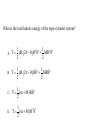* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Week 6
Mean field particle methods wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Particle filter wikipedia , lookup
Double-slit experiment wikipedia , lookup
Gibbs paradox wikipedia , lookup
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
Fundamental interaction wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Center of mass wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Classical mechanics wikipedia , lookup
Grand canonical ensemble wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Brownian motion wikipedia , lookup
Identical particles wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Work (physics) wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Atomic theory wikipedia , lookup
Physics 3210 Week 6 clicker questions In central-force motion, the areal velocity is a constant What is the period t of an elliptical orbit with area A? A. B. t A t A 2 C. t A D. t 2 A Area=A 2 Kepler’s First Law states that planets move in elliptical orbits with the sun at one focus. Why is the sun at one focus of the orbit? Because... A. Otherwise the planets wouldn’t all be in the same orbital plane. B. In two-body central-force motion one mass is always at the focus on the orbit. C. In two-body central-force motion the center of mass is always at the focus of the orbit, and the center of mass position is approximately given by the position of the sun. D. The moon is at the other focus. Sun A system of n particles is described by the masses and positions of each particle: m , r M m What is the position of the center of mass R of the system? 1 A. R r M 1 B. R m M C. R m r D. R Mr E. 1 R mr M Consider particles and b, and the internal force fb=the force on particle due to particle b. How does Newton’s third law relate the internal forces? A. fb fb B. fb fb C. fb fb D. fb fb 0 E. fb fb 1 fb b Suppose a system of particles experiences only internal forces (no external forces). What can you say about the momentum of the system? A. Nothing – having no external forces doesn’t determine the momentum of the system. B. The momentum of each particle is constant. C. The momentum of some (but not all) of the particles is constant. D. The momentum of the center of mass of the system is constant. Physics 3210 Wednesday clicker questions A chain with length b and mass density r is initially attached at both ends. One end of the chain is cut. After this falling end has moved down a distance x, what is the mass of the right (falling) side of the chain? r A. m right b x 2 r B. m right b x 2 C. m right r b x D. m right r b x E. mright rb x A chain with length b and mass density r is initially attached at both ends. One end of the chain is cut; the other end of the chain experiences a tension T. As the chain falls, what is the total external force on the chain (in the x direction)? A. FT B. F Mg C. F Mg T D. F Mg T x A chain with length b and mass density r is initially attached at both ends. The height is measured by x (increasing down) and the potential energy is zero at the attachment point. What is the total potential energy of the chain? A. U rgb B. U rgb rgb 2 C. U 2 2 r gb D. U 2 2 rgb E. U 4 x A system of n particles is described by the masses and positions of each particle, relative to the center of mass: m , r What can you say about the quantity A. m r 0 B. m r 0 D. m r 0 C. m r m r the position of the CM ? Physics 3210 Friday clicker questions Consider particles and b; the internal force fb=the force on particle due to particle b; the position vector rb= the vector from particle to particle b. If the force between the two particles is central, what can you say about rbfb? A. Nothing. B. rb fb 0 C. rb fb 0 D. rb fb 0 rb b A system of n particles is described by the masses and positions of each particle, relative to the center of mass: m , r The squared velocity of each particle is therefore v 2 r2 2r R R 2 v2 2r R V 2 What is the total kinetic energy of the system? 1 1 2 1 T m v m v V MV 2 2 2 2 1 1 2 2 B. T m v m v V MV 2 2 1 1 C. T m v2 MV 2 2 2 1 2 T m v V D. 2 A. The work done in unwrapping a rope from a cylinder is given by R x W rg x R sin dx R 0 What is the total work done? 2 A. W rgR cos 1 2 2 B. W rgR 2 2 cos 1 2 C. W rgR 2 cos 2 2 cos 2 1 D. W rgR R 2 What is the total kinetic energy of the rope-cylinder system? 1 1 2 2 2 2 T r R 2 R MR A. 2 2 1 1 2 2 B. T rR 2 R MR 2 2 C. 1 T m M R2 2 1 2 2 D. T m M R 2