Download Sep 17 - BYU Physics and Astronomy

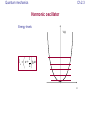
Physics 451 Quantum mechanics I Fall 2012 Sep 17, 2012 Karine Chesnel Quantum mechanics Announcements • Homework this week: Tuesday Sep 18 by 7pm: HW # 6 pb 2.10, 2.11, 2.12, 2.13, 2.14 Thursday Sep 20 by 7pm: HW # 7 pb 2.19, 2.20, 2.21, 2.22 • Monday: Review- Practice test Plan to work on your selected problem with your group and prepare the solution to be presented in class (~ 5 to 7 min) Quantum mechanics No student assigned to the following transmitters 17A79020 1E71A9C6 Please register your i-clicker at the class website! Quantum mechanics Ch 2.3 Harmonic oscillator V(x) Solving the Schrödinger equation: 1  2 2 p   m x    E  2m  Expressing the Hamiltonian a  in terms of convenient operators: 1  H    a a    2  or x 1 2m   ip  m x  1  H    a a    2  Quantum mechanics Ch 2.3 Harmonic oscillator Ladder operators: Raising operator: a n  n  1 n1 Lowering operator: a n  n n1 In this definition, the states  n are normalized a  n 1 a n  n1 En   En En   Quantum mechanics Quiz 8a What will be the final state of the particle after applying this operator? (ignore the coefficients) a a  a   a   n A.  n B.  n1 C.  n 2 D.  n1 E.  n 3 2 3 Quantum mechanics Ch 2.3 Harmonic oscillator Stationary states The ground state is given by the condition a 0  1  ip  m x  0  0 2m  m  m   2  0  x    e   1/4 Ground energy a 0  0 E0  1  2 x2 1 n n   a   0 n! 1  En   n    2  Quantum mechanics Ch 2.3 Harmonic oscillator Stationary states m  m   2  0  x    e   1/4 n  1 n  a   0 n! x2 The stationary states are orthonormal *   m n   nm Hermite polynomials Pb 2.10 Building  0  1 and  2 Checking the orthogonality Quantum mechanics Ch 2.3 Harmonic oscillator Energy levels V(x) 1  En   n    2  x Quantum mechanics Ch 2.3 Harmonic oscillator Expressing x, p and H in terms of ladder operators: a  1 2m   ip  m x  • Operator position x • Operator momentum pi • Operator Hamiltonian 2m m 2  a  a   a  a  1 1   H    a a      a a   2 2   Quantum mechanics Ch 2.3 Harmonic oscillator V(x) Expectation values x  a  2m   a  p i m 2 a  a   V  1  m 2 x 2  2 4 T  1 2  p  2m 4 ^   a  a   a  a  H   cn En n 1 2 2 2  x   a    a  2 2m  a    a  2 2m 2 2  a a  a a  a a  a a Pb 2.11, 2.12 Quantum mechanics Quiz 8b a  1 2m   ip  m x  Since the operators a+ and a- are shifting the stationary states from one level to another, and since the stationary states are all orthogonal, the expectations values for x and p on any state will ALWAYS be zero! A. True B. False Pb 2.13

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Top subcategories

Download Sep 17 - BYU Physics and Astronomy