Download Ian Walmsley

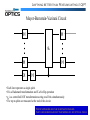
Engineering entanglement:
How and how much?
Alfred U’ren
Pablo Londero
Konrad Banaszek
Sascha Wallentowitz
Matt Anderson
Christophe Dorrer
Ian A. Walmsley
The Center for
Quantum
Information
Objectives
Develop “Quantum Toolbox” of elementary protocols
Determine resources needed for each element
Approaches
• Manipulating quantum fields
Engineering indistinguishability and entanglement
• Scaling issues for QIP readout based on experiment
Quantum field theoretic model of resources
Outcomes
• Developed engineered photon Sources
• Experimentally demonstrated resource scaling for
Interference-based information processing
A quantum computer
Input
Classical
information
Output
Classical
information
• Resources for preparing and reading register are important
The structure of quantum fields
Quantum field
ˆ () x,t    x,t aˆ
E


Size of computer

Mode function
Particle annihilation operator
Quantum state
 
   
 c n  
N
n 
Mode amplitude
 1
† n
a
vac
Number of
Particles
Vacuum
Quantum state characterized by classical and quantum parts
Field-theoretic view Provides a natural measure of resources
Detection of quantum systems via particle counting
Particle physics
Quantum Computation
Atomic physics
Optics
Generating Entangled States
Entangled state: multi-mode, multi-particle


1 † †
† ˆ†
 
aˆ1 aˆ 2  ˆa1
a2 vac
2
  ;  1,2,  ,
• N-particles
• 2N-modes (inc. hyper-entangled states)
• 2N pathways for creating particles in 2N modes
• Non-observed degrees of freedom must be identical
Classical mode structure
mode engineering:
Distinguishing information destroys interference
Braunstein-Mann Bell-state analyzer
Coincidence detection
implies input photons are
entangled
g
d
Bell-state measurements are a
requirement for teleportation, a
computational primitive
Classical mode structure
Even a single photon can have a complicated shape
e.g. localized in space and time
I (t )
 (t )
Time (fs)
Spectral density
Instantaneous power
t
2
2 
1
4
I ( )
 ( )
Wavelength (nm)
A. Baltuska et al, Opt. Lett. 23, 1474 (1998)
Generation of entangled photons
Spontaneous parametric downconversion generates pairs of
photons that may be entangled in frequency, time of emission and
polarization
Pulsed
pump
Signal photon
spectrum
s
p
i
Q
s
Idler photon
spectrum
Q
i
Type-I and II quasi-phase matching in
Nonlinear wave guides
Generation of entangled photons
 
 d d  
s
i
s
 i    s ,  i   s
Pump Envelope
SIGNAL
i
Product of
One-Photon
Fock States
Phase-Matching Function
s
s
i
IDLER
i
Generation of entangled photons
Supply two pathways for the generation of a pair of
photons with no distinguishing information in the
unmeasured degree of freedom
Interfering the two-photon state with itself
y
y
+
x
e i
x
BBO


Spectral entanglement is robust against decoherence
But Bell measurements difficult
Engineering the entropy of entanglement
Type II BBO, centered at 800nm (shows typical
spectral correlations present in SPDC.
Type II BBO, centered at 1600nm (note that
spectral correlations have been eliminated).
S=1.228
Type II ADP, centered at 800nm (note that
spectral correlations have been eliminated)
S=0
S=0
By appropriately choosing:
i) the crystal material
ii) the central wavelength
iii) the pump bandwidth
iv) the crystal length
it is possible to engineer a two-photon
state with zero spectral correlation.
Generating Correlated, unentangled photons
Why no entanglement?
How to attain positive correlation?
1. Dispersion cancellation to all orders:
Erdmann et al, Phys. Rev. A 62 53810 (2000)

System immune to
dispersion
2. Multiple-source experiments:
Grice, U’Ren at al, Phys. Rev. A 64 63815 (2001)
Spectral uncorrelation

Unwanted distinguishing
Information eliminated
Group velocity matching condition:
Rubin et al, Phys. Rev. A 56 1534 (1997)
KTP phase matching
function at 1.58mm:
KTP spectral
Intensity at 1.58mm:
Towards a useful source of heralded photons
Wave guide QPM downconversion
Compact NL structures
Low pump powers
Photons from independent sources
will interfere
High repetition rates
STP operation
Conditioned generation
Generating downconversion economically
Economy figure of merit:
GROUP
DOWNCOVERTER
PUMP
POWER
COUNTS
R
 Hz 


 mm  W 
Kwiat,
Steinberg [1]
Type-I 10cm
KDP crystal
10 mW
65 kHz
6.5  107
Weinfurter [2]
Type-II 2mm BBO
crystal
465mW
1250 kHz
2.7  106
Banaszek,
U’Ren,
Walmsley [3]
Type-I 1mm KTP
QPM waveguide
22mW
720 kHz
3.3  1010
[1] Kwiat et al, Phys. Rev. A 48 R867 (1993)
[2] Weinfurter et al, quant-ph/0101074 (2001)
[3] Banaszek, U’Ren et al, Opt. Lett. 26 1367 (2001)
Proposed Type II Polarization Entanglement Setup
FD: frequency doubler
SWP DICH: short-wave-pass
dichroic mirror
KTP II WG: waveguide
LWP DICH: long-wave-pass
dichroic mirror
PBS: polarizing beam splitter
POL1 and POL2: polarizers
DET1 and DET2: detectors




Applications to quantum-enhanced precision measurement
Accuracy doubling in phase measurement
using local entanglement only
No nonclassical light enters probed region enhanced accuracy for lossy systems
e.g. near-field microscopy
Possibility for efficient wave-based computation
Particles
Classical
Waves
Entangled
Particles
quantum
Computations based on
quantum interference
Science, January 2000
Scaling Criticisms
“Exponential overhead required for measurement”
Particle-counting readout
Definition of distinguishable detector modes
• Each state of the system mapped to a specific space-time mode
Equivalence of single-particle QIP and CWIP
Issues in single-particle quantum manipulation
• Single-particle systems do not scale poorly in readout
- Binary coding possible even for single particle systems
(No increase in number of detectors or particles required over
entangled register)
- No advantage to using several different degrees of freedom
• There’s nothing quantum about single particle processors
w/ counting readout, even using several degrees of freedom
• Collective manipulations on several particles cannot be made
efficiently through a single -particle degree of freedom
(implications for error-correcting protocols)
Anything better than Pentiums without QIP?
Meyer-Bernstein-Vazirani Circuit
H
H
ga
H
X
H
H
• Each line represents a single qubit.
• H is a Hadamard transformation and X a bit-flip operation
• ga is a controlled-NOT transformation acting on all bits simultaneously.
• The top n qubits are measured at the end of the circuit.
Since nowhere are the qubits entangled,
they can be replaced by the modes of an optical field.
Implications for atomic and molecular-based QIP
Database search
Ahn et al., Science (2000)
Graph connectivity analysis
Amitay et al., Chem. Phys. (2001)
Multilevel quantum simulator
Howell et al., PRA (2000)
CNOT gate
Tesch and De Vivie-Riedle, CPL (2001)
Coding
Particles
?
2Nx2N
?
NxN
NxN
• How to efficiently address the processor Hlibert space
using only one or two degrees of freedom?
2N
2N
2N
Non-orthogonal
orthogonal
Non-orthogonal
N ln2 N
(N)
N ln2 N
Summary: work to date
• New Methods developed for Generating entangled biphotons
• Model for resource analysis proposed based on experimental
realization
Resources for single-particle readout scaling
analyzed and experimentally verified
Plan: future work
• Develop waveguide sources as “entanglement factories”
• make use of low decoherence rates of spectrally
entangled biphotons
• Design classical implementation of MBV circuit
• Look at measures of nonclassicality based on scaling
associated with quantum logic