Download Louie de Broglie

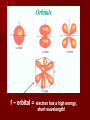
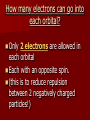
The Quantum Model of
the Atom
CP Chemistry
Louie de Broglie

Proposed that all particles of matter that
move exhibit wave like behavior (even a
baseball!)

He came up with the following equation that
relates the wavelength of a particle to its
mass and velocity. (Derived from E=mc2 and
E = hc/)

=
h_
mv
 Using the mass of an electron moving at the
speed of light, he calculated the same energy
level values as Bohr did for the Hydrogen atom.
Louis de Broglie

De Broglie realized that the
electrons exhibit wavelike
properties in their quantized
orbits. (draw pictures )
He said that if an electron has
wavelike motion and is
restricted to circular orbits of
a fixed radius, the electron
is allowed only certain
possible wavelengths,
frequencies and energies.
 Experiments did show that
electrons in atoms do exhibit
wave behavior with specific
frequencies.


Standing wave animation
The Heisenberg Uncertainty Principle
Heisenberg concluded that it is impossible to make
any measurement on an object without disturbing
it – at least a little.
 Electrons are detected by photons and because a
photon and an electron have the same energy,
any attempt to locate an electron with a photon
will knock the electron off course.
 Therefore:
It is impossible to know both the
position and the velocity of an electron at
the same time.



So we can only talk about the probability of
finding and electron in certain area (remember the
fuzzy cloud!)
Erwin Schrodinger

Used the idea that electrons behave like
waves to write and solve a mathematical
equation to describe the location and energy
of an electron in the hydrogen atom.

The modern description of the electron
cloud in atoms comes from the solutions to
the Schrodinger equation.

This equation showed that the energy of
electrons are restricted to certain
values.
Erwin Schrodinger
However, the equation does not define
the exact path the electron takes
around the nucleus.
 It only estimates the probability of
finding an electron in a certain position,
unlike Bohr’s circular orbits.

Electrons exist in regions called Orbitals
 Orbital – 3 dimensional cloud shape
around the nucleus that indicates the
probable location of an electron

Atomic Orbitals
 The
solutions to the Schrodinger
equation are called Quantum
Numbers, and they are used to
describe the properties, such as
the energy level and shape (s,
p, d or f), and Orientation of
the atomic orbitals.
“s” - orbital
• Each orbital’s
shape is
determined by
it’s the electron’s
energy, which is
related to its
wavelength!!!!!
“p” orbitals
An Electron in a p orbital has a different
wavelength and therefore a different
energy. This gives it a different shape!.
“d” orbitals
f – orbital = electron has a high energy,
short wavelength!
How many electrons can go into
each orbital?
 Only
2 electrons are allowed in
each orbital
 Each with an opposite spin.
 (this is to reduce repulsion
between 2 negatively charged
particles!)
Quantum # and Atomic Structure
Main
Energy
Level (n)
Sublevels
(n)
*Orbital
shapes
# of
orbitals
per
sublevel
1
s
2
s
p
1
3
3
s
p
d
1
3
5
4
s
p
d
f
1
3
5
7
1
# orbitals
per main
energy
level (n2)
# of
electrons
per
sublevel
Total # of
electrons
per main
energy
level (2n2)
1
2
2
4
s= 2
p= 6
8
9
s= 2
p=6
d = 10
18
16
s=2
p=6
d = 10
f = 14
32