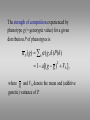Download Frequency-Dependent Selection on a Polygenic Trait

Sasha Gimelfarb
died on May 11, 2004
A Multilocus Analysis of
Frequency-Dependent Selection
on a Quantitative Trait
Reinhard Bürger
Department of Mathematics, University of Vienna
Frequency-dependent selection
has been invoked in the explanation of evolutionary
phenomena such as
•
•
•
•
Evolution of behavioral traits
Maintenance of high levels of genetic variation
Ecological character divergence
Reproductive isolation and sympatric speciation
Frequency-Dependent
Selection Caused by
Intraspecific Competition
Intraspecific competition mediated by a
quantitative trait under stabilizing selection:
•
•
•
•
•
•
•
•
Bulmer (1974, 1980)
Slatkin (1979, 1984)
Christiansen & Loeschcke (1980), Loeschcke & Christiansen (1984)
Clarke et al (1988), Mani et al (1990)
Doebeli (1996), Dieckmann & Doebeli (1999)
Matessi, Gimelfarb, & Gavrilets (2001)
Bolnick & Doebeli (2003)
Bürger (2002a,b), Bürger & Gimelfarb (2004)
The General Model
•
A randomly mating, diploid population with discrete
generations and equivalent sexes is considered.
•
Its size is large enough that random genetic drift can
be ignored.
•
•
Viability selection acts on a quantitative trait.
Environmental effects are ignored (in particular,
GxE interaction). Therefore, the genotypic value can
be identified with the phenotype.
Ecological Assumptions
Fitness is determined by two components:
•
by stabilizing selection on a quantitative trait,
S ( g )  1  s( g   ) 2 ,
and
•
by competition among individuals of similar trait value,
 ( g , h)  1  a( g  h) .
2
The strength of competition experienced by
phenotype g (= genotypic value) for a given
distribution P of phenotypes is
 P ( g )  h  ( g , h ) P ( h )
 1  a[( g  g )  VA ],
2
where g and VA denote the mean and (additive
genetic) variance of P.
If stabilizing selection acts independently of
competition, the fitness of an individual with
phenotype g can be written as
W ( g )  F ( N P ( g )) S ( g ),
where F(N) describes population growth according
to N´=NF(N). (F may be as in the discrete logistic,
the Ricker, the Beverton-Holt, the Hassell, or the
Maynard Smith model.)
For weak selection (O( s 2 )  0 , f = a/s constant),
this fitness function is approximated by
W ( g )  F ( N )(1  s( g   ) 2
 s ( N )[( g  g ) 2  VA ]),
where  (N ) is a compound measure for the strength
of frequency and density dependence relative to
'( N )
stabilizing selection, i.e.,  ( N )   NF
f .
F(N )
Genetic Assumptions
•
The trait is determined by additive contributions
from n diploid loci, i.e., there is neither dominance
nor epistasis.
•
At each locus there are two alleles. The allelic
effects at locus i are -gi/2 and gi/2. (This is
general because the scaling constants can be
absorbed by the position of the optimum and the
strength of selection.)
Genetical and Ecological Dynamics
pi , pi´ : frequencies of gamete i in consecutive generations
Wjk :
fitness of zygote consisting of gametes j, k
R(jk->i): probability that a jk-individual produces a
gamete of type i through recombination
W :
mean fitness
pi '  W
1
W
jk
p j pk R( jk  i )
j ,k
N '  NW
Issues and problems to be addressed
•
What aspects of genetics and what aspects of
ecology are relevant, and under what conditions?
•
When does FDS have important consequences for
the genetic structure of a population?
•
•
How does FDS affect the genetic structure?
How much genetic variation is maintained by this
kind of FDS?
Numerical Results from a
Statistical Approach
(with A. Gimelfarb)
Figure, poly, th=0
4.0
n = 2, = 0
n = 3, = 0
n = 4, = 0
3.5
Polymorphism
3.0
2.5
2.0
1.5
1.0
0.5
0.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
Strength of frequency dependence, f
2.2
2.4
Figure, poly,
th=0, 0.75
4.0
n = 2, = 0
n = 3, = 0
n = 4, = 0
n = 2, = 0.25
n = 3,  = 0.25
n = 4,  = 0.25
3.5
Polymorphism
3.0
2.5
2.0
1.5
1.0
0.5
0.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.8
2.0
Strength of frequency dependence, f
2.2
2.4
4.0
Figure:
poly
n = 2, r = 0.5
n = 3, r = 0.5
n = 4, r = 0.5
n = 2, 0 < r < 0.01
n = 3, 0 < r < 0.01
n = 4, 0 < r < 0.01
3.5
Polymorphism
3.0
2.5
2.0
1.5
1.0
0.5
0.0
0.0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
Strength of frequency dependence, f
Selection:
Quad. App.:
Stabilizing
Complicated
Disruptive
1.8
The Weak-Selection
or
Linkage-Equilibrium
Approximation
•
•
•
•
The structure is the same as in Turelli and Barton
2004 (but vi   ). The proofs of the results below
use their results.
The population is assumed to be in demographic
equilibrium, i.e., N and η are treated as constants.
All models of intraspecific competition and
stabilizing selection I know have the above
differential equation as their weak-selection
approximation.
‘Arbitrary‘ population regulation, i.e., with a
unique stable carrying capacity, is admitted.
General Conclusions
•
The amount and properties of variation
maintained depend in a nearly threshold-like
way on , the strength of frequency and
density dependence relative to stabilizing
selection.
•
This critical value is independent of the number
of loci and, apparently, also of the linkage map.
Weak FDS
•
If more than two loci contribute to the trait, then
weak frequency dependence ( < 1) can maintain
significantly more genetic variance than pure
stabilizing selection, but still not much. The more
loci, the larger this effect.
•
FDS of such strength does not induce a qualitative
change in the equilibrium structure relative to pure
stabilizing selection.
•
Such FDS does not lead to disruptive selection,
rather, stabilizing selection prevails.
Strong FDS
•
Strong FDS ( > 1) causes a qualitative change
in the genetic structure of a population by
inducing highly polymorphic equilibria in positive
linkage disequilibrium.
•
In parallel, such FDS induces strong disruptive
selection, the fitness differences between
phenotypes maintained in the population being
much larger than under pure stabilizing selection.
Disruptive Selection
•
Therefore, disruptive selection should be easy to
detect empirically whenever FDS is strong enough
to affect the equilibrium structure qualitatively.
•
Its strength (the curvature of the fitness function at
equilibrium) is s( – 1).
When Genetics Matters
•
•
•
The degree of polymorphism maintained by strong
FDS depends on the number of loci and the
distribution of their effects.
Models based on popular symmetry assumptions,
such as equal locus effects or symmetric selection, are
often not representative (they maintain more
polymorphism).
Linkage becomes important only if tight. It produces
clustering of the phenotypic distribution. Otherwise,
the LE-approximation does a very good job.
Outlook
•
Include assortative mating to study the conditions
leading to divergence within a population (work in
progress  K. Schneider).
•
Determine the conditions under which sympatric
speciation is induced by intraspecific competition.