* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Diagnostics of complex plasmas using a dust grains
Aharonov–Bohm effect wikipedia , lookup
Weakly-interacting massive particles wikipedia , lookup
Future Circular Collider wikipedia , lookup
ALICE experiment wikipedia , lookup
Strangeness production wikipedia , lookup
Double-slit experiment wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Standard Model wikipedia , lookup
ATLAS experiment wikipedia , lookup
Identical particles wikipedia , lookup
Electron scattering wikipedia , lookup
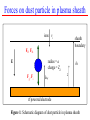
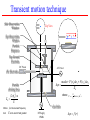
TEST GRAINS AS A NOVEL DIAGNOSTIC TOOL B.W. James, A.A. Samarian and W. Tsang School of Physics, University of Sydney NSW 2006, Australia [email protected] ICPP Sydney 2002 What is a dusty plasma? • a low temperature plasma containing small particles of diameters in nanometer and micrometer range • particles acquire a net negative charge (at equilibrium floating potential) • particles levitated in sheaths where electric force balances gravity • particles can form liquid- and solid- like arrays (plasma or Coulomb crystal) which can undergo phase transitions Forces on dust particle in plasma sheath ions vi sheath boundary FE, Fth E radius = a charge = Zd Fg, Fi heq hb z rf powered electrode Figure 1: Schematic diagram of dust particle in plasma sheath Forces on a dust particle • Electric force • Gravity force • Ion drag force FE Zd E 4 3 Fg a g 3 eZ 2 2 d Fi a nimiv i 1 2 amivi • Thermophoretic force 32 m 2 T Fth a 15 8T z where – a is particle radius – is particle density – Zde is charge on particle – mi is ion mass – ni is ion density – vi in ion velocity in sheath – Te is electron temperature – T is gas temperature – m is mass of gas atoms – is thermal conductivity of plasma Experimental arrangement Figure 2: Experimental chamber and image of test dust particles levitated above the electrode. The test grains are generated in the discharge (power up to 200W, pressure up to 1 torr) by electrode sputtering. Equilibrium position of dust particle Using the force balance equation, FE + Fg + Fi + Fth = 0 the equilibrium position has been calculated as a function of radius a (see figure 3) using following assumptions – – – – – – Vs ~ 60 V, linear variation of electric field in sheath vi from sheath model Te ~ 2 eV R = 2 g cm-3 dT/dz ~ 1-5 K cm-1 (varying with input power) Zd calculated from OML theory Equilibrium position vs. radius wi = 106 s-1 (dashed) 5x106 s-1 (dotted), 107 s-1 (solid), 0,5 (h b -h eq )/h b 0,4 0,3 0,2 0,1 0 0 0,5 1 1,5 2 2,5 3 Dust radius, m Figure 3: Equilibrium height of dust particles above electrode heq, relative to height of sheath boundary hb as a function particles radius for several values of ion plasma frequency, wi 4nie2 / mi Alternative estimates of sheath width T, eV I, a.u. 3 1 heq 2,5 2 0.5 1,5 1 0,5 0 0 2 4 6 8 10 12 14 16 18 20 h, mm Figure 4: Electron temperature Te (points with error bars) measured using Langmuir probe; discharge emission (solid line); the dashed line shows the equilibrium position (heq =10.8 mm) of test grains (a~350 nm). Discharge conditions: p = 90m Torr, P = 80 W. Sheath width as function of pressure h b (mm) Position of sheath edge (hb) vs pressure at different rf-input powers 30 – 35W 25 – 60W 20 – 100W 15 10 5 0 0 10 20 30 40 50 60 70 80 90 100 Pressure (mTorr) Visualisation of rf sheath • Sufficiently small particles cannot achieve force equilibrium in the sheath - the sheath becomes a particle-free region • Particles occupy pre-sheath and positive column • Provides a visualisation of the sheath-plasma boundary - see Figure 5 QuickTime™ and a Photo - JPEG decompressor are needed to see this picture. Figure 5: The shape of the potential well above the confining electrode in a radio-frequency (rf) discharge with a printed-circuit board electrode system (Cheung et al., 2002) was visualised using fine dust grains that were generated in the discharge. The well shape was found to depend strongly on the confining potential Transient motion technique Side Observation Window Top View Top Observation Window Particle Dispenser Top Ground Electrode DC Power AC Power Pin Electrodes a v1 Particle Driving Pad (2f 0 ) 2 m ZD E' Where And mas F (v1 )s1 F (v2 )s2 Zd where 4 F mnn vTn a 2 v 3 Gas Inlet f 0 is the resonant frequency E 'is the electric field gradient v2 s1 s2 RF Supply 15MHz f (r ) Effect of hot electrons in sheath h heq Rd ~ h heq Figure 6: Square root of distance of particle from sheath edge as a function of particle radius Particle Data Probe Data Figure 7: Potential profile measured by a Langmuir probe, and by transient motion analysis Conclusions • as particle radius decreases, equilibrium position moves closer to edge of sheath • sufficiently small particles avoid sheath region, occupying presheath and positive column. providing visualisation of sheath • hot electrons affect equilibrium position • potential and electric filed profiles determined from transient motion analysis Acknowledgements This work is supported by the Australian Research Council and the Science Foundation for Physics within the University of Sydney References A.A. Samarian and B.W. James, Phys Letters A, 287 (2001) 125 F. Cheung, A. Samarian and B. James, Physica Scripta, T98 (2002) 143-5 Particle Data Probe Data Figure 8: Radial electric field derived from results in figure 7. Least Mean Square Fit for Particle Data Least Mean Square Fit for Probe Data