* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lesson 1-3
Law of large numbers wikipedia , lookup
Ethnomathematics wikipedia , lookup
Positional notation wikipedia , lookup
Foundations of mathematics wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Infinitesimal wikipedia , lookup
Bernoulli number wikipedia , lookup
Fundamental theorem of algebra wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Non-standard analysis wikipedia , lookup
Surreal number wikipedia , lookup
Location arithmetic wikipedia , lookup
Large numbers wikipedia , lookup
Hyperreal number wikipedia , lookup
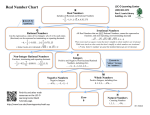
Notes for Lesson 1-3: Real Numbers and the Number Line Vocabulary: Square root - A number that is multiplied by itself to form a product Radicand – The expression under the radical sign Radical – An expression made up of a radical symbol and a radicand Perfect square - A number whose positive square root is a whole number 1 - Finding the square roots of perfect squares Example: Find the square root √81 = 9 𝑏𝑒𝑐𝑎𝑢𝑠𝑒 92 = 81 9 √ 16 = 3 4 √169 = 13 3 9 4 16 𝑏𝑒𝑐𝑎𝑢𝑠𝑒 ( )2 = √2.25 = 1.5 Square roots of many numbers are not whole numbers, like the square root of 15. However, we can use the square roots of perfect squares to estimate the square roots of other numbers. 15 32 9 and 42 16 15 is closer to 16 Do √34 and √386 3.9 15.21 and 3.8 14.44 2 2 So the 15 is closer to 3.9 2 - Application Nancy wants to plant a garden in a square shaped plot. She has enough vegetables to cover 19 sq. ft. Estimate to the nearest tenth the length of the side of the square plot she can plant. 3 - Classifying Real Numbers Vocabulary: Set – A well-defined collection of objects Element of a Set – A member of a set Subset – A set consisting of elements from the given set Natural numbers - The counting numbers Whole Numbers - The natural numbers and zero (numbers that represent the amount of something) Integers - Whole numbers and their opposites a Rational numbers - Numbers that can be expressed as a fraction b a Irrational numbers - Numbers that cannot be expressed as a fraction b Real numbers - The set of all rational and irrational numbers Examples: Classifying real numbers 8 belongs to which sets of real numbers 9 answer: rational 18 belongs to which sets of real numbers answer: natural, whole, integer, rational 20 belongs to which sets of real numbers answer: irrational 4 belongs to which sets of real numbers 9 6 belongs to which sets of real numbers 7 answer: rational answer: integers, rationals 4 – Comparing real numbers and graphing them on a number line. Vocabulary: Inequality – A mathematical sentence that compares the values of two expressions Using > < ≥ ≤ to compare the values of two numbers. 1 Compare √18 𝑎𝑛𝑑 4 3 Compare √129 𝑎𝑛𝑑 11.2 5 – Graphing and Ordering Real Numbers 2 What is the order of √4, 0.4, − 3 , √2, 𝑎𝑛𝑑 − 1.5 from least to greatest -1.5 -2/3 √2 0.4 7 What is the order of 3.5, −2.1, √9, − 2 , 𝑎𝑛𝑑 √5 from least to greatest. -7/2 -2.1 √5 3.5