Download Lecture 1

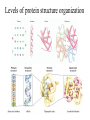
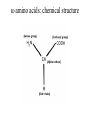
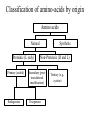
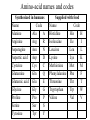
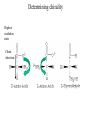
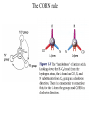
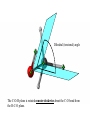
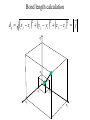
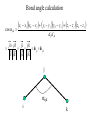
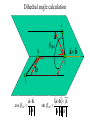
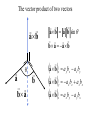
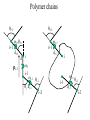
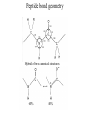
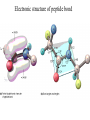
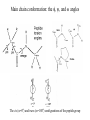
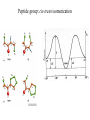
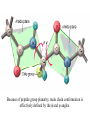
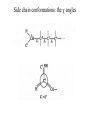
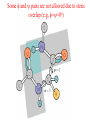
Protein Structure and Energetics
Adam Liwo
Room B325
Faculty of Chemistry, University of Gdańsk
phone: 58 523 5124 (or 5124 within the University)
email: [email protected]
[email protected]
Course language: English
Schedule and requirements
• Mondays, 8:15 – 10:00, room C209, Faculty
of Chemistry, University of Gdańsk
• 2 problem sets
• Final exam
Scope of this course
1. Levels of structural organization of proteins.
2. Quantitative description of protein geometry.
3. Secondary and supersecondary structure.
4. Tertiary and quaternary structure.
5. Schemes of protein-structure classification.
6. Interactions in proteins and their interplay.
7. Folding transition as a phase transition.
8. Foldability and the necessary conditions for foldability.
9. Misfolding and aggregation; formation of amyloids.
10. Experimental methods for the investigation of protein folding.
11. Atomistic-detailed and coarse-grained models and force fields
for protein simulations.
Literature
• C. Branden, J. Toze, „Introduction to Proten Structure”,
Garland Publishing,1999
• G. E. Schultz, R.H., Schrimer, „Principles of Protein
Structure”, Springer-Verlag, 1978
• Ed. J. Twardowski, „Biospektroskopia”, cz. I, PWN, 1989
• I. Z. Siemion, „Biostereochemia”, PWN, 1985
Proteins: history of view
• 1828: By syntesizing urea, Friedrich Woehler voided the vis
vitalis theory, opening roads to modern organic chemistry.
• 1850’s: First amino acids isolated from natural products
• 1903-1906: By hydrolysis of natural proteins, Emil Fischer
proves that they are copolymers of amino acids (strange, but
none of his so fundamental papers earned more than ~60
citations!).
• 1930’s and 1940’s: proteins are viewed as spheroidal particles
which form colloidal solution; their shape is described in terms
of the long-to-short axis ratio.
• 1930’s: it is observed that denaturated proteins do not
crystallize and change their physicochemical and spectral
properties.
Proteins: history of view (continued)
• 1940’s: evidence from X-ray accumulates suggesting that
fibrous proteins such as silk and keratin might have regular
structure.
• 1951: Pauling, Corey, and Branson publish the theoretical
model of protein helical structures.
• 1960: Laskowski and Scheraga discover anomalous pKa
values in ribonuclease, which suggest that the acidbase
groups are shielded from the solvent to different extent.
• 1963: First low-resolution X-ray structure of a protein
(horse hemoglobin) published by the Perutz group.
• Today: 68840 structures of proteins, nucleic acids, and
sugars in the Protein Data Bank.
Protein shapes from viscosity data
a
b
Polson, Nature, 740, 1936
Pauling’s model of helical structures
First structure: hemoglobin (X-ray)
Example of a recently solved structure: DnaK chaperone from E.coli (2KHO)
Levels of protein structure organization
The primary structure (Emil Fischer, 1904)
C-terminus
N-terminus
H3N+-Gly-Ile-Val-Cys-Glu-Gln-..........-Thr-Leu-His-Lys-Asn-COO-
a-amino acids are protein building blocks
a-amino acids: chemical structure
Classification of amino-acids by origin
Amino acids
Natural
Proteinic (L only)
Primary (coded)
Endogenous
Synthetic
Non-Proteinic (D and L)
Secondary (posttranslational
modification)
Exogenous
Tertiary (e.g.,
cystine)
Amino-acid names and codes
Synthesized in humans
Name
Code
Alanine
Ala
A
Arginine
Arg
R
Supplied with food
Name
Code
Histidine
His
H
Isoleucine
Ile
I
Asparagine
Aspartic acid
Cysteine
Asn
Asp
Cys
N
D
C
Leucine
Lysine
Methionine
Leu
Lys
Met
L
K
M
Glutamine
Glutamic acid
Glycine
Gln
Glu
Gly
Q
E
G
Phenylalanine
Threonine
Tryptophan
Phe
Thr
Trp
F
T
W
Proline
Serine
Tyrosine
Pro
Ser
Tyr
P
S
Y
Valine
Val
V
The peptide bond
Venn diagram of amino acid properties
The "Universal" Genetic Code
In form of codon, Left-Top-Right (ATG is Met)
T
Phe
T
C
A
G
Leu
Leu
Ile
C
Ser
Pro
Thr
A
Tyr
Ter
His
Gln
Asn
G
Cys
Ter
Trp
Arg
Ser
Met
Lys
Arg
Val
Asp
Glu
Gly
Ala
T
C
A
G
T
C
A
G
T
C
A
G
T
C
A
G
Atom symbols and numbering in amino acids
Chirality
Enantiomers
Phenomenological manifestation of chiraliy: optical dichroism (rotation
of the plane of polarized light).
Determining chirality
Highest
oxidation
state
Chain
direction
The CORN rule
Absolute configuration: R and S chirality
Rotate from „heaviest” to „lightest” substituent
R (D) amino acids
S (L) amino acids
Representation of geometry of molecular
systems
• Cartesian coordinates
• describe absolute geometry of a system,
• versatile with MD/minimizing energy,
• need a molecular graphics program to visualize.
• Internal coordinates
• describe local geometry of an atom wrt a selected reference
frame,
• with some experience, local geometry can be imagined
without a molecular graphics software,
• might cause problems when doing MD/minimizing energy
(curvilinear space).
Cartesian coordinate system
z
zH(6)
H(6)
O(2)
H(4)
Atom
C(1)
O(2)
H(3)
H(4)
H(5)
H(6)
x (Å)
0.000000
0.000000
1.026719
-0.513360
-0.513360
0.447834
y (Å)
0.000000
0.000000
0.000000
-0.889165
0.889165
0.775672
C(1)
yH(6)
x
xH(6)
H(5)
H(3)
y
z (Å)
0.000000
1.400000
-0.363000
-0.363000
-0.363000
1.716667
Internal coordinate system
H(6)
H(4)
i
C(1)
O(2)
H(3)
O(2) H(4)
H(5)
H(6)
1.40000
1.08900
1.08900
1.08900
0.95000
C(1)
H(5)
H(3)
aijk
dij
*
*
*
*
*
109.47100
109.47100
109.47100
109.47100
bijkl
j k l
1
*
1 2
* 120.00000 * 1 2 3
* -120.00000 * 1 2 3
* 180.00000 * 2 1 5
Bond length
Bond (valence) angle
Dihedral (torsional) angle
The C-O-H plane is rotated counterclockwise about the C-O bond from
the H-C-O plane.
Improper dihedral (torsional) angle
Bond length calculation
dij 
x
 xi   y j  yi   z j  zi   i j
2
j
2
2
zj
zi
xi
xj
yi
xj
Bond angle calculation
cos a ijk


x  x x

ji  jk
ji jk
i

j
ji
ji

jk
jk
k
 x j    yi  y j  yk  y j   zi  z j z k  z j 
d ij d jk
 uˆ ji  uˆ jk
j
aijk
i
k
Dihedral angle calculation

a
k
i
bijkl
 
ab

b
j
l
cos b ijkl
 
ab
 
ab
sin b ijkl


 
a  b  jk
 
a b jk
The vector product of two vectors
 
ab

a
q
 
ba

b
 
 
a  b  a b sin q
 
 
b  a  a  b






 
a  b x  a y bz  a z by
 
a  b y  a xbz  a z bx
 
a  b z  a x by  a y bx
  
i
j k
 
a  b  ax a y az 
bx by bz



i a y bz  a z by   ja x bz  a z bx   k a x by  a y bx 
Some useful vector identities
 
 
a  b  b  a
  
aa  0
       
  
a  b  c  ba  c   ca  b   a  b  c




aijk
k
i

a
180oaijk

a'
j
 
a  a'  ji
d ji

jk
a'  
ji cos180  a ijk  
cos a ijk jk
d jk
jk
d ji

a  ji 
cos a ijk jk
d jk

 
a  a  a  d 2ji 1  cos 2 a ijk  d ji sin a ijk



a
k
bijkl

b
l
d ji

a  ji 
cos a ijk jk
d jk

d
b  kl  kl cos a ijk kj
d jk
cos b ijkl
i
 
ab
j

a  d ji sin a ijk

b  d kl sin a ijk
ji  kl
 cos a ijk cos a jkl


d ij d kl
ab
  
sin a ijk sin a jkl
ab

a
bijkl
k

b
 
ab
j
l
cos b ijkl
 
ab
   
ab
sin b ijkl 
ji  kl
 cos a ijk cos a jkl
d ij d kl
sin a ijk sin a jkl
 ji  kl jk
d ij d jk d kl sin a ijk sin a jkl
Calculation of Cartesian coordinates in a local reference
frame from internal coordinates
H(5)
z
H(6)
d26
a426
C(1)
b3426
O(2)
y
x
H(4)
xH(6)  d 26 cos a 426
yH(6)  d 26 sin a 426 cos b 3426
z H(6)  d 26 sin a 426 sin b 3426
H(3)
Need to bring the coordinates to the
global coordinate system
local
i
i
i
 xiglobal   e11


x

e
e
i
21
31 

 


i
i
i
local
 yiglobal    e12

e22 e32  yi 
 global   i
i
i  local 
 zi
  e13 e23 e33  zi 




global
T
R
 E R local
Polymer chains
qi+2
qi+2
wi+1
wi+1qi+1
i+1
i+1
di+1
di
pi-1
i
di+1
i
wi
i-1
wi-1 q
i-1
qi di-1
i-2
wi-1
i-1
qi-1
di-1
i-2
r1  p 0
r2  p1  r1
r3  T1p 2  r2
r4  R1T2 T1p 3  r3

ri  R i 3Ti  2 R i  4 Ti 3  R1T2 T1p i 1  ri 1

rn 1  R n 3Tn  2 R n  4 Tn 3  R1T2 T1p n 1  rn 1
For regular polymers (when there are „blocks” inside such as in the right picture, pi
is a full translation vector and Ti-2Ri-1 is a full transformation matrix).
 di 
 
pi   0 
0 
 
 cos qi

Ti   sin qi
 0

 sin q i
cos q i
0
0

0
1 
0
1

R i   0 cos wi
 0 sin w
i

0 

 sin wi 
cos wi 
Peptide bond geometry
Hybrid of two canonical structures
60%
40%
Electronic structure of peptide bond
Peptide bond: planarity
The partially double
character of the peptide
bond results in
•planarity of peptide
groups
•their relatively large
dipole moment
Main chain conformation: the f, y, and w angles
The cis (w=0o) and trans (w=180o) configurations of the peptide group
Peptide group: cis-trans isomerization
Skan z wykresem energii
Because of peptide group planarity, main chain conformation is
effectively defined by the f and y angles.
Side chain conformations: the c angles
The dihedral angles with which to describe
the geometry of disulfide bridges
Some f and y pairs are not allowed due to steric
overlap (e.g, f=y=0o)
The Ramachandran map