* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 1
Ancestral sequence reconstruction wikipedia , lookup
G protein–coupled receptor wikipedia , lookup
Magnesium transporter wikipedia , lookup
Point mutation wikipedia , lookup
Expression vector wikipedia , lookup
Interactome wikipedia , lookup
Amino acid synthesis wikipedia , lookup
Biosynthesis wikipedia , lookup
Homology modeling wikipedia , lookup
Genetic code wikipedia , lookup
Peptide synthesis wikipedia , lookup
Western blot wikipedia , lookup
Metalloprotein wikipedia , lookup
Two-hybrid screening wikipedia , lookup
Protein–protein interaction wikipedia , lookup
Ribosomally synthesized and post-translationally modified peptides wikipedia , lookup
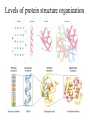
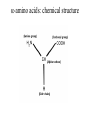
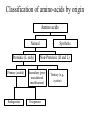
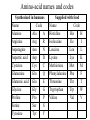
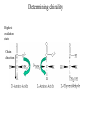
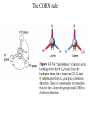
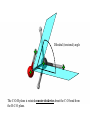
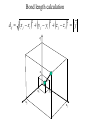
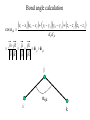
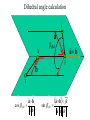
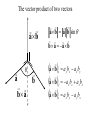
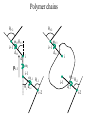
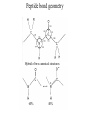
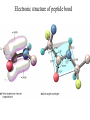
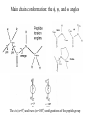
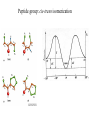
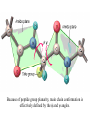
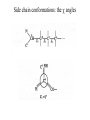
Protein Structure and Energetics Adam Liwo Room B325 Faculty of Chemistry, University of Gdańsk phone: 58 523 5124 (or 5124 within the University) email: [email protected] [email protected] Course language: English Schedule and requirements • Mondays, 8:15 – 10:00, room C209, Faculty of Chemistry, University of Gdańsk • 2 problem sets • Final exam Scope of this course 1. Levels of structural organization of proteins. 2. Quantitative description of protein geometry. 3. Secondary and supersecondary structure. 4. Tertiary and quaternary structure. 5. Schemes of protein-structure classification. 6. Interactions in proteins and their interplay. 7. Folding transition as a phase transition. 8. Foldability and the necessary conditions for foldability. 9. Misfolding and aggregation; formation of amyloids. 10. Experimental methods for the investigation of protein folding. 11. Atomistic-detailed and coarse-grained models and force fields for protein simulations. Literature • C. Branden, J. Toze, „Introduction to Proten Structure”, Garland Publishing,1999 • G. E. Schultz, R.H., Schrimer, „Principles of Protein Structure”, Springer-Verlag, 1978 • Ed. J. Twardowski, „Biospektroskopia”, cz. I, PWN, 1989 • I. Z. Siemion, „Biostereochemia”, PWN, 1985 Proteins: history of view • 1828: By syntesizing urea, Friedrich Woehler voided the vis vitalis theory, opening roads to modern organic chemistry. • 1850’s: First amino acids isolated from natural products • 1903-1906: By hydrolysis of natural proteins, Emil Fischer proves that they are copolymers of amino acids (strange, but none of his so fundamental papers earned more than ~60 citations!). • 1930’s and 1940’s: proteins are viewed as spheroidal particles which form colloidal solution; their shape is described in terms of the long-to-short axis ratio. • 1930’s: it is observed that denaturated proteins do not crystallize and change their physicochemical and spectral properties. Proteins: history of view (continued) • 1940’s: evidence from X-ray accumulates suggesting that fibrous proteins such as silk and keratin might have regular structure. • 1951: Pauling, Corey, and Branson publish the theoretical model of protein helical structures. • 1960: Laskowski and Scheraga discover anomalous pKa values in ribonuclease, which suggest that the acidbase groups are shielded from the solvent to different extent. • 1963: First low-resolution X-ray structure of a protein (horse hemoglobin) published by the Perutz group. • Today: 68840 structures of proteins, nucleic acids, and sugars in the Protein Data Bank. Protein shapes from viscosity data a b Polson, Nature, 740, 1936 Pauling’s model of helical structures First structure: hemoglobin (X-ray) Example of a recently solved structure: DnaK chaperone from E.coli (2KHO) Levels of protein structure organization The primary structure (Emil Fischer, 1904) C-terminus N-terminus H3N+-Gly-Ile-Val-Cys-Glu-Gln-..........-Thr-Leu-His-Lys-Asn-COO- a-amino acids are protein building blocks a-amino acids: chemical structure Classification of amino-acids by origin Amino acids Natural Proteinic (L only) Primary (coded) Endogenous Synthetic Non-Proteinic (D and L) Secondary (posttranslational modification) Exogenous Tertiary (e.g., cystine) Amino-acid names and codes Synthesized in humans Name Code Alanine Ala A Arginine Arg R Supplied with food Name Code Histidine His H Isoleucine Ile I Asparagine Aspartic acid Cysteine Asn Asp Cys N D C Leucine Lysine Methionine Leu Lys Met L K M Glutamine Glutamic acid Glycine Gln Glu Gly Q E G Phenylalanine Threonine Tryptophan Phe Thr Trp F T W Proline Serine Tyrosine Pro Ser Tyr P S Y Valine Val V The peptide bond Venn diagram of amino acid properties The "Universal" Genetic Code In form of codon, Left-Top-Right (ATG is Met) T Phe T C A G Leu Leu Ile C Ser Pro Thr A Tyr Ter His Gln Asn G Cys Ter Trp Arg Ser Met Lys Arg Val Asp Glu Gly Ala T C A G T C A G T C A G T C A G Atom symbols and numbering in amino acids Chirality Enantiomers Phenomenological manifestation of chiraliy: optical dichroism (rotation of the plane of polarized light). Determining chirality Highest oxidation state Chain direction The CORN rule Absolute configuration: R and S chirality Rotate from „heaviest” to „lightest” substituent R (D) amino acids S (L) amino acids Representation of geometry of molecular systems • Cartesian coordinates • describe absolute geometry of a system, • versatile with MD/minimizing energy, • need a molecular graphics program to visualize. • Internal coordinates • describe local geometry of an atom wrt a selected reference frame, • with some experience, local geometry can be imagined without a molecular graphics software, • might cause problems when doing MD/minimizing energy (curvilinear space). Cartesian coordinate system z zH(6) H(6) O(2) H(4) Atom C(1) O(2) H(3) H(4) H(5) H(6) x (Å) 0.000000 0.000000 1.026719 -0.513360 -0.513360 0.447834 y (Å) 0.000000 0.000000 0.000000 -0.889165 0.889165 0.775672 C(1) yH(6) x xH(6) H(5) H(3) y z (Å) 0.000000 1.400000 -0.363000 -0.363000 -0.363000 1.716667 Internal coordinate system H(6) H(4) i C(1) O(2) H(3) O(2) H(4) H(5) H(6) 1.40000 1.08900 1.08900 1.08900 0.95000 C(1) H(5) H(3) aijk dij * * * * * 109.47100 109.47100 109.47100 109.47100 bijkl j k l 1 * 1 2 * 120.00000 * 1 2 3 * -120.00000 * 1 2 3 * 180.00000 * 2 1 5 Bond length Bond (valence) angle Dihedral (torsional) angle The C-O-H plane is rotated counterclockwise about the C-O bond from the H-C-O plane. Improper dihedral (torsional) angle Bond length calculation dij x xi y j yi z j zi i j 2 j 2 2 zj zi xi xj yi xj Bond angle calculation cos a ijk x x x ji jk ji jk i j ji ji jk jk k x j yi y j yk y j zi z j z k z j d ij d jk uˆ ji uˆ jk j aijk i k Dihedral angle calculation a k i bijkl ab b j l cos b ijkl ab ab sin b ijkl a b jk a b jk The vector product of two vectors ab a q ba b a b a b sin q b a a b a b x a y bz a z by a b y a xbz a z bx a b z a x by a y bx i j k a b ax a y az bx by bz i a y bz a z by ja x bz a z bx k a x by a y bx Some useful vector identities a b b a aa 0 a b c ba c ca b a b c aijk k i a 180oaijk a' j a a' ji d ji jk a' ji cos180 a ijk cos a ijk jk d jk jk d ji a ji cos a ijk jk d jk a a a d 2ji 1 cos 2 a ijk d ji sin a ijk a k bijkl b l d ji a ji cos a ijk jk d jk d b kl kl cos a ijk kj d jk cos b ijkl i ab j a d ji sin a ijk b d kl sin a ijk ji kl cos a ijk cos a jkl d ij d kl ab sin a ijk sin a jkl ab a bijkl k b ab j l cos b ijkl ab ab sin b ijkl ji kl cos a ijk cos a jkl d ij d kl sin a ijk sin a jkl ji kl jk d ij d jk d kl sin a ijk sin a jkl Calculation of Cartesian coordinates in a local reference frame from internal coordinates H(5) z H(6) d26 a426 C(1) b3426 O(2) y x H(4) xH(6) d 26 cos a 426 yH(6) d 26 sin a 426 cos b 3426 z H(6) d 26 sin a 426 sin b 3426 H(3) Need to bring the coordinates to the global coordinate system local i i i xiglobal e11 x e e i 21 31 i i i local yiglobal e12 e22 e32 yi global i i i local zi e13 e23 e33 zi global T R E R local Polymer chains qi+2 qi+2 wi+1 wi+1qi+1 i+1 i+1 di+1 di pi-1 i di+1 i wi i-1 wi-1 q i-1 qi di-1 i-2 wi-1 i-1 qi-1 di-1 i-2 r1 p 0 r2 p1 r1 r3 T1p 2 r2 r4 R1T2 T1p 3 r3 ri R i 3Ti 2 R i 4 Ti 3 R1T2 T1p i 1 ri 1 rn 1 R n 3Tn 2 R n 4 Tn 3 R1T2 T1p n 1 rn 1 For regular polymers (when there are „blocks” inside such as in the right picture, pi is a full translation vector and Ti-2Ri-1 is a full transformation matrix). di pi 0 0 cos qi Ti sin qi 0 sin q i cos q i 0 0 0 1 0 1 R i 0 cos wi 0 sin w i 0 sin wi cos wi Peptide bond geometry Hybrid of two canonical structures 60% 40% Electronic structure of peptide bond Peptide bond: planarity The partially double character of the peptide bond results in •planarity of peptide groups •their relatively large dipole moment Main chain conformation: the f, y, and w angles The cis (w=0o) and trans (w=180o) configurations of the peptide group Peptide group: cis-trans isomerization Skan z wykresem energii Because of peptide group planarity, main chain conformation is effectively defined by the f and y angles. Side chain conformations: the c angles The dihedral angles with which to describe the geometry of disulfide bridges Some f and y pairs are not allowed due to steric overlap (e.g, f=y=0o) The Ramachandran map