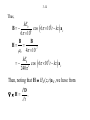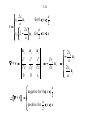* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Module 3 - University of Illinois Urbana
Speed of gravity wikipedia , lookup
History of quantum field theory wikipedia , lookup
Noether's theorem wikipedia , lookup
Magnetic field wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Equations of motion wikipedia , lookup
Magnetic monopole wikipedia , lookup
Kaluza–Klein theory wikipedia , lookup
Superconductivity wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Electromagnet wikipedia , lookup
Electromagnetism wikipedia , lookup
Electrostatics wikipedia , lookup
Field (physics) wikipedia , lookup
Partial differential equation wikipedia , lookup
Time in physics wikipedia , lookup
Fundamentals of Electromagnetics: A Two-Week, 8-Day, Intensive Course for Training Faculty in Electrical-, Electronics-, Communication-, and Computer- Related Engineering Departments by Nannapaneni Narayana Rao Edward C. Jordan Professor Emeritus of Electrical and Computer Engineering University of Illinois at Urbana-Champaign, USA Distinguished Amrita Professor of Engineering Amrita Vishwa Vidyapeetham, India Amrita Viswa Vidya Peetham, Coimbatore August 11, 12, 13, 14, 18, 19, 20, and 21, 2008 3-1 Module 3 Maxwell’s Equations In Differential Form Faraday’s law and Ampere’s Circuital Law Gauss’ Laws and the Continuity Equation Curl and Divergence 3-2 Instructional Objectives 8. Determine if a given time-varying electric/magnetic field satisfies Maxwell’s curl equations, and if so find the corresponding magnetic/electric field, and any required condition, if the field is incompletely specified 9. Find the electric/magnetic field due to onedimensional static charge/current distribution using Maxwell’s divergence/curl equation for the electric/magnetic field 10. Establish the physical realizability of a static electric field by using Maxwell’s curl equation for the static case, and of a magnetic field by using the Maxwell’s divergence equation for the magnetic field 3-3 Faraday’s Law and Ampère’s Circuital Law (FEME, Secs. 3.1, 3.2; EEE6E, Sec. 3.1) 3-4 Maxwell’s Equations in Differential Form Why differential form? Because for integral forms to be useful, an a priori knowledge of the behavior of the field to be computed is necessary. The problem is similar to the following: If 1 0 y(x) dx 2, what is y(x)? There is no unique solution to this. 3-5 However, if, e.g., y(x) = Cx, then we can find y(x), since then 1 x 2 1 0 Cx dx 2 or C 2 0 2 or C 4 y(x) 4x. On the other hand, suppose we have the following problem: dy If 2, what is y? dx Then y(x) = 2x + C. Thus the solution is unique to within a constant. 3-6 FARADAY’S LAW First consider the special case E Ex (z,t) a x and H H y (z, t) a y and apply the integral form to the rectangular path shown, in the limit that the rectangle shrinks to a point. y z (x, z) x z (x, z + z) S C (x + x, z) (x + x, z + z) x 3-7 d C E d l dt S B dS Ex z z E Lim x z z x 0 z 0 d By x z x Ex z x x, z dt Ex z x x z Lim x 0 z 0 By Ex z t B dt d y x, z x z x z 3-8 General Case E Ex (x, y, z,t)a x Ey (x, y, z,t)a y Ez (x, y, z, t)a z H H x (x, y, z,t)a x H y (x, y, z,t)a y Hz (x, y, z, t)a z Ez E y Bx – – y z t By E x Ez – – z x t Ey Ex Bz – – x y t Lateral space derivatives of the components of E Time derivatives of the components of B 3-9 Combining into a single differential equation, ax ay az x y B – z t Ex Ey Ez B E– t Differential form of Faraday’s Law ax ay az x y z B Del Cross E or Curl of E = – t 3-10 AMPÈRE’S CIRCUITAL LAW Consider the general case first. Then noting that d C E • dl – dt S B • dS E – (B) we obtain from analogy, t d C H • dl S J • dS dt S D • dS H J (D) t 3-11 D HJ t Thus Special case: E Ex (z,t)a x , H H y (z,t)a y ax ay az 0 0 0 Hy D J z t 0 Hy Dx – Jx z t Differential form of Ampère’s circuital law 3-12 Hy Dx – Jx – z t Ex. For E E0 cos 6 ×10 t kz a y 8 in free space 0 , 0 , J = 0 , find the value(s) of k such that E satisfies both of Maxwell’s curl equations. Noting that E Ey (z,t)a y , we have from B E– , t 3-13 ay az B – E – 0 t 0 z 0 Ey 0 ax Bx Ey t z 8 E cos 6 10 t kz 0 z kE0 sin 6 108 t kz kE0 8 Bx cos 6 10 t kz 8 6 10 3-14 Thus, kE0 8 B cos 6 10 t kz ax 8 6 10 B B H 0 4 107 kE0 8 cos 6 10 t kz ax 2 240 Then, noting that H H x (z,t)a x , we have from D H , t 3-15 ax ay az D ×H 0 t 0 z Hx 0 0 Dy H x t z 2 k E0 8 sin 6 10 t kz 2 240 3-16 2 k E0 8 Dy cos 6 10 t kz 3 8 1440 10 k 2 E0 8 D cos 6 10 t kz a y 3 8 1440 10 D D E 9 0 10 36 k 2 E0 8 cos 6 10 t kz a y 2 4 3-17 Comparing with the original given E, we have k 2 E0 E0 4 2 k 2 E E0 cos 6 108 t 2 z a y Sinusoidal traveling waves in free space, propagating in the z directions with velocity, 3 108 ( c) m s. 3-18 Gauss’ Laws and the Continuity Equation (FEME, Secs. 3.4, 3.5, 3.6; EEE6E, Sec. 3.2) 3-19 GAUSS’ LAW FOR THE ELECTRIC FIELD S D • dS V dv z (x, y, z) x Dx xx y z Dx x y z Dy z x Dy z x y y y Dz z z x y Dz z x y x y z z y y x 3-20 D x x x Dx x y z Dy Dy Δ z Δ x y +Δy y Lim x 0 y 0 z 0 Lim x 0 y 0 z 0 Dz z z Dz z x y x y z x y z x y z 3-21 Dx Dy Dz x y z Longitudinal derivatives of the components of D •D Divergence of D = Ex. Given that 0 for – a x a 0 otherwise Find D everywhere. 3-22 • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • 0 x=–a x=0 x=a Noting that = (x) and hence D = D(x), we set 0 and 0, so that y z Dx Dy Dz Dx • D x y z x 3-23 Thus, • D = gives Dx (x) x which also means that D has only an xcomponent. Proceeding further, we have x Dx – x dx C where C is the constant of integration. Evaluating the integral graphically, we have the following: 3-24 –a 0 a x x – ( x) dx 2 0 a –a 0 0 a x From symmetry considerations, the fields on the two sides of the charge distribution must be equal in magnitude and opposite in direction. Hence, C = – 0a 3-25 Dx 0 a –a a – 0a 0 a a x for x a D 0 x a x for a x a a a for x a x 0 x 3-26 GAUSS’ LAW FOR THE MAGNETIC FIELD S D • dS = V dv • D From analogy S B • dS = 0 = V 0 dv •B0 •B0 Solenoidal property of magnetic field lines. Provides test for physical realizability of a given vector field as a magnetic field. 3-27 LAW OF CONSERVATION OF CHARGE d dv 0 J • dS S dt V • J t ( ) 0 • J 0 t Continuity Equation 3-28 SUMMARY B E– t D HJ t •D (1) (2) (3) •B0 (4) •J 0 t (5) (4) is, however, not independent of (1), and (3) can be derived from (2) with the aid of (5). 3-29 Curl and Divergence (FEME, Secs. 3.3, 3.6; EEE6E, Sec. 3.3) 3-30 Maxwell’s Equations in Differential Form B ×E = t D ×H = J t D B ax ay az Curl × Α x y z Ax Ay Az Divergence A= Ax A y Az x y z 3-31 Basic definition of curl Lim C A d l an ×A = S 0 S max × A is the maximum value of circulation of A per unit area in the limit that the area shrinks to the point. Direction of ×A is the direction of the normal vector to the area in the limit that the area shrinks to the point, and in the right-hand sense. 3-32 Curl Meter is a device to probe the field for studying the curl of the field. It responds to the circulation of the field. 3-33 3-34 a 2x for 0 x v0 a az 2 v 2x a v0 2 az for x a a 2 ax ay az ×v x y z 0 vz 0 × v y vz ay x a negative for 0 x 2 positive for a x a 2 2v0 a a y 2v0 a y a 3-35 Basic definition of divergence A A v 0 Lim dS v is the outward flux of A per unit volume in the limit that the volume shrinks to the point. Divergence meter is a device to probe the field for studying the divergence of the field. It responds to the closed surface integral of the vector field. 3-36 x Example: At the point (1, 1, 0) (a) x 1 2 ax Divergence zero (b) 1 y 1 ay y z x 1 1 Divergence positive y z x (c) x a y y 1 1 Divergence negative y z 1 3-37 Two Useful Theorems: Stokes’ theorem C A d l = × A dS S Divergence theorem S A dS = V A useful identity ×A A dv 3-38 ax ay az ×Α x y z Ax Ay Az ×A = × A x × A y × A z x y z x y z 0 x y z Ax Ay Az The End