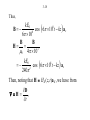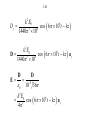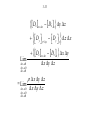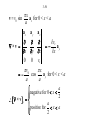Download PPT - University of Illinois Urbana

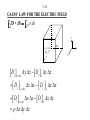
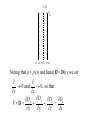
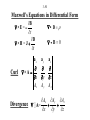
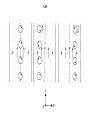
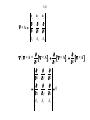
Fundamentals of Electromagnetics
for Teaching and Learning:
A Two-Week Intensive Course for Faculty in
Electrical-, Electronics-, Communication-, and
Computer- Related Engineering Departments in
Engineering Colleges in India
by
Nannapaneni Narayana Rao
Edward C. Jordan Professor Emeritus
of Electrical and Computer Engineering
University of Illinois at Urbana-Champaign, USA
Distinguished Amrita Professor of Engineering
Amrita Vishwa Vidyapeetham, India
Program for Hyderabad Area and Andhra Pradesh Faculty
Sponsored by IEEE Hyderabad Section, IETE Hyderabad
Center, and Vasavi College of Engineering
IETE Conference Hall, Osmania University Campus
Hyderabad, Andhra Pradesh
June 3 – June 11, 2009
Workshop for Master Trainer Faculty Sponsored by
IUCEE (Indo-US Coalition for Engineering Education)
Infosys Campus, Mysore, Karnataka
June 22 – July 3, 2009
3-2
Module 3
Maxwell’s Equations
in Differential Form
3.1 Faraday’s law and Ampere’s Circuital Law
3.2 Gauss’ Laws and the Continuity Equation
3.3 Curl and Divergence
3-3
Instructional Objectives
16. Obtain the simplified forms of Faraday’s law and
Ampere’s circuital law in differential forms for any
special cases of electric and magnetic fields, respectively,
or the particular differential equation that satisfies both
laws for a special case of electric or magnetic field
17. Determine if a given time-varying electric/magnetic field
satisfies Maxwell’s curl equations, and if so find the
corresponding magnetic/electric field, and any required
condition, if the field is incompletely specified
18. Find the magnetic field due to one-dimensional static
current distribution using Maxwell’s curl equation for the
magnetic field
19. Find the electric field due to one-dimensional static
charge distribution using Maxwell’s divergence equation
for the electric field
3-4
Instructional Objectives (Continued)
20. Establish the physical realizability of a static electric field
by using Maxwell’s curl equation for the static case, and
of a magnetic field by using the Maxwell’s divergence
equation for the magnetic field
21. Investigate qualitatively the curl and divergence of a
vector field by using the curl meter and divergence meter
concepts, respectively
22. Apply Stokes’ and divergence theorems in carrying out
vector calculus manipulations
3-5
3.1 Faraday’s Law and
Ampère’s Circuital Law
(EEE, Sec. 3.1; FEME, Secs. 3.1, 3.2)
3-6
Maxwell’s Equations in Differential Form
Why differential form?
Because for integral forms to be useful, an a priori
knowledge of the behavior of the field to be
computed is necessary.
The problem is similar to the following:
If
1
0 y(x) dx  2, what is y(x)?
There is no unique solution to this.
3-7
However, if, e.g., y(x) = Cx, then we can find y(x),
since then
1
2
1
x 
0 Cx dx  2 or C  2 0  2 or C  4
 y  x   4x
On the other hand, suppose we have the following
problem:
dy
If
 2, what is y?
dx
Then y(x) = 2x + C
Thus the solution is unique to within a constant.
3-8
FARADAY’S LAW
First consider the special case
E  Ex ( z , t ) a x and H  Hy ( z,t ) a y
and apply the integral form to the rectangular path
shown, in the limit that the rectangle shrinks to a
point.
y
z
(x, z)
x
z (x, z + z)
S
C
(x + x, z) (x + x, z + z)
x
3-9
d
C E d l   dt S B dS


d
 Ex z  z x   Ex z x    By  x, z x z
dt
E 

Lim
x z  z
x 0
z 0

  Ex z x
x z
 Lim
x 0
z 0
By
Ex

z
t
 B 

dt
d
y
x, z

x z
x z
3-10
General Case
E  Ex (x, y, z,t)a x  Ey (x, y, z,t)a y  Ez (x, y, z, t)a z
H  H x (x, y, z,t)a x  H y (x, y, z,t)a y  Hz (x, y, z, t)a z
d  x, y, z   z 
c  x , y  y , z   z 
z
e  x   x, y , z   z 
x
f  x   x, y , z 
z
a  x, y , z 
y
b  x, y  y , z 
y
x
g  x   x, y  y , z 
3-11
E  Ex (x, y, z,t)a x  Ey (x, y, z,t)a y  Ez (x, y, z, t)a z
H  H x (x, y, z,t)a x  H y (x, y, z,t)a y  Hz (x, y, z, t)a z
E y
Ez
Bx
–
–
y
z
t
By
Ez
E x
–
–
z
x
t
E y
Bz
E x
–
–
x
y
t
Lateral space
derivatives of the
components of E
Time derivatives of
the components of B
3-12
The terms on the left sides are the net right-lateral
differentials of pairs of components of E. For
example, in the first equation, it is the net rightlateral differential of Ey and Ez normal to the xdirection. The figure below illustrates (a) the case of
zero value, and (b) the case of nonzero value, for this
quantity.
Ey
x×
Ey
y
Ez
Ez
Ez
Ez
z
Ey
Ey
(a)
(b)
3-13
Combining into a single differential equation,
ax

x
Ex
ay

y
Ey
az

B
–
z
t
Ez
B
×E–
t
Differential form
of Faraday’s Law



  ax
 ay
 az
x
y
z
B
Del Cross E or Curl of E = –
t
3-14
AMPÈRE’S CIRCUITAL LAW
Consider the general case first. Then noting that
d
C E • dl  – dt S B • dS
  E  –  (B)
we obtain from analogy,
t
d
C H • dl  S J • dS  dt S D • dS
  H  J   (D)
t
3-15
D
×HJ
t
Thus
Special case:
E  Ex (z,t)a x , H  H y (z,t)a y
ax
ay
0
0
0
Hy
H y
az

D
J
z
t
0
Dx
–
 Jx 
z
t
Differential form
of Ampère’s
circuital law
3-16
H y
Dx
 – Jx –
z
t


E3.1 For E  E0 cos 6 ×108 t  kz a y
in free space    0 ,   0 , J = 0 ,
find the value(s) of k such that E satisfies both
of Maxwell’s curl equations.
Noting that E  Ey (z,t)a y , we have from
B
E–
,
t
3-17
ax
B
 –  E  – 0
t
0
ay
0
Ey
az

z
0
Bx Ey

t
z

  E0 cos  6 108 t  kz  
z
 kE0 sin  6 108 t  kz 
kE0
8
Bx  
cos
6


10
t  kz 

8
6 10
3-18
Thus,
kE0
8
B
cos  6 10 t  kz  ax
8
6 10
B
B
H

0 4 107
kE0
8

cos
6


10
t  kz  ax

2
240
Then, noting that H  H x (z,t)a x , we have from
D
H
,
t
3-19
ax
D
 ×H  0
t
Hx
ay
0
0
az

z
0
 Dy
 Hx

t
z
k 2 E0
8

sin  6  10 t  kz 
2
240
3-20
2
k E0
8
Dy 
cos  6  10 t  kz 
3
8
1440  10
2
k E0
8
D
cos
6


10
t  kz  a y

3
8
1440  10
D
D
E
 9
0 10 36
k 2 E0
8

cos
6


10
t  kz  a y

2
4
3-21
Comparing with the original given E, we have
k 2 E0
E0 
4 2
k   2
E  E0 cos  6  108 t  2 z  a y
Sinusoidal traveling waves in free space, propagating in the
z directions with velocity, 3  108 ( c) m s.
3-22
E3.2.
3-23
3-24
Review Questions
3.1. Discuss the applicability of integral forms of Maxwell’s
equations versus that of the differential forms for
obtaining the solutions for the fields.
3.2. State Faraday’s law in differential form for the special
case of E = Ex(z, t)ax and H = Hy(z, t)ay . How is it
derived from Faraday’s law in integral form?
3.3. How would you derive Faraday’s law in differential form
from its integral form for the general case of an arbitrary
electric field?
3.4. What is meant by the net right-lateral differential of the
x- and y- components of a vector normal to the zdirection? Give an example in which the net right-lateral
differential of Ex and Ey normal to the z-direction is
zero, although the individual derivatives are nonzero.
3.5. What is the determinant expansion for the curl of a vector
in Cartesian coordinates?
3-25
Review Questions (Continued)
3.6. State Ampere’s circuital law in differential form for the
general case of an arbitrary magnetic field. How is it
obtained from its integral form?
3.7. State Ampere’s circuital law in differential form for the
special case of H = Hy(z, t)ay . How is it derived from the
Ampere’s circuital law for the general case in differential
form?
3.8. If a pair of E and B at a point satisfies Faraday’s law in
differential form, does it necessarily follow that it also
satisfies Ampere’s circuital form and vice versa?
3.9. Discuss the determination of magnetic field for one
dimensional current distributions, in the static case, using
Ampere’s circuital law in differential form, without the
displacement current density term.
3-26
Problem S3.1. Obtaining the differential equation for a
special case that satisfies both of Maxwell’s curl equations
3-27
Problem S3.2. Finding possible condition for a specified
field to satisfy both of Maxwell’s curl equations
3-28
Problem S3.3. Magnetic field due to a one-dimensional
current distribution for the static case
3-29
Problem S3.3. Magnetic field due to a one-dimensional
current distribution for the static case (Continued)
3-30
Problem S3.3. Magnetic field due to a one-dimensional
current distribution for the static case (Continued)
3-31
3.2 Gauss’ Laws and
the Continuity Equation
(EEE, Sec. 3.2; FEME, Secs. 3.4, 3.5, 3.6)
3-32
GAUSS’ LAW FOR THE ELECTRIC FIELD
S D • dS  V  dv
z
(x, y, z)
x
z
y
 Dx xx y z   Dx x y z
  Dy 
y y
z x   Dy  z x
y
  Dz z z x y   Dz z x y
  x y z
y
x
3-33
 D 

x x x

  Dx x y  z

  Dy 
  Dy  Δ z Δ x
y +Δy
y
Lim
x 0
y 0
z 0
 Lim
x  0
y  0
z  0
  Dz z z   Dz z   x y
 x y  z
  x y  z
 x y  z
3-34
Dy Dz
Dx



x
y
z
Longitudinal derivatives
of the components of D
The quantity on the left side is the net longitudinal
differential of the components of D, that is, the
algebraic sum of the derivatives of components of D
along their respective directions. It can be written as
 D, which is known as the “divergence of D.”
Thus, the equation becomes
•D 
3-35
The figure below illustrates the case of (a) zero value,
and (b) nonzero value for  D .
Dy
Dy
z
Dz
x
y
Dx
Dx
Dz
Dy
(a)
E3.3 Given that
0 for – a  x  a
  
0 otherwise
Find D everywhere.
Dz
Dx
Dx
Dz
Dy
(b)
3-36
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

0
x=–a x=0 x=a
Noting that  = (x) and hence D = D(x), we set


 0 and
 0, so that
y
z
Dy
Dz
Dx
Dx
• D 



x
y
z
x
3-37
Thus,  • D =  gives
Dx
  ( x)
x
which also means that D has only an xcomponent. Proceeding further, we have
Dx     x  dx  C
x

where C is the constant of integration.
Evaluating the integral graphically, we have the
following:
3-38

–a
0
a
x
x
–   ( x) dx
2 0 a
–a
0
0
a
x
From symmetry considerations, the fields on
the two sides of the charge distribution must
be equal in magnitude and opposite in
direction. Hence,
C = –  0a
3-39
Dx
0 a
–a
a
– 0a
 0 a a x for x  a

D   0 x a x for  a  x  a
  a a for x  a
 0 x
x
3-40
GAUSS’ LAW FOR THE MAGNETIC FIELD
S D • dS = V  dv
• D  
From analogy
S B • dS = 0 = V 0
dv
•B0
•B0
Solenoidal property of magnetic field lines. Provides test for
physical realizability of a given vector field as a magnetic
field.
3-41
LAW OF CONSERVATION OF CHARGE
d  dv  0
J
•
dS

S
dt V
 • J  t (  )  0

• J 
  0
t
Continuity
Equation
3-42
SUMMARY
B
E–
t
D
HJ
t
•D
•B0

•J
0
t
(1)
(2)
(3)
(4)
(5)
(4) is, however, not independent of (1), and (3) can
be derived from (2) with the aid of (5).
3-43
The interdependence of fields and sources
through Maxwell’s equations
+
J
H ,B
+
Law of Conservation
of Charge (5)

Gauss’ Law
for E (3)
Ampere’s
Circuital
Law (2)
Faraday’s
Law (1)
D,E
3-44
Review Questions
3.10. State Gauss’ law for the electric field in differential
form. How is it derived from its integral form?
3.11. What is meant by the net longitudinal differential of the
components of a vector field? Give an example in
which the net longitudinal differential of the
components of a vector field is zero, although the
individual derivatives are nonzero.
3.12. What is the expression for the divergence of a vector in
Cartesian coordinates?
3.13. Discuss the determination of electric field for one
dimensional charge distributions, in the static case,
using Gauss’ law for the electric field in differential
form.
3-45
Review Questions (Continued)
3.14. State Gauss’ law for the magnetic field in differential
form. How is it obtained from its integral form?
3.15. How can you determine if a given vector field can be
realized as a magnetic field?
3.16. State the continuity equation.
3.17. Summarize Maxwell’s equations in differential form
and the continuity equation, stating which of the
equations are independent.
3.18. Discuss the interdependence of fields and sources
through Maxwell’s equations.
3-46
Problem S3.4. Finding the electric field due to a onedimensional charge distribution for the static case
3-47
Problem S3.5. Finding the condition for the realizability
of a specified vector field as a certain type of field
3-48
Problem S3.6. Determination of the group belonging to a
specified vector field, based on its physical realizability
3-49
3.3 Curl and Divergence
(EEE, Sec. 3.3, App. B ; FEME, Secs. 3.3
and 3.6, App. B)
3-50
Maxwell’s Equations in Differential Form
B
×E = 
t
D
×H = J 
t
ax

Curl  × Α 
x
Ax
Divergence  A=
 D

ay

y
Ay
Ax
x
B0
az

z
Az

Ay
y

Az
z
3-51
Curl and Divergence in Cylindrical Coordinates
ar
r

 A=
r
Ar
a


rA
az
r

z
Az
1 
1 A Az
 A=
r Ar 

r r
r 
z


3-52
Curl and Divergence in Spherical Coordinates
ar
r 2sin 

 A=
r
Ar
a
r sin 
a
r


rA


r sin  A
1  2
1

 A= 2
r Ar 
A sin  

r sin  
r r
1 A

r sin  


3-53
Basic definition of curl
Lim   C A d l 

 an
×A =
S  0  S 

 max
 × A is the maximum value of circulation of A per
unit area in the limit that the area shrinks to the point.
Direction of  ×A is the direction of the normal
vector to the area in the limit that the area shrinks
to the point, and in the right-hand sense.
3-54
Curl Meter
is a device to probe the field for studying the curl of the
field. It responds to the circulation of the field.
E3.4
v  v0 sin
x
a
az for 0 < x < a
3-55
3-56
x
v  v0 sin
a
az for 0 < x < a
ax
ay
az

×v 
x
0

y
0

z
vz

   × v y
 v0
a
cos
x
a
vz

ay
x
a y for 0 < x < a
a

 negative for 0  x  2

 positive for a  x  a

2
3-57
Basic definition of divergence

A dS 
Lim  S

 A

v  0 
v


is the outward flux of A per unit volume in the limit that
the volume shrinks to the point.

Divergence meter
is a device to probe the field for studying the divergence
of the field. It responds to the closed surface integral of
the vector field.
3-58
Divergence positive for (a) and (b), negative for (c) and (d),
and zero for (e)
3-59
E 3.5
At the point (1, 1, 0)
(a)
 x  1
2
1
ax
Divergence zero
(b)
x
 y  1 ay
y
z
x
1
1
Divergence positive
y
z
x
y
(c) e
ay
1
1
Divergence negative
y
z
1
3-60
Two Useful Theorems:
Stokes’ theorem

C
A d l =   × A dS
S
Divergence theorem

S
A dS =
 
V
A useful identity
 ×A  
A  dv
3-61
ax
ay
az

×Α 
x
Ax

y
Ay

z
Az



 ×A =
 × A x   × A y   × A z
x
y
z

x


x
Ax

y

y
Ay

z

0
z
Az
3-62
Review Questions
3.19. State and briefly discuss the basic definition of the curl
of a vector.
3.20. What is a curl meter? How does it help visualize the
behavior of the curl of a vector field?
3.21. Provide two examples of physical phenomena in which
the curl of the vector field is nonzero.
3.22. State and briefly discuss the basic definition of the
divergence of a vector.
3.23. What is a divergence meter? How does it help visualize
the behavior of the divergence of a vector field?
3.24. Provide two examples of physical phenomena in which
the divergence of the vector field is nonzero.
3-63
Review Questions (Continued)
3.25. State Stokes’ theorem and discuss its application.
3.26. State the divergence theorem and discuss its application.
3.27. What is the divergence of the curl of a vector?
3-64
Problem S3.7. Investigation of the behavior of the curl of
a vector field for different cases
3-65
Problem S3.8. Investigation of the behavior of the
divergence of a vector field for different cases
3-66
Problem S3.9. Verification of Stokes’ theorem and an
application of the divergence theorem
3-67
Problem S3.9. Verification of Stokes’ theorem and an
application of the divergence theorem (Continued)
The End