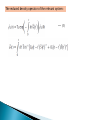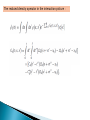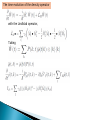* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PPT File
Bell's theorem wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Quantum computing wikipedia , lookup
Wave function wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Quantum field theory wikipedia , lookup
Coupled cluster wikipedia , lookup
Quantum teleportation wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Quantum machine learning wikipedia , lookup
Renormalization group wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
EPR paradox wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum group wikipedia , lookup
Quantum entanglement wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Scalar field theory wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Perturbation theory wikipedia , lookup
Quantum decoherence wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Schrödinger equation wikipedia , lookup
Hydrogen atom wikipedia , lookup
Path integral formulation wikipedia , lookup
Quantum state wikipedia , lookup
Hidden variable theory wikipedia , lookup
Coherent states wikipedia , lookup
Probability amplitude wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
History of quantum field theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Canonical quantization wikipedia , lookup
Dirac equation wikipedia , lookup
Ochanomizu Univ. F. Shibata (1) Brief historical survey Environment System (2) Reduced dynamics and the master equation of open quantum systems:M. Ban, S. Kitajima and F. S., Phys. Lett. A 374(2010) 2324. (3) Relaxation process of quantum system: B-K-S, Phys. Rev. A 82, (2010) 022111 Damping theory General formalism D and N Transport, diffusion W. Heitler (~1936) .. Schrodinger picture (SP) R. Kubo Explicitly cited in: Time-Convolution (TC) S. Nakajima (1958) R. Zwanzig (1960) “Micro-Langevin” H. Mori (1965) Several work on Time-Convolutionless(TCL) Relaxation and decoherence Cumulant expansion Heisenberg picture (HP) S-Takahashi -Hashitsume (1977) Expansion formulae SP & HP, TC & TCL R. Kubo (1963) van Kampen (1974) M. Tokuyama “Micro-Langevin” -H. Mori (1976) Chaturvedi-S (1979) S- Arimitsu (1980) Uchiyama-S (1999) Relevant Books: 1) H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems (2006, Oxford ) 2) F. S., T.Arimitsu, M.Ban and S.Kitajima, Physics of Quanta and Non-equilibrium Systems (2009, Univ. of Tokyo press, in Japanese) Phys. Lett. A 374 (2010) 2324 1. Reduced dynamics of an open quantum system Liouville-von Neumann equation Formal solution super operator Initial density operator of the total system : Unitary superoperator : The reduced density operator of the relevant system : The reduced density operator of the relevant system : ・・・ (1) 2. The master equation for the reduced density operator We can obtain up to the second order with respect to the interaction Formal solution ・・・ (2) where the time ordering is to be done as indicated by the subscript quantity G which is different from the time ordering With respect to S. The condition of the second order master equation to be exact is found by differentiating (1), It should be noted that the quantity G(t) can not be placed across the time-ordering symbol because of its time integral up to t . The condition of the second order equation becomes exact is given by ・・・ (3) which can be cast into the statement: The final necessary and sufficient condition for the second order master equation becomes exact is that the system operators S(t)’s are commutable each other at different times. 3. Reduced dynamics of the boson-detector model The reduced density operator of the propagating particle : ・・・ (4) (4) The reduced density operator in the interaction picture : References 1) R.P. Feynman, F.L. Vernon Jr., Ann. Phys. 24 (1963) 118. 2) A.O. Caldeira, A.J. Leggett, Physica A 121 (1983) 587. 3) H.-P. Breuer, F. Petruccione, Phys. Rev. A 63 (2001) 032102. 4) H.-P. Breuer, A. Ma, F. Petruccione, LANL, quant-ph/0209153, 2002; in: A. Leggett, B. Ruggiero, P. Silvestrini(Eds.), Quantum Computing and Quantum Bits in Mesoscopic Systems, Kluwer, New York, 2004, pp. 263-271. 5) A. Ishizaki, Y. Tanimura, Chem. Phys. 347 (2008) 185. Phys. Rev. A 82, (2010) 022111 1. Stochastic Liouville equation : (A) Time-evolution by stochastic Hamiltonian ((Time-evolution equation)) Formal solution Density operator averaged over the stochastic process Joint probability When there is no initial correlation between the quantum system and stochastic process, we obtain the time-convolutionless (TCL) quantum master equation (B) Time-evolution of joint density operator Time-evolution equation of the transition probability condition : Probability vector Time-evolution of the probability vector Time-evolution of the joint density operator ・・・ (5) Matrix form : The interaction picture The initial joint state The formal solution The differential operator The stochastic Liouville equation The reduced density operator The probability density function 2. Derivation from the quantum master equation : (A) General consideration The whole system is composed of the relevant quantum system and an interaction mode under the influence of a narrowing limit environment. Phys. Rev. A 82, (2010) 022111 The time evolution of the density operator with the Lindblad operator, Taking (B) Discrete stochastic variable The quantum master equation : (C) Continuous stochastic variable The quantum master equation The density operator The differential equation for the system operator The differential equation for the system operator The time evolution equation of the joint density operator 3. Reduced dynamics with initial correlation : (A) General formulation A qubit state is represented by The characteristic function of the stochastic variable The coherence of a qubit is characterized by For a two-qubit system A and B, The two-qubit Hamiltonian in the interaction picture: The reduced density operator of the two-qubit system: (B) Gauss-Markov process The time evolution of coherence for the Gauss-Markov fluctuation for the slow (a) and the fast (b) modulation. Phys. Rev. A 82, (2010) 022111 The time evolution of concurrence for the Gauss-Markov process for the slow (a) and the fast (b) modulation. Phys. Rev. A 82, (2010) 022111 The time evolution of the coherence (a) and the concurrence (b) for the two-state-jump Markov process. Phys. Rev. A 82, (2010) 022111 4. Concluding remarks We have systematically developed a theory of stochastic Liouville equation and the phenomenological feature of the theory is examined on the basis of the microscopic ground. The coherence and the entanglement of the quantum system are induced by the initial correlation between the relevant system and the environment. In the presence of the initial correlation, the process becomes nonstationary and is essential for the creation of the coherence and the entanglement. Appendix : Perturbative expansion for master equation The projection operator References 1) R.Kubo, J. Math. Phys. 4 (1962) 174. 2) R. Kubo, Adv. Chem. Phys. 15 (1969) 101. 3) Y. Tanimura, J. Phys. Soc. Jpn 75 (2006) 082001 and references therein. Initial correlation by TCL equation : 4) H.-P. Breuer, B. Kappler and F. Petryccione, Ann. of Phys. 291 (2001) 36. Initial correlation by other view point : 5) P. Stelmachovic and V. Buzek, Phys. Rev. A 64 (2001) 062106. 6) N. Boulant, J. Emerson, T. F. Havel and D. G. Cory, J. Chem. Phys. 121 (2004) 2955. 7) T. F. Jordan, A. Shaji and E. C. G. Sudarshan, Phys. Rev. A 70 (2004) 052110. Quantum mechanical two-state-jump model : 8) T. Arimitsu, M. Ban and F. S., Physica A 123 (1984) 131. 9) M. Ban, S. Kitajima, K. Maruyama and F.S., Phys. Lett. A 372 (2008) 351. Quantum mechanical Gaussian model : 10) Y. Hamano and F. S., J. Phys. Soc. Jpn., 51 (1982) 1727.