Download Chapter 29

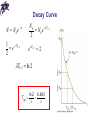
Chapter 29
Nuclear Physics
Properties of Nuclei
• All nuclei are composed of protons and neutrons
(exception: ordinary hydrogen)
• The atomic number, Z, equals the number of protons in
the nucleus
• The neutron number, N, is the number of neutrons in the
nucleus
• The mass number (not the same as the mass), A, is the
number of nucleons in the nucleus: A = Z + N
• Nucleon is a generic term used to refer to either a
proton or a neutron
• Symbol:
A
Z
Properties of Nuclei
X
• X is the chemical symbol of the element
• Example:
27
13
Al
• Mass number is 27; atomic number is 13; contains 13
protons and 14 = 27 – 13 neutrons
• The Z may be omitted since the element can be used to
determine Z
• The nuclei of all atoms of a particular element must
contain the same number of protons
Properties of Nuclei
• The nuclei may contain varying numbers of neutrons
• Isotopes of an element have the same Z but differing N
and A values. For example:
11
6
C
12
6
C
13
6
C
14
6
C
• The proton has a single positive charge, +e (e = 1.602
177 33 x 10-19 C)
• The electron has a single negative charge, -e
• The neutron has no charge, which makes it difficult to
detect
Mass
• It is convenient to express masses using unified mass
units, u, based on definition that the mass of one atom
of C-12 is exactly 12 u:
1 u = 1.660 559 x 10-27 kg
• Mass can also be expressed in MeV/c2 (from E = m c2)
1 u = 931.494 MeV/c2
Masses
Particle
kg
u
MeV/c2
1.6726 x 10-27
1.007276
938.28
Neutron 1.6750 x 10-27
1.008665
939.57
Electron 9.109 x 10-31
5.486x10-4
0.511
Proton
The Size of the Nucleus
• From scattering experiments, Rutherford found an
expression for how close an alpha particle moving
toward the nucleus can come before being turned
around by the Coulomb force
• The KE of the particle must be completely converted to
PE
2
2
mv
q1q2
(2e)( Ze)
 ke
 ke
2
r
d
• d gives an upper limit for the size
of the nucleus (e.g., for gold,
d = 3.2 x 10-14 m and for silver,
d = 2 x 10-14 m)
4ke Ze
d
mv2
The Size of the Nucleus
• Such small lengths are often expressed in femtometers
where 1 fm = 10-15 m Also called a fermi
• Since the time of Rutherford, many other experiments
have concluded that most nuclei are approximately
spherical with the average radius of
1
3
r  ro A
• ro = 1.2 x 10-15 m
Enrico Fermi
1901 – 1954
Density of Nuclei
• The volume of the nucleus (assumed to be spherical)
is directly proportional to the total number of
nucleons
• This suggests that all nuclei have nearly the same
density
• Nucleons combine to form a nucleus as though they
were tightly packed spheres
Nuclear Stability
• There are very large repulsive electrostatic forces
between protons
• These forces should cause the nucleus to fly apart
• The nuclei are stable because of the presence of
another, short-range force, called the nuclear force
• This is an attractive force that acts between all
nuclear particles
• The nuclear attractive force is stronger than the
Coulomb repulsive force at the short ranges within
the nucleus
Nuclear Stability
• Light nuclei are most stable if
N=Z
• Heavy nuclei are most stable
when N > Z
• As the number of protons
increase, the Coulomb force
increases and so more
nucleons are needed to keep
the nucleus stable
• No nuclei are stable when Z >
83
Chapter 29
Problem 7
(a) Find the speed an alpha particle requires to come
within 3.2 × 10−14 m of a gold nucleus. (b) Find the energy
of the alpha particle in MeV.
Binding Energy
• The total energy of the bound system (the nucleus) is
less than the combined energy of the separated
nucleons
• This difference in energy is called the binding energy of
the nucleus
• It can be thought of as the amount of energy you need
to add to the nucleus to break it apart into separated
protons and neutrons
Binding Energy
Binding Energy
• Except for light nuclei, the binding energy is about 8
MeV per nucleon
• The curve peaks in the vicinity of A = 60
• Nuclei with mass numbers greater than or less than 60
are not as strongly bound as those near the middle of
the periodic table
• The curve is slowly varying at A > 40, suggesting that
the nuclear force saturates
• A particular nucleon can interact with only a limited
number of other nucleons
Radioactivity
• Radioactivity is the spontaneous emission of radiation
• Radioactivity is the result of the decay (disintegration)
of unstable nuclei
• Three types of radiation can be emitted
• 1) Alpha particles: 4He nuclei)
• 2) Beta particles: either electrons or positrons (a
positron is the antiparticle of the electron, similar to the
electron except its charge is +e)
• 3) Gamma rays: high energy photons
Distinguishing Types of Radiation
• A radioactive beam is directed
into a region with a magnetic
field
• The gamma particles carry no
charge and they are not
deflected
• The alpha particles are deflected
upward
• The beta particles (electrons)
are deflected downward,
whereas the positrons would be
deflected upward
Penetrating Ability of Particles
• Alpha particles: barely penetrate a piece of paper
• Beta particles: can penetrate a few mm of aluminum
• Gamma rays: can penetrate several cm of lead
The Decay Constant
• The number of particles that decay in a given time is
proportional to the total number of particles in a
radioactive sample
ΔN = - λ N Δt
• λ: the decay constant; determines the rate at which the
material will decay
• The decay rate or activity, R, of a sample is defined as
the number of decays per second
N
R
 N
t
Decay Curve
• The decay curve follows the
equation
N = No e- λt
• Another useful parameter is the
half-life defined as the time it takes
for half of any given number of
radioactive nuclei to decay
T1 2 
ln 2


0.693

Decay Curve
N  N 0e
 t
1
 e T1 / 2
2
N0
 N 0 e T1 / 2
2
e T1 / 2  2
T1/ 2  ln 2
T1 2 
ln 2


0.693

Units
• The unit of activity, R, is the Curie, Ci: 1 Ci = 3.7 x 1010
decays/second
• The most commonly used units of activity are the mCi
and the µCi
• The SI unit of activity is the Becquerel, Bq: 1 Bq = 1
decay/second (therefore, 1 Ci = 3.7 x 1010 Bq)
Maria Skłodowska-Curie
1867 – 1934
Antoine Henri Becquerel
1852 – 1908
Chapter 29
Problem 24
A building has become accidentally contaminated with
radioactivity. The longest-lived material in the building is
strontium-90. (The atomic mass of is 89.907 7.) If the
building initially contained 5.0 kg of this substance, and
the safe level is less than 10.0 counts/min, how long will
the building be unsafe?
Decay – General Rules
• When one element changes into another element, the
process is called spontaneous decay or transmutation
• The sum of the mass numbers, A, must be the same on
both sides of the equation
• The sum of the atomic numbers, Z, must be the same
on both sides of the equation
• Conservation of mass-energy and conservation of
momentum must hold
Alpha Decay
• When a nucleus emits an alpha particle it loses two
protons and two neutrons (N decreases by 2; Z
decreases by 2; A decreases by 4)
• Symbolically
A
Z
X  ZA42Y  24He
• X: parent nucleus; Y: daughter nucleus
• Example: decay of 226 Ra (half life is
1600 years) 226
222
4
88
Ra  86 Rn  2 He
• Excess mass is converted into
kinetic energy
• Momentum of the two particles is equal and opposite
Beta Decay
• During beta decay, the daughter nucleus has the same
number of nucleons as the parent, but the atomic
number is changed by one
A
A

• Symbolically:
Z
X Z 1Y  e
A
Z
X Y e
A
Z 1

• The emission of the electron is from the nucleus, which
contains protons and neutrons
• The process occurs when a neutron is transformed into
a proton and an electron
• The energy must be conserved: the energy released in
the decay process should almost all go to kinetic
energy of the electron (KEmax)
Beta Decay
• Experiments showed that few electrons had this amount
of kinetic energy
• To account for this “missing” energy, Pauli proposed
the existence of another particle, which Fermi later
named the neutrino
• Properties of the neutrino:
• Zero electrical charge
• Mass much smaller than the
electron, probably not zero
• Spin of ½
• Very weak interaction with
matter
Beta Decay
• Symbolically
A
Z
X Z A1Y  e  
A
Z
X Z A1Y  e  
•  is the symbol for the neutrino;
antineutrino
is the symbol for the
• Therefore, in beta decay, the following pairs of particles
are emitted: either an electron and an antineutrino or a
positron and a neutrino
Gamma Decay
• Gamma rays are given off when an excited nucleus
“falls” to a lower energy state (similar to the process of
electron “jumps” to lower energy states and giving off
photons)
• The gamma ray photons are very high in energy relative
to light
• The excited nuclear states result from “jumps” made by
a proton or neutron
• The excited nuclear states may be the result of violent
collision or more likely of an alpha or beta emission
Gamma Decay
• Example of a decay sequence
12
5
B C *  e 
12
6

C*126C  
12
6
• The first decay is a beta emission
• The second step is a gamma emission
• The C* indicates the Carbon nucleus is in an excited
state
• Gamma emission doesn’t change either A or Z
Natural Radioactivity
• There are unstable nuclei found in nature, which give
rise to natural radioactivity
• Nuclei produced in the laboratory through nuclear
reactions exhibit artificial radioactivity
• Three series of natural radioactivity
exist (see table 29.2):
1) Uranium
2) Actinium
3) Thorium (processes through a
series of alpha and beta decays and
ends with a stable isotope of
lead, 208Pb)
Nuclear Reactions
• Structure of nuclei can be changed by bombarding
them with energetic particles
• These changes are called nuclear reactions
• As with nuclear decays, the atomic numbers and mass
numbers must balance on both sides of the equation
• E.g., alpha particle colliding with nitrogen:
4
2
He 
14
7
N  X  11H
X 
17
8
X 
17
8
O
• Balancing the equation allows for the identification of X,
so the reaction is
4
2
He 
14
7
N
17
8
O  11H
Chapter 29
Problem 39
Identify the unknown particles X and X’ in the following
1
nuclear reactions: X + 42 He → 24
+
Mg
12
0n
235
92
U + 01 n →
90
38
Sr + X + 2 01 n
2 11 H → 21 H + X + X’
Answers to Even Numbered Problems
Chapter 28:
Problem 4
ρn/ρa = 8.6 × 1013
Answers to Even Numbered Problems
Chapter 28:
Problem 8
a) 1.9 × 10-15 m
b) 7.4 × 10-15 m
Answers to Even Numbered Problems
Chapter 28:
Problem 10
(a) 1.11 MeV/nucleon
(b) 7.07 MeV/nucleon
(c) 8.79 MeV/nucleon
(d) 7.57 MeV/nucleon
Answers to Even Numbered Problems
Chapter 28:
Problem 18
(a)8.06 d
(b) It is probably 13153I
Answers to Even Numbered Problems
Chapter 28:
Problem 20
2.29 g
Answers to Even Numbered Problems
Chapter 28:
Problem 38
4
4 He
He,
2
2
Answers to Even Numbered Problems
Chapter 28:
Problem 42
a) 105B
b) –2.79 MeV