* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Point mutation wikipedia , lookup
Koinophilia wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Epigenetics of human development wikipedia , lookup
Genomic imprinting wikipedia , lookup
Human genetic variation wikipedia , lookup
Genome evolution wikipedia , lookup
Artificial gene synthesis wikipedia , lookup
History of genetic engineering wikipedia , lookup
Hybrid (biology) wikipedia , lookup
Skewed X-inactivation wikipedia , lookup
Designer baby wikipedia , lookup
Y chromosome wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Neocentromere wikipedia , lookup
Genetic drift wikipedia , lookup
X-inactivation wikipedia , lookup
Group selection wikipedia , lookup
Genome (book) wikipedia , lookup
Population genetics wikipedia , lookup
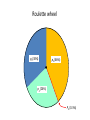
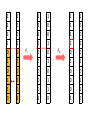
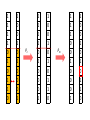
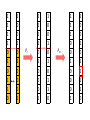
Genetic algorithms Optimization in DM f’(x) = 0 f’’(x) > 0 … minimum f’’(x) < 0 … maximum Optimization in DM • traditional methods (exact) – e.g. gradient based methods • heuristics (approximate) – deterministic – stochastic (chance) • e.g. genetic algorithms, simulated annealing, ant colony optimization, particle swarm optimization, memetic algorithms Optimization in DM • Applications of optimization techniques in DM are numerous. • Optimize parameters to obtain the best performance. • Optimize weights in NN • From many features, find the best (small) subset giving the best performance (feature selection). • … http://biology.unm.edu/ccouncil/Biology_124/Images/chromosome.gif Biology Inspiration • Every organism has a set of rules describing how that organism is built up from the tiny building blocks of life. These rules are encoded in genes. • Genes are connected together into long strings called chromosomes. • Genes + alleles = genotype. • Physical expression of the genotype = phenotype. locus • gene for color of teeth • allele for blue teeth • When two organisms mate they share their genes. The resultant offspring may end up having half the genes from one parent and half from the other. This process is called recombination (crossover). • Very occasionally a gene may be mutated. http://members.cox.net/amgough/Chromosome_recombination-01_05_04.jpg • Life on earth has evolved through the processes of natural selection, recombination and mutation. • The individuals with better traits will survive longer and produce more offsprings. – Their survivability is given by their fitness. • This continues to happen, with the individuals becoming more suited to their environment every generation. • It was this continuous improvement that inspired John Holland in 1970’s, to create genetic algorithms. GA step by step • Objective: find the maximum of the function O(x1, x2) = x12 + x22 – This function is called objective function. – And it will be use to evaluate the fitness. Adopted from Genetic Algorithms – A step by step tutorial, Max Moorkap, Barcelona, 29th November 2005 Encoding • A model parameters (x1, x2) are encoded into a binary strings. – Strings with 0 and 1. • How to encode (and decode back) real number as a binary string? – For each real valued variable x we need to know: • the domain of the variable x ϵ [xL,xU] • length of the gene k x1 ϵ [-1, 1] x2 ϵ [0, 3.1] 5-bit x1 x2 xL -1 0 xU 1 3.1 Stepsize 0.0645 0.1 𝑥𝑈 − 𝑥𝐿 stepsize = 𝑛 2 −1 number = 𝑥 𝐿 + stepsize × (decoded value of string) gene c1 = (0101110011) → (01011) = -1 + 11 * 0.0645 = -0.29 (10011) = 0 + 19 * 0.1 = 1.9 chromosome • At the start a population of N random models is generated • c1 = (0101110011) → (01011) = -1 + 11 * 0.0645 = -0.29 (10011) = 0 + 19 * 0.1 = 1.9 • c2 = (1111010110) → (11110) = -1 + 30 * 0.0645 = 0.935 (10110) = 0 + 22 * 0.1 = 2.2 • c3 = (1001010001) → (10010) = -1 + 18 * 0.0645 = 0.161 (10001) = 0 + 17 * 0.1 = 1.7 • c4 = (0110100001) → (01101) = -1 + 13 * 0.0645 = -0.161 (00001) = 0 + 1 * 0.1 = 0.1 • For each member of the population calculate the value of the objective function O(x1, x2) = x12 + x22 O1 = O(-0.29, 1.9) = 3.69 O2 = O(0.935, 2.2) = 5.71 O3 = O(0.161, 1.7) = 2.92 O4 = O(-0.161, 0.1) = 0.04 genotype phenotype • Chromosome with bigger fitness has higher probability to be selected for breeding. • We will use the following formula 𝑃𝑖 = 𝑂𝑖 𝑛 𝑗=1 𝑂𝑗 O1 = 3.69 O2 = 5.71 O3 = 2.92 O4 = 0.04 ∑Oj = 12.36 P1 = 0.30 P2 = 0.46 P3 = 0.24 P4 = 0.003 Roulette wheel p1(30%) p2 (46%) p3 (24%) P4 (0.3%) • Now select two chromosomes according to roulette wheel. – Allow the same chromosome to be selected more than once for breeding. • These two chromosomes will: 1. cross over 2. mutate • Let’s say c2 = (1111010110) and c3 = (1001010001) chromosomes were selected. • With probability Pc these two chromosomes will exchange their parts at the randomly selected locus (crossover point). 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 0 0 0 1 Pc 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 Pm 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 0 0 0 1 Pc 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 Pm 1 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1 1 1 1 0 1 0 1 1 0 1 0 0 1 0 1 0 0 0 1 Pc 1 1 1 1 0 1 0 0 0 1 1 0 0 1 0 1 0 1 1 0 Pm 1 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 • Crossover point is selected randomly. • Pc generally should be high, about 80%-95% – If the crossover is not performed, just clone two parents into new generation. • Pm should be very low, about 0.5%-1% – Perform mutation on each of the two offsprings at each locus. • Very big population size usually does not improve performance of GA. – Good size: 20-30, sometimes 50-100 reported as best – Depends on size of encoded string • Repeat the previous steps till the size of new population reaches N. – The new population replaces the old one. • Each cycle throught this algorithm is called generation. • Check whether termination criteria have been met. – Change in the mean fitness from generation to generation. – Preset the number of generations. 1. 2. 3. 4. 5. 6. [Start] Generate random population of N chromosomes (suitable solutions for the problem) [Fitness] Evaluate the fitness f(x) of each chromosome x in the population [New population] Create a new population by repeating following steps until the new population is complete 1. [Selection] Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected) 2. [Crossover] With a crossover probability cross over the parents to form a new offspring (children). If no crossover was performed, offspring is an exact copy of parents. 3. [Mutation] With a mutation probability mutate new offspring at each locus (position in chromosome). 4. [Accepting] Place new offspring in a new population [Replace] Use new generated population for a further run of algorithm [Test] If the end condition is satisfied, stop, and return the best solution in current population [Loop] Go to step 2. • Check the following applets – http://www.obitko.com/tutorials/geneticalgorithms/example-function-minimum.php – http://userweb.elec.gla.ac.uk/y/yunli/ga_demo/ maximum x = 6.092 y = 7.799 f(x,y)max = 100 More difficult problem O(x) = (x - 6)(x - 2)(x + 4)(x + 6) We search x ϵ [-10,20] 15-bit N = 20 6 generations O(-5.11) = -78.03 O(4.41) = -335.476 from Genetic Algorithms – A step by step tutorial, Max Moorkap, Barcelona, 29th November 2005 from Genetic Algorithms – A step by step tutorial, Max Moorkap, Barcelona, 29th November 2005 • The GA described so far is similar to Holland’s original GA. • It is now known as the simple genetic algorithm (SGA). • Other GAs use different: – Representations – Mutations – Crossovers – Selection mechanisms Selection enhancements • Balance fitness with diversity – fitness is favored over variability: a set of highly fit but suboptimal chromosomes will dominate the population, reducing the ability of the GA to find the global optimum – diversity is favored over fitness: model convergence will be too slow – e.g., one chromosome is extremely fit leading to high selection probability. It begins to reproduce and dominates the population (this is an example of selection pressure). • By reducing the diversity of the population, the ability of the GA to continue to explore new regions of the search space is impaired. • fitness-sharing function – decrease the fitness by the presence of similar population member – similar = small Hamming distance • do not allow matings between similar chromosomes • elitism – protect best chromosomes against destruction by crossover, mutation – retain certain number of chromosomes from one generation to another – greatly improves GA performance • rank selection – ranks the chromosomes according to fitness – avoids the selection pressure exerted by the proportional fitness method – but it also ignores the absolute differences among the chromosome fitnesses – Ranking does not take variability into account and provides a moderate adjusted fitness measure, since the probability of selection between chromosomes ranked k and k + 1 is the same regardless of the absolute differences in fitness. • tournament selection – Run several "tournaments" among a few (k) individuals chosen at random from the population. – For crossover, select best of these (the one with the best fitness). – Probability of selecting xi will depend on: • Rank of xi • Size of sample k – Higher k increases selection pressure • Whether contestants are picked with replacement – Picking without replacement increases selection pressure • Whether a fittest contestant always wins (deterministic) or this happens with probability p Crossover enhancements • Multipoint crossover • Uniform crossover Crossover OR mutation? • Decade long debate: which one is better • Answer (at least, rather wide agreement): – it depends on the problem, but – in general, it is good to have both – these two have different roles – a mutation-only-GA is possible, an xoveronly-GA would not work • Crossover is explorative – Discovering promising areas in the search space. – It makes a big jump to an area somewhere “in between” two (parent) areas. • Mutation is exploitative – Optimizing present information within an already discovered promising region. – Creating small random deviations and thereby not wandering far from the parents. • They complement each other. – Only crossover can bring together information from both parents. – Only mutation can introduce completely new information. Feature Selection, Feature Extraction Need for reduction • Classification of leukemia tumors from microarray gene expression data1 – 72 patients (data points) – 7130 features (expression levels of different genes) • Text mining, document classification – features are words • Quantitative Structure-Activity Relationship (QSAR) – features are molecular descriptors, there exist plenty of them 1 Xing, Jordan, Karp, Feature Selection for High-Dimensional Genomic Microarray Data, 2001 QSAR • biological activity – an expression describing the beneficial or adverse effects of a drug on living matter • Structure-Activity Relationship (SAR) – hypotheses that similar molecules have similar activities • molecular descriptor – mathematical procedure transforms chemical information encoded within a symbolic representation of a molecule into a useful number Molecular descriptor adjacency (connectivity) matrix total adj. index AV – sum all aij measure of the graph connectedness Randic connectivity indices measure of the molecular branching 2.183 QSAR • Form a mathematical/statistical relationship (model) between structural (physiochemical) properties and activity. • The mathematical expression can then be used to predict the biological response of other chemical structures. Selection vs. Extraction • In feature selection we try to find the best subset of the input feature set. • In feature extraction we create new features based on transformation or combination of the original feature set. • Both selection and extraction lead to the dimensionality reduction. • No clear cut evidence that one of them is superior to the other on all types of task. Why to do it? 1. We’re interested in features – we want to know which are relevant. If we fit a model, it should be interpretable. • • facilitate data visualization and data understanding reduce experimental costs (measurements) 2. We’re interested in prediction – features are not interesting in themselves, we just want to build a good predictor. • • faster training defy the curse of dimensionality