* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Trig form of Complex Numbers
Law of large numbers wikipedia , lookup
Infinitesimal wikipedia , lookup
Georg Cantor's first set theory article wikipedia , lookup
Location arithmetic wikipedia , lookup
Hyperreal number wikipedia , lookup
Large numbers wikipedia , lookup
Non-standard analysis wikipedia , lookup
History of trigonometry wikipedia , lookup
Real number wikipedia , lookup
Elementary mathematics wikipedia , lookup
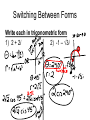
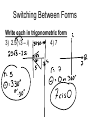
Trig form of Complex Numbers Objective: Be able to operate with complex numbers, and be able to convert complex numbers into Trig Form and vise versa. TS: Examining information from more than one view point. Warm-Up: Do the following operations: a)(3 + 5i) + (4 – 2i) b) (3 + 5i)(4 – 2i) Complex Numbers a+bi where i=√-1 (i2 = -1) Remember: They can be graphed on complex plane Imaginary axis 3 + 2i 1 Real axis 1 Absolute Value • Absolute value is the _________________ So |a + bi| = Imaginary Find |-3 + 4i| 1 |-2 – 6i| 1 Real Trig form of Complex Numbers To effectively work with powers and roots, it is helpful to use trig to express imaginary numbers. If θ is the angle formed to point (a, b) then Imaginary Thus a r θ b Real a = r cos θ & b = r sin θ + bi = (r cos θ) + (r sin θ) I = r cis θ where r = a a b 2 2 (r is called the modulus) and b tan a (θ is called the argument) Switching Between Forms Write each in trigonometric form 1) 2 + 2i 2) -1 – √3i Switching Between Forms Write each in trigonometric form 3) 2.5(√3 – i) 4) 7 Switching Between Forms Write each in trigonometric form 5) 1 + 2i Switching Between Forms Write each in standard form 1) 5(cos135° + i sin135°) 2) ¾ cis 330° Switching Between Forms Write each in standard form 3) 4) 1.5 cos i sin 2 2 5 4cis 6 You Try Represent 4 – 4√3i graphically, and find the trigonometric form of a number. Also find the absolute value of it. Click here for answers 5 Trig form 8cis 3 Imaginary 4 4 3i 8 Real 4 – 4√3i Click here for Question