* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download CH 9
Old quantum theory wikipedia , lookup
Specific impulse wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Classical mechanics wikipedia , lookup
Coriolis force wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Routhian mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Fictitious force wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Photon polarization wikipedia , lookup
Accretion disk wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Angular momentum operator wikipedia , lookup
Mass versus weight wikipedia , lookup
Seismometer wikipedia , lookup
Jerk (physics) wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Angular momentum wikipedia , lookup
Center of mass wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Moment of inertia wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Work (physics) wikipedia , lookup
Classical central-force problem wikipedia , lookup
Equations of motion wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
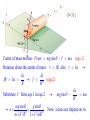
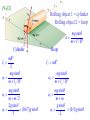
Chapter 9 Rotations of Rigid Bodies Up to this point when studying the motion of objects we have made the (implicit) assumption that these are “point objects” i.e. all the mass is concentrated at one point. In chapter 9 we will drop this assumption and study the rotation of rigid bodies. These are objects that do not change volume or shape. All that is needed to describe the rotations of rigid bodies is Newton’s laws of motion. From these we will develop the equations that describe rotational motion The following new concepts will be introduced: Moment of Inertia ( I ) Torque ( ) Angular Momentum ( L ) (9-1) Cartesian coordinates: (x, y) y Polar coordinates: (r, ) How to convert Cartesian to polar coordinates and vice versa P r y x O x (x, y) A (r, ) From triangle OAP we have: x r cos , y r sin r x y 2 2 , y tan x (9-2) (9-3) O Consider the rotation of a flat rigid body (the hand of a clock in the picture) in the xy-plane about the origin O which is fixed. Any point P of the rigid point (the tip of the hand in the picture) remains at a constant distance from O. All we need to describe the motion of P (and thus the motion of the rigid body) is the angle between the position vector r of point P and the x-axis. We express the angle as function of time (t) Note: Point O is the only point of the rotating body that does not move Rotation axis r In a three dimensional rigid body that rotates about a fixed axis all points on the rotation axis do not move Any point P on the rigid body rotates on a plane that is perpendicular to the rotation axis, on a circular orbit of fixed radius r (9-4) t + t t av (t t ) (t ) t d lim t dt t o t Consider a point P on a pot that is rotating on a potter’s wheel (fig.a). The position of P is described by the angle Average angular velocity Instantaneous angular velocity Units: rad/s (9-5) The angular velocity vector The vector is defined as follows: 1. Magnitude d dt 2. Direction and sense of Direction: The axis of coincides with the rotation axis Sense: Curl the fingers of the right hand in the direction of rotation. The thumb points along (9-6) Special case: Rotation with constant angular velocity d dt t 0 Integrate both sides from 0 to t t t d dt 0 d dt t 0 t - o t 0 o t This equation is the analog in rotational motion of the equation that describes motion along the x-axis with constant velocity: x(t) = xo + vt Note: In this chapter and the next we will take advantage of the similarity in form between equations that describe motion along a line and rotational motion. (9-7) (9-8) (t) = o + t eqs.1 Rotational motion with constant angular velocity Period T is the time required to complete one revolution ( = 2) Frequency f is the number of revolutions per second 1 f From the definition T Relationship between f and : In eqs. 1 we set o = 0 and = 2 2 = T = /f 2 f t + t In general the angular velocity is not t av (t t ) (t ) t constant but it changes with time. For this reason we introduce the notion of angular acceleration to describe the rate at which changes with t t d d 2 lim 2 t dt dt t 0 Average angular acceleration Units: rad/s2 Instantaneous angular acceleration (9-9) Motion with constant angular acceleration d dt t d dt t d dt 0 Integrate both sides from 0 to t 0 t 0 (9-10) t t o t 0 Compare with: v vo at o t d dt d dt Integrate both sides from 0 to t t t 0 d 0 dt o 0 dt 0 t dt 0 o t 0 2 0 2 2 t t o ot o ot 2 2 t t t t t at 2 Compare with: x xo vot 2 t 2 Non-uniform acceleration (9-11) In general angular acceleration is not constant r C In this most general case we decompose the vector a into two components: Rotation axis 1. ac (centripetal acceleration) that points towards the center C 2. at (tangential acceleration) that points along the tangent v2 dv d (r ) d 2 ac r , at r r r dt dt dt at r (9-12) Ri y vi Ri mi x O Rotational kinetic energy of a rigid body that rotates about an axis with angular velocity . Divide the object into N elements with masses m1, m2, …, mN Each mass element mi moves on a circle of radius Ri with speed vi = Ri. The kinetic energy of mi is given by: mi vi2 mi 2 Ri2 Ki 2 2 (9-13) Ri The kinetic energy of mi is: mi 2 Ri2 K i 2 The total rotational kinetic energy K is the sum of all the kinetic energies K K1 K 2 ... K N K y vi Ri mi x O 2 2 2 2 m R m R ... m R 11 1 2 1 N 2 The sum in the brackets is known as the "moment of inertia" or "rotational inertia" (symbol I) of the object I 2 K 2 mv 2 K in linear motion 2 Moment of Inertia I (9-14) I m1 R12 m2 R22 ... mN RN2 Ri Recipe for the determination of I for a given object 1. Divide the object into N elements with masses m1, m2, …, mN 2. The contribution of each element Ii = miRi2 3. Sum all the terms I = I1 + I2 + …. + IN 4. Take the limit as N I R 2 dm (9-15) I R 2 dm The moment of inertia of an object depends on: a. The mass and shape of the object, and b. the position of the rotation axis A x x’ Moment of inertia of a rod of length L and mass M Linear mass density = M/L Divide the rod into elements of length dx and mass dm = dx Consider a rotation axis through the center of mass O dI x dm x dx I CM 2 I CM 2 L/2 x x dx 3 L / 2 L / 2 L/2 3 2 L3 ( L) L2 ML2 12 12 12 L For a rotation axis through the end point A we have: I x 2 dx 0 L x L3 ( L) L2 ML2 I 3 3 3 3 0 3 (9-16) Parallel axis theorem I = ICM + md2 d is the distance between the rotation axis and the parallel axis that passes through the center of mass Moment of inertia I about any axis of an object of mass m = Moment of Inertia ICM about a parallel axis that passes through the center of mass + md2 (9-17) Torque of a force acting on a point P r F r O (9-18) Associated with any force F we can define a new vector , known as “the torque of F” , which plays an important role in rotational dynamics Magnitude of = Fr r = “arm of the moment” r = rsin = Frsin Direction of If the force tends to rotate the object on which it acts the clockwise (CW) direction (as in the picture) the torque points into the plane of rotation and has a negative sign. If on the other hand the rotation is counterclockwise (CCW) the torque points out of the plane and is positive (9-19) The equivalent of the “second law” in rotational dynamics Consider the object shown in the figure which can rotate about a vertical axis. We divide the object into element of masses m1, m2, … mN On each of these elements we apply a force F1, F2, ... FN For simplicity we assume that these forces are perpendicular to the object. Consider one element of mass mi The force Fi results in a torque i = Firi , Fi = miai = miri i = miri2 Total torque = 1+ 2 + …+ N = (m1r12 +…+ mNrN2) = I Thus: I Compare this with: F = ma Example (9-6) page 250. A bucket of mass m = 12 kg is connected via a rope to a cylindrical flywheel of mass M = 88 kg and radius R = 0.5 m. The bucket is dropped and the flywheel is allowed to spin. Determine the angular velocity of the flywheel after the bucket has fallen for 5 s. (9-20) System bucket R a Fynet T mg ma T mg ma (eqs.1) System bucket TR (eqs.2) We substiture T from eqs.1 into eqs.2 (mg ma ) R (eqs.3) a MR 2 a MRa I I (eqs.4) R 2 R 2 Compare eqs.3 and eqs.4 MRa (mg - ma) R 2 m 12 ag 9.8 2.1 m/s 2 M 12 88 / 2 m 2 (9-21) R a The acceleration of the bucket is also the acceleration of the rope and therefore the tangential acceleration at the rim of the flywheel a 2.1 m/s 2 a 2.1 4.2 rad/s 2 R 0.5 o t 4.2 5 21 rad/s (9-22) Torque of the gravitational force R The torque of the gravitational force on a rigid body Fg is equal to the torque of Fg acting at the center of mass of the object Thus = mgR R = Rsin = mgRsin (9-23) Analogies between linear and rotational motion Linear Motion Rotational Motion x (distance) (rotation angle) v (velocity) (angular velocity) a (acceleration) (angular acceleration) m (mass) I (moment of inertia) F (force) (torque) p = (linear momentum) p = mv L (angular momentum) L=I (9-24) Angular momentum L L By analogy to the definition of the linear momentum p mv we define the vector of angular momentum L as follows: L I units: kg.m2/s Since I > 0 L is parallel to d L d (I ) d I I dt dt dt dp F for linear motion dt dL dt (9-25) Conservation of angular momentum L dL dt dL If 0 0 dt L is a constant vector If the torque of all external forces on a rigid body is zero then the angular momentum L does not change (it is conserved L 0 (9-26) Rolling When a wheel rolls on flat ground it executes two types of motion a. All points on the rim rotate about the center of mass with angular velocity b. The center of mass and all other points on the wheel move with velocity vcm Note 1: The total velocity of any point on the wheel is the vector some of the velocities due to these two motions Note 2: and vcm are connected (9-27) Rolling vcm vcm L1 L1 is the distance traveled in one revolution of the wheel Thus: L1 vcmT L1 is given by the equation: L1 =2 R = circumference of the rim of the wheel vcmT 2 R vcm vcm R 2 R R T (9-28) Kinetic energy of a rolling object vcm vcm P I P 2 K I P is the wheel's moment of inertia about point P 2 I P I cm mR 2 (parallel axis theorem) 2 2 2 2 I I mv m( R ) 2 cm K ( I cm mR ) cm cm 2 2 2 2 2 The first term in the expression for K is the rotational energy about the center of mass. The second term is the kinetic energy 2 due to the translation of the center of mass. (9-29) Find the acceleration of the center of mass of the rolling object (moment of inertia about the center of mass Icm , mass m, radius R) as it rolls down an inclined plane of angle mg sin a m I / R2 (9-30) (9-31) Center of mass motion: Fxnet mg sin - f ma (eqs.1) Rotation about the center of mass: fR also I Ia Ia fR I f 2 R R Substitute f from eqs.1 in eqs.2 mg sin g sin a 2 mI /R 1 I / mR 2 (eqs.2) Ia mg sin R2 ma Note: a does not depend on m (9-32) Rolling object 1 = cylinder Rolling object 2 = hoop mg sin a m I / R2 Cylinder mR 2 I1 2 mg sin a1 m I1 / R 2 mg sin a1 m m/2 2 g sin a1 (0.67) g sin 3 Hoop I 2 mR 2 mg sin a2 m I2 / R2 mg sin a2 mm g sin a2 (0.5) g sin 2