* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Momentum
Coriolis force wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
Center of mass wikipedia , lookup
Monte Carlo methods for electron transport wikipedia , lookup
Routhian mechanics wikipedia , lookup
Fictitious force wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Old quantum theory wikipedia , lookup
Renormalization group wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Tensor operator wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Uncertainty principle wikipedia , lookup
Mass versus weight wikipedia , lookup
Rigid body dynamics wikipedia , lookup
Matter wave wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Quantum vacuum thruster wikipedia , lookup
Specific impulse wikipedia , lookup
Classical mechanics wikipedia , lookup
Accretion disk wikipedia , lookup
Photon polarization wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Centripetal force wikipedia , lookup
Work (physics) wikipedia , lookup
Equations of motion wikipedia , lookup
Angular momentum wikipedia , lookup
Angular momentum operator wikipedia , lookup
Classical central-force problem wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Momentum
Chapter 9
Impulse and Momentum
Momentum
p= mv
Impulse Momentum Change Theorem
The sports announcer says "Going into the allstar break, the Chicago White Sox have the
momentum." The headlines declare "Chicago
Bulls Gaining Momentum." The coach pumps up
his team at half-time, saying "You have the
momentum; the critical need is that you use that
momentum and bury them in this third quarter."
Sports vs. Physics
Momentum is a commonly used term in sports. A
team that has the momentum is on the move
and is going to take some effort to stop. A team
that has a lot of momentum is really on the move
and is going to be hard to stop. Momentum is a
physics term; it refers to the quantity of motion
that an object has. A sports team which is "on
the move" has the momentum. If an object is in
motion ("on the move") then it has momentum.
Defining Momentum
Momentum can be defined as "mass in motion." All
objects have mass; so if an object is moving, then it
has momentum - it has its mass in motion. The
amount of momentum which an object has is
dependent upon two variables: how much stuff is
moving and how fast the stuff is moving.
Momentum depends upon the variables mass and
velocity. In terms of an equation, the momentum of
an object is equal to the mass of the object times
the velocity of the object.
The Equations
Momentum = mass * velocity In physics, the
symbol for the quantity momentum is the small
case "p"; thus, the above equation can be
rewritten as
p = m * v
where m = mass and v=velocity. The equation
illustrates that momentum is directly proportional
to an object's mass and directly proportional to
the object's velocity
Defining the Units of Measure
The units for momentum would be mass units times
velocity units. The standard metric unit of momentum is
the kg*m/s. While the kg*m/s is the standard metric unit
of momentum, there are a variety of other units which
are acceptable (though not conventional) units of
momentum; examples include kg*mi/hr, kg*km/hr, and
g*cm/s. In each of these examples, a mass unit is
multiplied by a velocity unit to provide a momentum unit.
This is consistent with the equation for momentum.
Vector or Scalar?
Momentum is a vector quantity. As discussed in an
earlier unit, a vector quantity is a quantity which is fully
described by both magnitude and direction. To fully
describe the momentum of a 5-kg bowling ball moving
westward at 2 m/s, you must include information about
both the magnitude and the direction of the bowling ball.
It is not enough to say that the ball has 10 kg*m/s of
momentum; the momentum of the ball is not fully
described until information about its direction is given.
Defining Direction
The direction of the momentum vector is the
same as the direction of the velocity of the ball.
In a previous unit, it was said that the direction of
the velocity vector is the same as the direction
which an object is moving. If the bowling ball is
moving westward, then its momentum can be
fully described by saying that it is 10 kg*m/s,
westward. As a vector quantity, the momentum
of an object is fully described by both magnitude
and direction.
Which variable (mass or velocity) defines momentum?
From the definition of momentum, it becomes
obvious that an object has a large momentum if
either its mass or its velocity is large. Both variables
are of equal importance in determining the
momentum of an object. Consider a Mack truck and
a roller skate moving down the street at the same
speed. The considerably greater mass of the Mack
truck gives it a considerably greater momentum. Yet
if the Mack truck were at rest, then the momentum
of the least massive roller skate would be the
greatest; for the momentum of any object which is
at rest is 0. Objects at rest do not have momentum they do not have any "mass in motion." Both
variables - mass and velocity - are important in
comparing the momentum of two objects.
Conceptualizing Momentum
The momentum equation can help us to think about how
a change in one of the two variables might effect the
momentum of an object. Consider a 0.5-kg physics cart
loaded with one 0.5-kg brick and moving with a speed of
2.0 m/s. The total mass of loaded cart is 1.0 kg and its
momentum is 2.0 kg*m/s. If the cart was instead loaded
with three 0.5-kg bricks, then the total mass of the
loaded cart would be 2.0 kg and its momentum would be
4.0 kg*m/s. A doubling of the mass results in a doubling
of the momentum.
Problem Solving Momentum
Similarly, if the 2.0-kg cart had a velocity of 8.0
m/s (instead of 2.0 m/s), then the cart would
have a momentum of 16.0 kg*m/s (instead of 4.0
kg*m/s). A quadrupling in velocity results in a
quadrupling of the momentum. These two
examples illustrate how the equation p=m*v
serves as a "guide to thinking" and not merely a
"recipe for algebraic problem-solving."
1. Determine the momentum of a ...
60-kg halfback moving eastward at 9 m/s.
1000-kg car moving northward at 20 m/s.
40-kg freshman moving southward at 2 m/s.
1 Answers
A) p = m * v
(60 kg)(9m/s) =
540 kg * m /s
B) p = m * v
(1000 kg)(20 m/s)
20,000 kg* m/s
C) p = m * v
40 kg * 2 m/s
80 kg * m/s
2. A car possesses 20 000 units of momentum. What would be the
car's new momentum if ...
its velocity were doubled.
its velocity were tripled.
its mass were doubled (by adding more passengers
and a greater load)
both its velocity were doubled and its mass were
doubled.
2 answers
A) 40, 000 units (doubling the velocity will double
the momentum)
B) 60, 000 units (tripling the velocity will triple the
momentum
C) 40, 000 units (doubling the mass will double
the momentum)
D) 80, 000 units (doubling the mass and doubling
the velocity will quadruple the momentum)
3. A halfback (m = 60 kg), a tight end (m = 90 kg), and a
lineman (m = 120 kg) are running down the football field. Consider
their ticker tape patterns below.
Compare the velocities of these three
players. How many times greater is the
velocity of the halfback and the velocity of the
tight end than the velocity of the lineman?
Connecting Momentum and Impulse
As mentioned in the previous part of this lesson,
momentum is a commonly used term in sports.
When a sports announcer says that a team has the
momentum they mean that the team is really on the
move and is going to be hard to stop. An object with
momentum is going to be hard to stop. To stop such
an object, it is necessary to apply a force against its
motion for a given period of time. The more
momentum which an object has, the harder that it is
to stop. Thus, it would require a greater amount of
force or a longer amount of time (or both) to bring an
object with more momentum to a halt. As the force
acts upon the object for a given amount of time, the
object's velocity is changed; and hence, the object's
momentum is changed.
Momentum in sports
The concepts in the above paragraph should not seem
like abstract information to you. You have observed this
a number of times if you have watched the sport of
football. In football, the defensive players apply a force
for a given amount of time to stop the momentum of the
offensive player who has the ball. You have also
experienced this a multitude of times while driving. As
you bring your car to a halt when approaching a stop
sign or stoplight, the brakes serve to apply a force to the
car for a given amount of time to stop the car's
momentum. An object with momentum can be stopped if
a force is applied against it for a given amount of time.
Picture Illustration
Revisiting Force Balance
A force acting for a given amount of time will change an
object's momentum. Put another way, an unbalanced
force always accelerates an object - either speeding it up
or slowing it down. If the force acts opposite the object's
motion, it slows the object down. If a force acts in the
same direction as the object's motion, then the force
speeds the object up. Either way, a force will change the
velocity of an object. And if the velocity of the object is
changed, then the momentum of the object is changed.
Back to Newton’s Second Law
These concepts are merely an outgrowth of
Newton's second law as discussed in an earlier
unit. Newton's second law (Fnet=m*a) stated that
the acceleration of an object is directly
proportional to the net force acting upon the
object and inversely proportional to the mass of
the object. When combined with the definition of
acceleration (a=change in velocity/time), the
following equalities result.
Formulas of Newton’s 2nd Law
Multiply both sides by t
Examining the Equation
This equation is one of two primary equations to
be used in this unit. To truly understand the
equation, it is important to understand its
meaning in words. In words, it could be said that
the force times the time equals the mass times
the change in velocity. In physics, the quantity
Force*time is known as the impulse. And since
the quantity m*v is the momentum, the quantity
m*"Delta "v must be the change in momentum.
The equation really says that the Impulse =
Change in momentum
Collisions
One focus of this unit is to understand the
physics of collisions. The physics of collisions
are governed by the laws of momentum; and the
first law which we discuss in this unit is
expressed in the above equation. The equation
is known as the impulse-momentum change
equation. The law can be expressed this way:
Expressions of collisions
In a collision, an object experiences a force for a specific
amount of time which results in a change in momentum
(the object's mass either speeds up or slows down). The
impulse experienced by the object equals the change in
momentum of the object. In equation form, F * t = m *
Delta v.
Objects in collisions with impulse
In a collision, objects experience an impulse;
the impulse causes (and is equal to) the
change in momentum. Consider a football
halfback running down the football field and
encountering a collision with a defensive
back. The collision would change the
halfback's speed (and thus his momentum).
If the motion was represented by a ticker
tape diagram, it might appear as follows:
Putting numbers in…
At approximately the tenth dot on the diagram, the
collision occurs and lasts for a certain amount of
time; in terms of dots, the collision lasts for
approximately nine dots. In the halfback-defensive
back collision, the halfback experiences a force
which lasts for a certain amount of time to change
his momentum. Since the collision causes the
rightward-moving halfback to slow down, the force
on the halfback must have been directed leftward. If
the halfback experienced a force of 800 N for 0.9
seconds, then we could say that the impulse was
720 N*s. This impulse would cause a momentum
change of 720 kg*m/s. In a collision, the impulse
experienced by an object is always equal to the
momentum change.
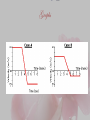
Tennis Ball Collision
Now consider a collision of a tennis ball with a wall.
Depending on the physical properties of the wall (its
elastic nature), the speed at which the ball rebounds
from the wall upon colliding with it will vary. The
diagrams below depict the changes in velocity of the
same ball. For each representation (vector diagram, v-t
graph, and ticker tape pattern), indicate which case (A or
B) has the greatest change in velocity, greatest
acceleration, greatest momentum change, and greatest
impulse. Support each answer.
Vector Diagrams
Tabulate your Answers
Greatest velocity change?
Greatest acceleration?
Greatest momentum
change?
Greatest Impulse?
Answers
Greatest velocity change? B (changes from +30 m/s to
-28 m/s which is a change of 58 m/s and A only
changes -15 m/s)
Greatest acceleration? B, because it has the greatest
velocity change and acceleration is dependent on
velocity change.
Greatest momentum change? B, because momentum
is dependent on velocity and the change in velocity is
greatest in B.
Greatest Impulse? B, impulse is momentum change
and the momentum change is greatest in B.
Graphs
Setting up your answers
Greatest velocity
change?
Greatest acceleration?
Greatest momentum
change?
Greatest Impulse?
Answers
Greatest
velocity
change?
Greatest in A because it changes from
+5 m/s to -3 m/s which is a change of 8
whereas B only changes 4 m/s
Greatest
A, acceleration is greatest because
acceleration? velocity change is greatest in A
Greatest
momentum
change?
A, momentum is dependent on velocity
change and that is greatest in A
Greatest
Impulse?
A, Impulse equals the change in
momentum
Using Ticker Tape Diagrams
Organizing the Answers
Greatest velocity
change?
Greatest acceleration?
Greatest momentum
change?
Greatest Impulse?
Answers
Greatest
velocity
change?
B, vi is the same for both, but object
B rebounds with a greater speed so it
goes from -10 to +5 m/s whereas A
goes from -10 m/s to +2 m/s.
Greatest
acceleration?
B, acceleration is dependent on
velocity change
Greatest
momentum
change?
B, Momentum is dependent on
velocity
Greatest
Impulse?
B, impulse is defined as the change
in momentum
Recapping the Examples
Observe that each of the collisions above
involved the rebound of a ball off a wall. Observe
that the greater the rebound effect, the greater
the acceleration, momentum change, and
impulse. A rebound is a special type of collision
involving a direction change; the result of the
direction change is large velocity change.
Elastic Collisions
On occasions in a rebound collision, an object
will maintain the same or nearly the same speed
as it had before the collision. Collisions in which
objects rebound with the same speed (and thus,
the same momentum and kinetic energy) as they
had prior to the collision are known as elastic
collisions. In general, elastic collisions are
characterized by a large velocity change, a large
momentum change, a large impulse, and a large
force.
Momentum and collisions
Use the impulse-momentum change principle to
fill in the blanks in the following rows of the table.
As you do, keep these three major truths in
mind:
the impulse experienced by an object is the
force*time
the momentum change of an object is the
mass*velocity change
the impulse equals the momentum change
Create this Chart
Force
(N)
time
(s)
1.
0.010
2.
0.100
3.
0.010
4.
-20
000
5.
-200
Mom.
Impuls
Chg.
e
(kg*m
(N*s)
/s)
-40
Mass
(kg)
Vel.
Chg.
(m/s)
10
-4
10
-200
50
-200
1.0
-8
50
Answers
Force (N)
time
(s)
Mom.
Impuls
Chg.
Mass
e
(kg*m (kg)
(N*s)
/s)
1.
-4000 N
0.010
-40
-40
10
-4
2.
-400 N
0.100
-40
-40
10
-4
-200
-200
50
-4
4. -20 000
.010 s -200
-200
25
-8
5.
1.0
-200
50
-4
3. -20, 000 N 0.010
-200
-200
Vel.
Chg.
(m/s)
Reflections on the Table
There are a few observations which can be made in the
above table which relate to the computational nature of the
impulse-momentum change theorem. First, observe that the
answers in the table above reveal that the third and fourth
columns are always equal; that is, the impulse is always
equal to the momentum change. Observe also that the if
any two of the first three columns are known, then the
remaining column can be computed; this is true because
the impulse=force*time. Knowing two of these three
quantities allows us to compute the third quantity. And
finally, observe that knowing any two of the last three
columns allows us to compute the remaining column; this is
true since momentum change = mass*velocity change.
Additional Thoughts
There are also a few observations which can be made
which relate to the qualitative nature of the impulsemomentum theorem. An examination of rows 1 and 2 show
that force and time are inversely proportional; for the same
mass and velocity change, a tenfold increase in the time of
impact corresponds to a tenfold decrease in the force of
impact. An examination of rows 1 and 3 show that mass and
force are directly proportional; for the same time and
velocity change, a fivefold increase in the mass corresponds
to a fivefold increase in the force required to stop that mass.
Finally, an examination of rows 3 and 4 illustrate that mass
and velocity change are inversely proportional; for the same
force and time, a twofold decrease in the mass corresponds
to a twofold increase in the velocity change.
Examples
Express your understanding of the impulsemomentum change theorem by answering the
following questions.
Example 1
1. A 0.50-kg cart (#1) is pulled with a 1.0-N force for 1
second; another 0.50 kg cart (#2) is pulled with a 2.0 Nforce for 0.50 seconds. Which cart (#1 or #2) has the
greatest acceleration? Explain.
Answer 1
Cart 2 has the greatest acceleration. Recall that force is
dependent on acceleration and mass. Both carts have
the same mass but cart 2 has the greatest force.
Example 2
Which cart (#1 or #2) has the greatest impulse? Explain.
Answer 2
The impulse is the same for both carts. Impulse is force *
time which calculates each cart to 1 N * s for each.
Example 3
Which cart (#1 or #2) has the greatest change in
momentum? Explain.
Answer 3
The momentum change is the same for both carts.
Momentum change equals the impulse. If both carts
have the same impulse then they both have the same
momentum change.
Example 4
2. In a phun physics demo, two identical balloons (A
and B) are propelled across the room on horizontal
guide wires. The motion diagrams (depicting the
relative position of the balloons at time intervals of
0.05 seconds) for these two balloons are shown
below.
Question 4a
Which balloon (A or B) has the greatest acceleration?
Explain.
Answer 4a
Balloon B has the greatest acceleration The rate at
which the velocity changes is greatest for balloon B, this
is shown by the fact that the speed (distance/time)
changes most rapidly.
Example 4B
Which balloon (A or B) has the greatest final velocity?
Explain.
Answer 4B
Balloon B has the greatest final velocity. At the end of the
diagram, the distance traveled in the latest interval is
greatest for Balloon B.
Question 4C
Which balloon (A or B) has the greatest momentum
change? Explain.
Answer 4C
Balloon B has the greatest momentum change. The final
velocity is greatest for Balloon B, its velocity change is
also the greatest. Momentum change depends on
velocity change. The balloon with the greatest velocity
change will have the greatest momentum change.
Question 4D
Which balloon (A or B) experiences the greatest
impulse? Explain.
Answer 4D
The impulse is the same for each car. The impulse
equals the momentum change. If the momentum change
is the same for each car, then so must be the impulse.
Question 5
The diagram to the
right depicts the
before- and aftercollision speeds of a
car which undergoes
a head-on-collision
with a wall. In Case
A, the car bounces
off the wall. In Case
B, the car "sticks" to
the wall.
Question 5A
In which case (A or B) is the change in velocity the
greatest? Explain.
Answer 5A
Case A has the greatest velocity change. The velocity
change is -9 m/s in case A and only -5 m/s in case B.
Question 5B
In which case (A or B) is the change in momentum the
greatest? Explain.
Answer 5B
Case A has the greatest momentum change. The
momentum change is dependent on the velocity change;
the object with the greatest velocity change has the
greatest momentum change.
Question 5C
In which case (A or B) is the impulse the greatest?
Explain.
Answer 5C
The impulse is greatest for Car A. The impulse equals
the momentum change. If the momentum change is
greatest for car A then the impulse is greatest.
Question 5D
In which case (A or B) is the force which acts upon the
car the greatest (assume contact times are the same in
both cases)? Explain.
Answer 5D
The impulse is greatest for car A. The force is related to
impulse (I = F * t). The bigger impulse for car A is
attributed to the greatest force upon car A. Recall that
the rebound effect is characterized by larger forces; car
A is the car which rebounds.
Question 6
Rhonda, who has a mass of 60.0 kg, is riding at 25.0 m/s
in her sports car when she must suddenly slam on the
brakes to avoid hitting a dog crossing the road. She
strikes the air bag, which brings her body to a stop in
0.400 s. What average force does the seat belt exert on
her?
Answer 6
F = m x change in velocity)/time
F = (60 kg x 25 m/s)/ 0.400 s
F = 3750 N
Question 6B
If Rhonda had not been wearing her seat belt and not
had an air bag, then the windshield would have stopped
her head in 0.001 s. What average force would the
windshield have exerted on her?
Answer 6B
F = (m x D v ) / t
F = (60 kg x 25 m/s) / 0.001 s
F = 1,500,000 N
Question 7
A hockey player applies an average force of 80.0 N to a
0.25 kg hockey puck for a time of 0.10 seconds.
Determine the impulse experienced by the hockey puck.
Answer 7
Impulse = Force x time
I = 80 N x 0.1 s
I=8Nxs
Ex. 8
If a 5-kg object experiences a 10-N force for a duration
of 0.1 seconds, then what is the momentum change of
the object?
Question 8
Momentum change = 1.0 kg m/s
The momentum change = mass x velocity
change
But since velocity change is unknown, another
strategy must be used to find the momentum
change. The strategy involves first finding the
impulse (I = F x t). Since impulse = momentum
change, the answer is 1 N x s.
Angular Momentum
Angular Momentum
Defn. quantity of motion used with objects rotating about
a fixed axis
Changes when torque acts on the object
Product of mass x displacement from center x velocity
Ex. Orbiting planets have a constant angular momentum
and a torque of zero because gravitational force is
directly toward the sun
The Conservation of Momentum
Momentum and Isolated Systems
The previous part of Lesson 2 focused on the
Law of Conservation of Momentum. It was
stated that ...
For a collision occurring between object 1 and
object 2 in an isolated system, the total
momentum of the two objects before the
collision is equal to the total momentum of the
two objects after the collision. That is, the
momentum lost by object 1 is equal to the
momentum gained by object 2.
Total system momentum is conserved for collisions
occurring in isolated systems. But what makes a system
of objects an isolated system? And is momentum
conserved if the system is not isolated? This is the focus
of this lesson.
A system is a collection of two or more objects. An
isolated system is a system which is free from the
influence of a net external force. There are two criteria
for the presence of a net external force; it must be...
a force which originates from a source other than the two
objects of the system
a force that is not balanced by other forces
Consider the collision of two balls on the billiards
table. The collision occurs in an isolated system
as long as friction is small enough that its
influence upon the momentum of the billiard
balls can be neglected. If so, then the only
unbalanced forces acting upon the two balls are
the contact forces which they apply to one
another. These two forces are considered
internal forces since they result from a source
within the system - that source being the contact
of the two balls. For such a collision, total
system momentum is conserved.
Read the following descriptions of a collision and
evaluate whether or not the collision occurs in an
isolated system. If it is not an isolated system, then
identify the net external force.
Collision
Description
1 Two cars collide on a
gravel roadway on
which frictional
forces are large.
2 Hans Full is doing
the annual
vacuuming. Hans is
pushing the Hoover
vacuum cleaner
across the living
room carpet.
3 Two air track gliders
collide on a frictionfree air track.
Isolated
System?
Yes or
No
If No, then the external
force is...
Collision
Description
1
2
3
Isolated
System?
Yes or
No
Two cars collide on
a gravel roadway
on which frictional
forces are large.
No
Hans Full is doing
the annual
vacuuming. Hans is
pushing the Hoover
vacuum cleaner
across the living
room carpet.
No
Two air track
gliders collide on a
friction-free air
track.
Yes
If No, then the external
force is...
The friction between
the cars and the road is
an external force
The friction between
the cleaner and the
floor and the applied
force by Hans are
external forces
There are no external
forces. The system is
isolate
If a system is not isolated, then the total system
momentum is not conserved. To understand this
concept, we will return to our original analogy.
Suppose Jack and Jill (each with $100 in their pockets)
undergo a financial interaction in which Jack hands Jill
$50 for the purchase of some goods. If Jack and Jill
were isolated from the influence of the rest of the world,
then Jack would end up with $50 and Jill would end up
with $150. The total money in the system would be $200
both before and after the transaction; total system
money would be conserved. If however, a third influence
enters from outside of the system to take away or (more
fortunately) to add money to the system, then total
system momentum would not be conserved. If a thief
interfered with his filthy hands so as to steal $20, then
perhaps Jack would finish with $40 and Jill would finish
with $140. In the case of a non-isolated system, the total
momentum is not conserved.
Using Equations as a "Recipe" for
Algebraic Problem-Solving
As discussed in a previous part of Lesson 2,
total system momentum is conserved for
collisions between objects in an isolated system.
The momentum lost by one object is equal to the
momentum gained by another object. For
collisions occurring in an isolated systems, there
are no exceptions to this law. This law becomes
a powerful law in physics because it allows for
predictions of the before- and after-collision
velocities (or mass) of an object. In this portion
of Lesson 2, the law of momentum conservation
will be used to make such predictions. The law
of momentum conservation will be combined
with the use of a "momentum table" and some
algebra skills to solve problems involving
collisions occurring in isolated systems.
Concept Example
A 15-kg medicine ball is thrown at a velocity of 20 km/hr
to a 60-kg person who is at rest on ice. The person
catches the ball and subsequently slides with the ball
across the ice. Determine the velocity of the person and
the ball after the collision.
Beginning to form a solution
Such a motion can be considered as a collision between
a person and a medicine ball. Before the collision, the
ball has momentum and the person does not. The
collision causes the ball to lose momentum and the
person to gain momentum. After the collision, the ball
and the person travel with the same velocity ("v") across
the ice. Draw a diagram!
If it can be assumed that the effect of friction between
the person and the ice is negligible, then the collision
has occurred in an isolated system. Momentum should
be conserved and the problem can be solved for v by
use of a momentum table as shown below.
Before Collision
After Collision
Person
0
60 * v
Medicine ball
300
15 * v
Total
300
300
Observe in the table above that the known information
about the mass and velocity of the two objects was used
to determine the before-collision momenta of the
individual objects and the total momentum of the system.
Since momentum is conserved, the total momentum
after the collision is equal to the total momentum before
the collision. Finally, the expression "60*v" and "15*v"
was used for the after-collision momentum of the person
and the medicine ball. To solve the problem for "v" (the
velocity of both the objects after the collision), set the
sum of the individual momentum of the two objects equal
to the total momentum. The following equation results:
Solution
60*v + 15*v = 300
75*v = 300
v = 4 km/hr
Using algebra skills, it can be shown that v=4
km/hr. Both the person and the medicine ball
move across the ice with a velocity of 4 km/hr
after the collision. (NOTE: The unit km/hr is the
unit on the answer since the original velocity as
stated in the question had units of km/hr.)
Granny (m=80 kg) whizzes around the rink with a
velocity of 6 m/s. She suddenly collides with Ambrose
(m=40 kg) who is at rest directly in her path. Rather than
knock him over, she picks him up and continues in
motion without "braking." Determine the velocity of
Granny and Ambrose. Assume that no external forces
act on the system so that it is an isolated system.
Before the collision, Granny has momentum and
Ambrose does not. The collision causes Granny to lose
momentum and Ambrose to gain momentum. After the
collision, the Granny and Ambrose move with the same
velocity ("v") across the rink.
Since the collision between Granny and Ambrose occurs
in an isolated system, total system momentum is
conserved. The total momentum before the collision
(possessed solely by Granny) equals the total
momentum after the collision (shared between Granny
and Ambrose). The table below depicts this principle of
momentum conservation.
Before Collision
After Collision
Granny
80 * 6 = 480
80 * v
Ambrose
0
40 * v
Total
480
480
Observe in the table above that the known information
about the mass and velocity of Granny and Ambrose
was used to determine the before-collision momenta of
the individual objects and the total momentum of the
system. Since momentum is conserved, the total
momentum after the collision is equal to the total
momentum before the collision. Finally, the expression
"80*v" and "40*v" was used for the after-collision
momentum of the Granny and Ambrose. To solve the
problem for "v" (the velocity of both persons after the
collision), set the sum of the individual momentum of the
two objects equal to the total momentum. The following
equation results:
80*v + 40*v = 480
120*v = 480
v = 4 m/s
Using algebra skills, it can be shown that v = 4
m/s. Both Granny and Ambrose move across the
ice with a velocity of 4 m/s after the collision.
(NOTE: The unit m/s is the unit on the answer
since the original velocity as stated in the
question had units of m/s.)
The two collisions above are examples of
inelastic collisions. Technically, an inelastic
collision is a collision in which the kinetic energy
of the system of objects is not conserved. In an
inelastic collision, the kinetic energy of the
colliding objects is transformed into other nonmechanical forms of energy such as heat energy
and sound energy. The subject of energy will be
treated in a later unit of The Physics Classroom.
To simplify matters, we will consider any
collisions in which the two colliding objects stick
together and move with the same post-collision
speed to be an extreme example of an inelastic
collision.
Now we will consider the analysis of a collision in which
the two objects do not stick together. In this collision, the
two objects will bounce off each other. While this is not
technically an elastic collision, it is more elastic than
collisions in which the two objects stick together
A 3000-kg truck moving with a velocity of 10 m/s
hits a 1000-kg parked car. The impact causes
the 1000-kg car to be set in motion at 15 m/s.
Assuming that momentum is conserved during
the collision, determine the velocity of the truck
after the collision. In this collision, the truck has
a considerable amount of momentum before the
collision and the car has no momentum (it is at
rest). After the collision, the truck slows down
(loses momentum) and the car speeds up (gains
momentum).
The collision can be analyzed using a momentum table
similar to the above situations.
Before Collision
After Collision
Truck
3000 * 10 = 30 000
3000 * v
Car
0
1000 * 15 = 15 000
Total
30 000
30 000
Observe in the table above that the known information
about the mass and velocity of the truck and car was
used to determine the before-collision momenta of the
individual objects and the total momentum of the system.
Since momentum is conserved, the total momentum
after the collision is equal to the total momentum before
the collision. The after-collision velocity of the car is used
(in conjunction with its mass) to determine its momentum
after the collision. Finally, the expression "3000*v" was
used for the after-collision momentum of the truck (v is
the velocity of the truck after the collision). To solve the
problem for "v" (the velocity of the truck), set the sum of
the individual after-collision momentum of the two
objects equal to the total momentum. The following
equation results:
3000*v + 15 000 = 30 000
3000*v = 15 000
v = 5.0 m/s
Using algebra skills, it can be shown that v = 5.0 m/s.
The truck's velocity immediately after the collision is 5.0
m/s. As predicted, the truck has slowed down (lost
momentum) and the car has gained momentum.
The three problems above illustrate how the law of
momentum conservation can be used to solve problems
in which the after-collision velocity of an object is
predicted based on mass-velocity information. There are
additional practice problems (with accompanying
solutions) later in this lesson which are worth the
practice. However, be certain that you don't come to
believe that physics is merely an applied mathematics
course which is devoid of concepts. For certain,
mathematics is applied in physics; however, physics is
about concepts and the variety of means in which they
are represented. Mathematical representations are just
one of the many representations of physics concepts.
Avoid merely treating these collision problems as mere
mathematical exercises. Take the time to understand the
concept of momentum conservation which provides the
basis of their solution.
Preview of What’s Ahead!
The next section of this lesson involves examples of
problems which provide a real test of your conceptual
understanding of momentum conservation in collisions.
Before proceeding with the practice problems, be sure to
try a few of the more conceptual questions which follow.
Using Equations as a Guide to
Thinking
The three problems on the previous page
illustrate how the law of momentum conservation
can be used to solve problems in which the
after-collision velocity of an object is predicted
based on mass-velocity information. There are
similar practice problems (with accompanying
solutions) lower on this page which are worth
the practice. However, let's first take a more
cognitive approach to some collision problems.
The questions which follow provide a real test of
your conceptual understanding of momentum
conservation in collisions.
A large fish is in motion at 2 m/s when it encounters a
smaller fish which is at rest. The large fish swallows the
smaller fish and continues in motion at a reduced speed.
If the large fish has three times the mass of the smaller
fish, then what is the speed of the large fish (and the
smaller fish) after the collision? Depress mouse on "popup menu" to view answer
Fishy Answer
The amount of mass in motion increased from 3m to 4 m
(3m + m). That is mass is increased by a factor of 4/3. To
conserve momentum, an increase in mass by a factor of
1.333 must be accompanied by decrease in the velocity
by a factor of 1.333. Divide the original velocity (2 m/s by
1.333).
V = 1.5 m/s
Conservation of Momentum
The Law of Action-Reaction
Revisited
An Introduction
A collision is an interaction between two objects which
have made contact (usually) with each other. As in any
interaction, a collision results in a force being applied to
the two colliding objects. Such collisions are governed by
Newton's laws of motion. In the past, Newton's third law
of motion was introduced and discussed. It was said
that...
... in every interaction, there is a pair of forces acting on
the two interacting objects. The size of the force on the
first object equals the size of the force on the second
object. The direction of the force on the first object is
opposite to the direction of the force on the second
object. Forces always come in pairs - equal and opposite
action-reaction force pairs.
Newton's third law of motion is naturally applied to
collisions between two objects. In a collision between
two objects, both objects experience forces which are
equal in magnitude and opposite in direction. Such
forces cause one object to speed up (gain momentum)
and the other object to slow down (lose momentum).
According to Newton's third law, the forces on
the two objects are equal in magnitude. While
the forces are equal in magnitude and opposite
in direction, the acceleration of the objects are
not necessarily equal in magnitude. In accord
with Newton's second law of motion, the
acceleration of an object is dependent upon both
force and mass. Thus, if the colliding objects
have unequal mass, they will have unequal
accelerations as a result of the contact force
which results during the collision.
Consider the collision between the club head and the
golf ball in the sport of golf. When the club head of a
moving golf club collides with a golf ball at rest upon a
tee, the force experienced by the club head is equal to
the force experienced by the golf ball. Most observers of
this collision have difficulty with this concept because
they perceive the high speed given to the ball as the
result of the collision
They are not observing unequal forces upon the
ball and club head, but rather unequal
accelerations. Both club head and ball
experience equal forces, yet the ball
experiences a greater acceleration due to its
smaller mass. In a collision, there is a force on
both objects which causes an acceleration of
both objects; the forces are equal in magnitude
and opposite in direction, yet the least massive
object receives the greatest acceleration.
Consider the collision between a moving seven-ball and
an eight-ball that is at rest in the sport of billiards. When
the seven-ball collides with the eight-ball, each ball
experiences an equal force directed in opposite
directions. The rightward moving seven-ball experiences
a leftward force which causes it to slow down; the eightball experiences a rightward force which causes it to
speed up
Since the two balls have equal masses, they will also
experience equal accelerations. In a collision, there is a
force on both objects which causes an acceleration of
both objects; the forces are equal in magnitude and
opposite in direction. For collisions between equal-mass
objects, each object experiences the same acceleration.
Consider the interaction between a male and
female figure skater in pair figure skating. A
woman (m = 45 kg) is kneeling on the shoulders
of a man (m = 70 kg); the pair is moving along
the ice at 1.5 m/s. The man gracefully tosses the
woman forward through the air and onto the ice.
The woman receives the forward force and the
man receives a backward force. The force on
the man is equal in magnitude and opposite in
direction to the force on the woman. Yet the
acceleration of the woman is greater than the
acceleration of the man due to the smaller mass
of the woman.
Many observers of this interaction have difficulty
believing that the man experienced a backward force.
"After all," they might argue, "the man did not move
backward." Such observers are presuming that forces
cause motion; that is a backward force would cause a
backward motion. This is a common misconception that
has been addressed before in our class.
Forces cause acceleration, not motion. The male figure
skater experiences a backwards (you might say
"negative") force which causes his backwards (or
"negative") acceleration; that is, the man slowed down
while the woman sped up. In every interaction (with no
exception), there are forces acting upon the two
interacting objects which are equal in magnitude and
opposite in direction.
Collisions are governed by Newton's laws. The law of
action-reaction (Newton's third law) explains the nature
of the forces between the two interacting objects.
According to the law, the force exerted by object 1 upon
object 2 is equal in magnitude and opposite in direction
to the force exerted by object 2 upon object 1.
Examples for you to try
Hint: Some of these questions could be seen
again!
1. While driving down the road, Anna Litical observed a
bug striking the windshield of her car. Quite obviously, a
case of Newton's third law of motion. The bug hit the
windshield and the windshield hit the bug. Which of the
two forces is greater: the force on the bug or the force on
the windshield?
Answer 1
TRICK Question! Each force is the same size.
For every action there is an equal (yes equal) reaction.
The fact that the bug splatters only means that it has a
smaller mass that was unable to withstand the larger
acceleration resulting from the interaction.
2. Rockets are unable to accelerate in space
because ...
A. there is no air in space for the rockets to push off
of.
B. there is no gravity is in space.
C. there is no air resistance in space.
D. ...nonsense! Rockets do accelerate in space.
Answer 2
Answer is D
It is a common misconception that rockets are unable to
accelerate in space. The fact is that rockets do
accelerate. They are able to accelerate due to the fact
that they burn fuel and push the exhaust in a direction
opposite to the direction they wish to accelerate.
3. A gun recoils when it is fired. The recoil is the
result of action-reaction force pairs. As the gases
from the gunpowder explosion expand, the gun
pushes the bullet forwards and the bullet pushes
the gun backwards. The acceleration of the
recoiling gun is ...
A. greater than the acceleration of the bullet.
B. smaller than the acceleration of the bullet.
C. the same size as the acceleration of the bullet.
Answer 3.
The answer is B.
The force on the gun equals the force on the bullet. Yet
acceleration depends on both force and mass. The bullet
has greater acceleration due to the fact that it has a
smaller mass. Remember acceleration and mass are
inversely proportional.
4. Why is it important that an airplane wing be designed
so that it deflects oncoming air downward?
Answer 4
This can be explained by Newton’s third law of motion.
The more air that a wing can push down, the more that
the air is able to push the wing up. If enough air is
pushed downward, then the reaction to this will result in
sufficient upward push on the wing and the plane to
provide the lift necessary to elevate the plane off the
ground.
5. Would it be a good idea to jump from a rowboat to a
dock that seems within jumping distance? Explain.
Answer 5
NO! Don’t do this at home (at least, not if you wish to
dock the boat)! As you jump to reach the dock, the
rowboat pushes you forward (action), and thus you push
the rowboat backwards. You will indeed reach the dock;
your rowboat will be several feet away!
6. If we throw a ball horizontally while standing on roller
skates, we roll backward with a momentum that matches
that of the ball. Will we roll backward if we go through the
motion of throwing the ball without letting go of it?
Explain.
Answer 6
The overall motion of a person who merely goes through
the motion of throwing the ball (without letting go) will be
“null.” Such a person will roll backwards then forwards.
Yet when finished the person will finish where she
started. Recall the demonstration of this in class.
Astronaut Description
We’ll look at an explanation then one more
example.
Imagine that you are hovering next to the space shuttle
in earth-orbit and your buddy of equal mass who is
moving 4 m/s (with respect to the ship) bumps into you.
If she holds onto you, then how fast do the two of you
move after the collision?
A question like this involves momentum principles. In any
instance in which two objects collide and can be
considered isolated from all other net forces, the
conservation of momentum principle can be utilized to
determine the post-collision velocities of the two objects.
Collisions between objects are governed by laws of
momentum and energy.
When a collision occurs in an isolated system, the total
momentum of the system of objects is conserved.
Provided that there are no net external forces acting
upon the two astronauts, the combined momentum of
the two astronauts before the collision equals the
combined momentum of the two astronauts after the
collision.
The mathematics of this problem is simplified by
the fact that before the collision, there is only
one object in motion and after the collision both
objects have the same velocity. That is to say, a
momentum analysis would show that all the
momentum was concentrated in the moving
astronaut before the collision. And after the
collision, all the momentum was the result of a
single object (the combination of the two
astronauts) moving at an easily predictable
velocity. Since there is twice as much mass in
motion after the collision, it must be moving at
one-half the velocity. Thus, the two astronauts
move together with a velocity of 2 m/s after the
collision.
7. Suppose there are three astronauts outside a
spaceship and two of them decide to play catch
with the other woman. All three astronauts weigh
the same on Earth and are equally strong. The
first astronaut throws the second astronaut
towards the third astronaut and the game
begins. Describe the motion of these women as
the game proceeds. Assume each toss results
from the same-sized "push." How long will the
game last?
Answer 7
The game will last two throws and one catch.
When astronaut #1 throws astronaut #2, the two
astronauts will travel opposite directions at the
same speed (action-reaction). When astronaut
#3 catches astronaut #2, astronaut #2 will slow
to half of her speed and move together with
astronaut #3. Now astronaut #1 is moving
leftward with original speed of astronaut #2 and
#3 are moving rightward at half of the original
speed. When astronaut #3 pushes #2, the
greatest speed which #2 can have is half of the
original speed in the opposite direction. The
game is now over for astronaut #2 can never
catch up with astronaut #1.
Conservation of Momentum
Momentum Conservation Principle
One of the most powerful laws in physics is the law of
momentum conservation. The law of momentum
conservation can be stated as follows.
For a collision occurring between object 1 and object 2 in
an isolated system, the total momentum of the two
objects before the collision is equal to the total
momentum of the two objects after the collision. That is,
the momentum lost by object 1 is equal to the
momentum gained by object 2.
The above statement tells us that the total momentum of
a collection of objects (a system) is conserved" - that is
the total amount of momentum is a constant or
unchanging value. This law of momentum conservation
will be the focus of the remainder of Lesson 2. To
understand the basis of momentum conservation, let's
begin with a short logical proof.
Consider a collision between two objects - object 1 and
object 2. For such a collision, the forces acting between
the two objects are equal in magnitude and opposite in
direction (Newton's third law). This statement can be
expressed in equation form as follows.
The forces act between the two objects for a
given amount of time. In some cases, the time is
long; in other cases the time is short. Regardless
of how long the time is, it can be said that the
time that the force acts upon object 1 is equal to
the time that the force acts upon object 2. This is
merely logical; forces result from interactions (or
touching) between two objects. If object 1
touches object 2 for 0.050 seconds, then object
2 must be touching object 1 for the same
amount of time (0.050 seconds). As an equation,
this can be stated as
Since the forces between the two objects are equal in
magnitude and opposite in direction, and since the times
for which these forces act are equal in magnitude, it
follows that the impulses experienced by the two objects
are also equal in magnitude and opposite in direction. As
an equation, this can be stated as
But the impulse experienced by an object is equal to the
change in momentum of that object (the impuslemomentum change theorem). Thus, since each object
experiences equal and opposite impulses, it follows
logically that they must also experience equal and
opposite momentum changes. As an equation, this can
be stated as
The above equation is one statement of the law of
momentum conservation. In a collision, the momentum
change of object 1 is equal and opposite to the
momentum change of object 2. That is, the momentum
lost by object 1 is equal to the momentum gained by
object 2.
In a collision between two objects, one object
slows down and loses momentum while the
other object speeds up and gains momentum. If
object 1 loses 75 units of momentum, then
object 2 gains 75 units of momentum. Yet, the
total momentum of the two objects (object 1 plus
object 2) is the same before the collision as it is
after the collision; the total momentum of the
system (the collection of two objects) is
conserved.
A useful analogy for understanding momentum
conservation involves a money transaction between two
people. Let's refer to the two people as Jack and Jill.
Suppose that we were to check the pockets of Jack and Jill
before and after the money transaction in order to
determine the amount of money which each possessed.
Prior to the transaction, Jack possesses $100 and Jill
possesses $100. The total amount of money of the two
people before the transaction is $200. During the
transaction, Jack pays Jill $50 for the given item being
bought. There is a transfer of $50 from Jack's pocket to
Jill's pocket. Jack has lost $50 and Jill has gained $50. The
money lost by Jack is equal to the money gained by Jill.
After the transaction, Jack now has $50 in his pocket and
Jill has $150 in her pocket. Yet, the total amount of money
of the two people after the transaction is $200. The total
amount of money (Jack's money plus Jill's money) before
the transaction is equal to the total amount of money after
the transaction. It could be said that the total amount of
money of the system (the collection of two people) is
conserved; it is the same before as it is after the
transaction.
A useful means of depicting the transfer and the
conservation of money between Jack and Jill is by
means of a table.
The table shows the amount of money possessed by the
two individuals before and after the interaction. It also
shows the total amount of money before and after the
interaction. Note that the total amount of money ($200) is
the same before and after the interaction - it is
conserved. Finally, the table shows the change in the
amount of money possessed by the two individuals. Note
that the change in Jack's money account (-$50) is equal
and opposite to the change in Jill's money account
(+$50) .
Virtual Lab
Truck and Brick Lab
Collisions between objects are governed by laws
of momentum and energy. When a collision
occurs in an isolated system, the total
momentum of the system of objects is
conserved. Provided that there are no net
external forces acting upon the objects, the
momentum of all objects before the collision
equals the momentum of all objects after the
collision. If there are only two objects involved in
the collision, then the momentum lost by one
object equals the momentum gained by the
other object
The animation below portrays the collision
between a 3.0-kg loaded cart and a 2-kg
dropped brick. It will be assumed that there are
no net external forces acting upon the two
objects involved in the collision. The only net
force acting upon the two objects (loaded cart
and dropped brick) are internal forces - the force
of friction between the loaded cart and the
droped brick. The before- and after-collision
velocities and momentum are shown in the data
tables.
In the collision between the loaded cart and the
dropped brick, total system momentum is
conserved. Before the collision, the momentum
of the loaded cart is 150 kg*cm/s and the
momentum of the dropped brick is 0 kg*cm/s; the
total system momentum is 150 kg*cm/s. After the
collision, the momentum of the loaded cart is
90.0 kg*cm/s and the momentum of the dropped
brick is 60.0 kg*cm/s; the total system
momentum is 150 kg*cm/s. The momentum of
the loaded cart-dropped brick system is
conserved. The momentum lost by the loaded
cart (60 kg*cm/s) is gained by the dropped brick
1 kg cart and 2 kg brick
In the collision between the cart and the dropped
brick, total system momentum is conserved.
Before the collision, the momentum of the cart is
60 kg*cm/s and the momentum of the dropped
brick is 0 kg*cm/s; the total system momentum is
60 kg*cm/s. After the collision, the momentum of
the cart is 20.0 kg*cm/s and the momentum of
the dropped brick is 40.0 kg*cm/s; the total
system momentum is 60 kg*cm/s. The
momentum of the loaded cart-dropped brick
system is conserved. The momentum lost by the
loaded cart (40 kg*cm/s) is gained by the
dropped brick.
For any collision occurring in an isolated system,
momentum is conserved - the total amount of
momentum of the collection of objects in the system is
the same before the collision as after the collision. This
is the very phenomenon which was observed in "The
Cart and The Brick" lab. In this lab, a brick at rest was
dropped upon a loaded cart which was in motion.
Cart and Brick Lab
Before the collision, the dropped brick had 0 units of
momentum (it was at rest). The momentum of the loaded
cart can be determined using the velocity (as determined
by the ticker tape analysis) and the mass. The total
amount of momentum was the sum of the dropped brick's
momentum (0 units) and the loaded cart's momentum.
After the collision, the momenta of the two separate
objects (dropped brick and loaded cart) can be
determined from their measured mass and their velocity
(found from the ticker tape analysis). If momentum is
conserved during the collision, then the sum of the
dropped brick's and loaded cart's momentum after the
collision should be the same as before the collision. The
momentum lost by the loaded cart should equal (or
approximately equal) the momentum gained by the
dropped brick.
Momentum data for the interaction between the dropped brick and the loaded cart
could be depicted in a table similar to the money table above.
Before
Collision
Momentum
After
Collision
Momentum
Change in
Momentum
Dropped Brick
0 units
14 units
+14 units
Loaded Cart
45 units
31 units
-14 units
Total
45 units
45 units
Note that the loaded cart lost 14 units of momentum and
the dropped brick gained 14 units of momentum. Note
also that the total momentum of the system (45 units)
was the same before the collision as it is after the
collision.
Collisions commonly occur in contact sports
(such as football) and racket and bat sports
(such as baseball, golf, tennis, etc.). Consider a
collision in football between a fullback and a
linebacker during a goal-line stand. The fullback
plunges across the goal line and collides in
midair with linebacker. The linebacker and
fullback hold each other and travel together after
the collision. The fullback possesses a
momentum of 100 kg*m/s, East before the
collision and the linebacker possesses a
momentum of 120 kg*m/s, West before the
collision. The total momentum of the system
before the collision is 20 kg*m/s, West (review
the section on adding vectors if necessary).
Therefore, the total momentum of the system
after the collision must also be 20 kg*m/s, West.
The fullback and the linebacker move together
as a single unit after the collision with a
combined momentum of 20 kg*m/s. Momentum
is conserved in the collision. A vector diagram
can be used to represent this principle of
momentum conservation; such a diagram uses
an arrow to represent the magnitude and
direction of the momentum vector for the
individual objects before the collision and the
combined momentum after the collision.
Now suppose that a medicine ball is thrown to a clown
who is at rest upon the ice; the clown catches the
medicine ball and glides together with the ball across the
ice. The momentum of the medicine ball is 80 kg*m/s
before the collision. The momentum of the clown is 0 m/s
before the collision. The total momentum of the system
before the collision is 80 kg*m/s. Therefore, the total
momentum of the system after the collision must also be
80 kg*m/s. The clown and the medicine ball move
together as a single unit after the collision with a
combined momentum of 80 kg*m/s. Momentum is
conserved in the collision.
Momentum is conserved for any interaction between two
objects occurring in an isolated system. This
conservation of momentum can be observed by a total
system momentum analysis and by a momentum
change analysis. Useful means of representing such
analyses include a momentum table and a vector
diagram. Later in Lesson 2, we will use the momentum
conservation principle to solve problems in which the
after-collision velocity of objects is predicted.
Examples
1. Explain why it is difficult for a firefighter to hold a hose
which ejects large amounts of high-speed water.
Answer 1
The hose is pushing lots of water (large mass) forward at
a high speed. This means that the water has a huge
forward momentum. In turn, the hose must have an
equally large backwards momentum, making it difficult
for firefighters to manage.
2. A large truck and a Volkswagen have a headon collision.
a. Which vehicle experiences the greatest force
of impact?
b. Which vehicle experiences the greatest
impulse?
c. Which vehicle experiences the greatest
momentum change?
d. Which vehicle experiences the greatest
acceleration?
Answer 2
A , b, c, same answer for all
Both the Volkswagen and the large truck
encounter the same force, the same impulse,
and the same momentum change.
D. Acceleration is greatest for the Volkswagen.
While the two vehicles experience the same
force, the acceleration is greatest for the
Volkswagen which has the smaller mass. If you
find this hard believe then read the next question
and its accompanying explanation.
3. Miles Tugo and Ben Travlun are riding in a
bus at highway speed on a nice summer day
when an unlucky bug splatters onto the
windshield. Miles and Ben begin discussing the
physics of the situation. Miles suggests that the
momentum change of the bug is much greater
than that of the bus. After all, argues Miles, there
was no noticeable change in the speed of the
bus compared to the obvious change in the
speed of the bug. Ben disagrees entirely,
arguing that that both bug and bus encounter
the same force, momentum change, and
impulse. Who do you agree with? Support your
answer
Answer 3
Ben Travelun is correct. The bug and bus
experience the same force, same impulse and
the same momentum change. This is contrary to
popular (but false) belief which matches Miles’
statement. The bug has less mass and therefore
more acceleration; occupants of the very
massive bus do not feel the extremely small
acceleration. Furthermore, the bug is composed
of a less hardy material and thus splatters all
over the windshield. Yet the greater
splatterability of the bug and the greater
acceleration do not mean that the bug has a
greater force, impulse, or momentum change.
4. If a ball is projected upward from the ground with ten
units of momentum, what is the momentum of recoil of
the Earth? ____________ Do we feel this? Explain.
Answer 4
The earth recoils with 10 units of momentum. This is not
felt by Earth’s occupants. Since the mass of the Earth is
extremely large, the recoil velocity of the Earth is
extremely small and therefore not felt
5. If a 5-kg bowling ball is projected upward with a
velocity of 2.0 m/s, then what is the recoil velocity of the
Earth (mass = 6.0 x 10^24 kg).
Answer 5
Since the ball has an upward momentum of 10 kg m/s,
the Earth must have a downward momentum of 10 kg
m/s. To find the velocity of the Earth, use the momentum
equation p = m * v. This equation rearranges to v = p/m.
By substituting into this equation
v = (10 kg m/s) / (6 x 10 24 kg).
V = 1.67 * 10 -24 m/s (downward)
6. A 120 kg lineman moving west at 2 m/s tackles an 80
kg football fullback moving east at 8 m/s. After the
collision, both players move east at 2 m/s. Draw a vector
diagram in which the before- and after-collision momenta
of each player is represented by a momentum vector.
Label the magnitude of each momentum vector.
Answer 6
7. Would you care to fire a rifle that has a bullet ten times
as massive as the rifle? Explain.
Answer 7
Absolutely not! In a situation like this, the target would be
a safer place to stand than the rifle. The rifle would have
recoil velocity that is ten times larger than the bullet’s
velocity. This would produce the effect of “the rifle
actually being the bullet.”
8. A baseball player holds a bat loosely and bunts a ball.
Express your understanding of momentum conservation
by filling in the tables below.
Answer 8
A) + 40 (add momentum of ball and bat)
C) + 40 (momentum must be conserved)
B) + 30 (the bat must have 30 units of momentum in
order in order for the total to be +40)
9. A Tomahawk cruise missile is launched from the barrel
of a mobile missile launcher. Neglect friction. Express
your understanding of momentum conservation by filling
in the tables below.
Answer 9
A) 0 (add the momentum of the missile and launcher)
C) 0 (the momentum is the same after as it is before the
collision)
B) -5000 (the launcher must have -5000 units of
momentum in order for the total to be zero)
Momentum—Real World
Looking Back
In a previous part of Lesson 1, it was said that
In a collision, an object experiences a force for a given
amount of time which results in its mass undergoing a
change in velocity (i.e., which results in a momentum
change).
What do we get from this?
There are four physical quantities mentioned in the
above statement - force, time, mass, and velocity
change. The force multiplied by the time is known as the
impulse and the mass multiplied by the velocity change
is known as the change in momentum. The impulse
experienced by an object is always equal to the change
in its momentum. In terms of equations, this was
expressed as (eqn on next slide)
Equations
This is known as the impulse-momentum change
theorem.
In this part of Lesson 1, we will examine some realworld applications of the impulse-momentum change
theorem. We will examine some physics in action in the
real world. In particular, we will focus upon 2 ideas….
Real World Applications
the effect of collision time upon the amount of force an
object experiences, and
the effect of rebounding upon the velocity change and
hence the amount of force an object experiences
As an effort is made to apply the impulse-momentum
change theorem to a variety of real-world situations,
keep in mind that the attempt is to use the equation as a
guide to thinking about how an alteration in the value of
one variable might effect the value of another variable.
Effect of Collision Time on Force
As an effort is made to apply the impulse-momentum
change theorem to a variety of real-world situations,
keep in mind that the attempt is to use the equation as a
guide to thinking about how an alteration in the value of
one variable might effect the value of another variable.
Combinations of Force and Time Required to Produce 100
units of Impulse
Force
Time
Impulse
100
1
100
50
2
100
25
4
100
10
10
100
4
25
100
2
50
100
1
100
100
0.1
1000
100
Observe that the greater the time over which the collision
occurs, the smaller the force acting upon the object.
Thus, to minimize the effect of the force on an object
involved in a collision, the time must be increased; and
to maximize the effect of the force on an object involved
in a collision, the time must be decreased.
There are several real-world applications of this
phenomena. One example is the use of air bags in
automobiles. Air bags are used in automobiles because
they are able to minimize the effect of the force on an
object involved in a collision. Air bags accomplish this by
extending the time required to stop the momentum of the
driver and passenger. When encountering a car collision,
the driver and passenger tend to keep moving in accord
with Newton's first law. Their motion carries them
towards a windshield which results in a large force
exerted over a short time in order to stop their
momentum. If instead of hitting the windshield, the driver
and passenger hit an air bag, then the time duration of
the impact is increased. When hitting an object with
some give such as an air bag, the time duration might be
increased by a factor of 100. Increasing the time by a
factor of 100 will result in a decrease in force by a factor
of 100. Now that's physics in action.
There are several real-world applications of this
phenomena. One example is the use of air bags in
automobiles. Air bags are used in automobiles because
they are able to minimize the effect of the force on an
object involved in a collision. Air bags accomplish this by
extending the time required to stop the momentum of the
driver and passenger. When encountering a car collision,
the driver and passenger tend to keep moving in accord
with Newton's first law. Their motion carries them towards
a windshield which results in a large force exerted over a
short time in order to stop their momentum. If instead of
hitting the windshield, the driver and passenger hit an air
bag, then the time duration of the impact is increased.
When hitting an object with some give such as an air bag,
the time duration might be increased by a factor of 100.
Increasing the time by a factor of 100 will result in a
decrease in force by a factor of 100. Now that's physics in
action.
Fans of boxing frequently observe this same principle of
minimizing the effect of a force by extending the time of
collision. When a boxer recognizes that he will be hit in
the head by his opponent, the boxer often relaxes his
neck and allows his head to move backwards upon
impact. In the boxing world, this is known as riding the
punch. A boxer rides the punch in order to extend the
time of impact of the glove with their head. Extending the
time results in decreasing the force and thus minimizing
the effect of the force in the collision. Merely increasing
the collision time by a factor of ten would result in a
tenfold decrease in the force. Now that's physics in
action.
Nylon ropes are used in the sport of rock-climbing for the
same reason. Rock climbers attach themselves to the
steep cliffs by means of nylon ropes. If a rock climber
should lose her grip on the rock, she will begin to fall. In
such a situation, her momentum will ultimately be halted
by means of the rope, thus preventing a disastrous fall to
the ground below. The ropes are made of nylon or
similar material because of its ability to stretch. If the
rope is capable of stretching upon being pulled taut by
the falling climber's mass, then it will apply a force upon
the climber over a longer time period. Extending the time
over which the climber's momentum is broken results in
reducing the force exerted on the falling climber. For
certain, the rock climber can appreciate minimizing the
effect of the force through the use of a longer time of
impact. Now that's physics in action.
In racket and bat sports, hitters are often encouraged
to follow-through when striking a ball. High speed
films of the collisions between bats/rackets and balls
have shown that the act of following through serves
to increase the time over which a collision occurs.
This increase in time must result in a change in
some other variable in the impulse-momentum
change theorem. Surprisingly, the variable which is
dependent upon the time in such a situation is not
the force. The force in hitting is dependent upon how
hard the hitter swings the bat or racket, not the time
of impact. Instead, the follow-through increases the
time of collision and subsequently contributes to an
increase in the velocity change of the ball. By
following through, a hitter can hit the ball in such a
way that it leaves the bat or racket with more velocity
(i.e., the ball is moving faster). In tennis, baseball,
racket ball, etc., giving the ball a high velocity often
leads to greater success. Now that's physics in
action.
A water balloon was thrown high into the air and
successfully caught (i.e., caught without breaking). The
key to the success of the demonstration was to contact
the ball with outstretched arms and carry the ball for a
meter or more before finally stopping its momentum. The
effect of this strategy was to extend the time over which
the collision occurred and so reduce the force. This
same strategy is used by lacrosse players when catching
the ball. The ball is "cradled" when caught; i.e., the
lacrosse player reaches out for the ball and carries it
inward toward her body as if she were cradling a baby.
The effect of this strategy is to lengthen the time over
which the collision occurs and so reduce the force on the
lacrosse ball. Now that's physics in action.
Another memorable in-class demonstration was the
throwing of an egg into a bed sheet. The bed sheet was
held by two trustworthy students and our best pitcher (so
we thought) was used to toss the egg at full speed into
the bed sheet. The collision between the egg and the bed
sheet lasts over an extended period of time since the bed
sheet has some give in it. By extending the time of the
collision, the effect of the force is minimized. In all my
years, the egg has never broken when hitting the bed
sheet. On the other hand, it seems that every year there
is a pitcher who is not as accurate as we expected. The
pitcher misses the bed sheet and collides with the board.
In these unexpected cases, the collision between
whiteboard and egg lasts for a short period of time, thus
maximizing the effect of the force on the egg. The egg
brakes and leaves the whiteboard and floor in a
considerable mess. And that's no yolk!
Effect of Rebounding
Occasionally when objects collide, they bounce
off each other (as opposed to sticking to each
other and traveling with the same speed after
the collision). Bouncing off each other is known
as rebounding. Rebounding involves a change
in direction of an object; the before- and aftercollision direction is different. Rebounding was
pictured and discussed earlier in Lesson 1. At
that time, it was said that rebounding situations
are characterized by a large velocity change and
a large momentum change.
From the impulse-momentum change theorem, we could
deduce that a rebounding situation must also be
accompanied by a large impulse. Since the impulse
experienced by an object equals the momentum change
of the object, a collision characterized by a large
momentum change must also be characterized by a
large impulse.
The importance of rebounding is critical to the outcome
of automobile accidents. In an automobile accident, two
cars can either collide and bounce off each other or
collide and crumple together and travel together with the
same speed after the collision. But which would be more
damaging to the occupants of the automobiles - the
rebounding of the cars or the crumpling up of the cars?
Contrary to popular opinion, the crumpling up of cars is
the safest type of automobile collision. As mentioned
above, if cars rebound upon collision, the momentum
change will be larger and so will the impulse. A greater
impulse will typically be associated with a bigger force.
Occupants of automobiles would certainly prefer small
forces upon their bodies during collisions.
In fact, automobile designers and safety engineers
have found ways to reduce the harm done to
occupants of automobiles by designing cars which
crumple upon impact. Automobiles are made with
crumple zones. Crumple zones are sections in
cars which are designed to crumple up when the
car encounters a collision. Crumple zones
minimize the effect of the force in an automobile
collision in two ways. By crumpling, the car is less
likely to rebound upon impact, thus minimizing the
momentum change and the impulse. Finally, the
crumpling of the car lengthens the time over which
the car's momentum is changed; by increasing the
time of the collision, the force of the collision is
greatly reduced.