* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download PPT - Henry Haselgrove`s Homepage
Measurement in quantum mechanics wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Density matrix wikipedia , lookup
Quantum dot wikipedia , lookup
Path integral formulation wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Renormalization group wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Coherent states wikipedia , lookup
Quantum field theory wikipedia , lookup
Quantum fiction wikipedia , lookup
Renormalization wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Scalar field theory wikipedia , lookup
Hydrogen atom wikipedia , lookup
Particle in a box wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Bell's theorem wikipedia , lookup
Quantum computing wikipedia , lookup
EPR paradox wikipedia , lookup
Quantum machine learning wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Orchestrated objective reduction wikipedia , lookup
Quantum group wikipedia , lookup
Quantum key distribution wikipedia , lookup
Quantum teleportation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
History of quantum field theory wikipedia , lookup
Quantum state wikipedia , lookup
Quantum cognition wikipedia , lookup
Canonical quantization wikipedia , lookup
GRIFFITH QUANTUM THEORY SEMINAR
10 NOVEMBER 2003
Entanglement, correlation, and errorcorrection in the ground states of manybody systems
Henry Haselgrove
School of Physical Sciences
University of Queensland
Michael Nielsen - UQ
Tobias Osborne – Bristol
Nick Bonesteel – Florida State
quant-ph/0308083
quant-ph/0303022 – to appear in PRL
When we make basic assumptions about the
interactions in a multi-body quantum system,
what are the implications for the ground state?
Basic assumptions --- simple general assumptions
of physical plausibility, applicable to most
physical systems.
Nature gets by with just 2-body interactions
Far-apart
things don’t directly interact
Implications for the ground state --- using the
concepts of Quantum Information Theory.
Error-correcting
properties
Entanglement properties
Why ground states are really cool
Physically, ground states are interesting:
T=0 is only thermal state that can be a pure
state (vs. mixed state)
Pure states are the “most quantum”.
Physically: superconductivity, superfluidity,
quantum hall effect, …
Ground states in Quantum Information
Processing:
Naturally
fault-tolerant systems
Adiabatic quantum computing
Part 1: Two-local interactions
N interacting quantum
systems, each d-level
Interactions may only
be one- and two-body
Consider the whole
state space. Which
of these states are
the ground state of
some (nontrivial)
two-local
Hamiltonian?
1
3
2
4
…
N
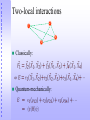
Two-local interactions
2
1
4
3
Classically:
Quantum-mechanically:
Two-local Hamiltonians
N quantum bits, for clarity
Any imaginable Hamiltonian is a real linear
combination of basis matrices An,
{An} = All N-fold tensor products of Pauli matrices,
Any two-local Hamiltonian is written as
where the Bn are N-fold tensor products of Pauli
matrices with no more than two non-identity terms.
Example
is two-local, but
is not.
Why two-locality restricts ground states: parameter counting
argument
2
O(N )
O(2N) parameters
Necessary condition for |> to be twolocal ground state
We have
and
Take E=0
Not interested in trivial case where all cn=0
So the set
must be linearly
dependent for |i to be a two-local ground state
Nondegenerate quantum
error-correcting codes
A state |> is in a QECC that corrects L errors if
in principle the original state can be recovered
after any unknown operation on L of the qubits
acts on |>
The {Bn} form a basis for errors on up to 2 qubits
A QECC that corrects two errors is nondegenerate
if each {Bn} takes |i to a mutually orthogonal
state
Only way you can have
is if all cn=0
) trivial Hamiltonian
A nondegenerate QECC can not be the eigenstate
of any nontrivial two-local Hamiltonian
In fact, it can not be even near an eigenstate of
any nontrivial two-local Hamiltonian
H = completely arbitrary nontrivial 2-local Hamiltonian
= nondegenerate QECC correcting 2 errors
E = any eigenstate of H (assume it has zero eigenvalue)
Want to show that these assumptions alone imply that
|| - E || can never get small
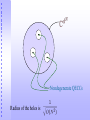
Nondegenerate QECCs
Radius of the holes is
Part 2: When far-apart objects
don’t interact
In the ground state, how much entanglement is there
between the ●’s?
We find that the entanglement is bounded by a
function of the energy gap between ground and first
exited states
Energy gap E1-E0:
Physical
quantity: how much energy is needed to excite to
higher eigenstate
Needs to be nonzero in order for zero-temperature state to
be pure
Adiabatic QC: you must slow down the computation
when the energy gap becomes small
Entanglement:
Uniquely
quantum property
A resource in several Quantum Information Processing
tasks
Is required at intermediate steps of a quantum
computation, in order for the computation to be powerful
Some related results
Theory of quantum phase transitions. At a QPT,
one sees both
a
vanishing energy gap, and
correlations in the ground state.
Theory usually applies to infinite quantum systems.
long-range
Non-relativistic Goldstone Theorem.
Diverging
correlations imply vanishing energy gap.
Applies to infinite systems, and typically requires
additional symmetry assumptions
Extreme case: maximum entanglement
A
B
C
Assume the ground state has maximum
entanglement between A and C
or
A
B
C
That is, whenever you have couplings of the form
A
B
C
it is impossible to have a unique ground state that
maximally entangles A and C.
So, a maximally entangled ground state implies a
zero energy gap
Same argument extends to any maximally
correlated ground state
Can we get any entanglement between A and
C in a unique ground state?
Yes. For example (A, B, C are spin-1/2):
0.1X
X
0.1X
= 0.1 (XX + YY + ZZ)
… has a unique ground state having an
entanglement of formation of 0.96
Can we prove a general trade-off
between ground-state entanglement
and the gap?
1.4000
1.0392
1.0000
0.6485
-1.0000
-1.0000
-1.0392
-1.0485
General result
A
B
C
Have a “target state” |i that we want “close” to
being the ground state |E0i
--- measure of closeness of target to ground
--- measure of correlation between A and C
The future…
At the moment, our bound on the energy gap
becomes very weak when you make the system
very large. Can we improve this?
The question of whether a state can be a unique
ground state is closely related to the question of
when a state is uniquely determined by its
reduced density matrices. Explore this question
further: what are the conditions for this “unique
extended state”?
Conclusions
Simple yet widely-applicable assumptions on
the interactions in a many-body quantum
system, lead to interesting and powerful results
regarding the ground states of those systems
1.
2.
Assuming two-locality affects the errorcorrecting abilities
Assuming that two parts don’t directly
interact, introduces a correlation-gap
trade-off.