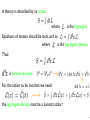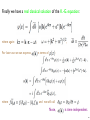* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Canonical quantization of scalar fields
BRST quantization wikipedia , lookup
Hydrogen atom wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Wave–particle duality wikipedia , lookup
History of quantum field theory wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
Perturbation theory wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Schrödinger equation wikipedia , lookup
Wave function wikipedia , lookup
Renormalization group wikipedia , lookup
Scale invariance wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Noether's theorem wikipedia , lookup
Path integral formulation wikipedia , lookup
Dirac equation wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Dirac bracket wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Canonical quantization wikipedia , lookup
Canonical quantization of scalar fields based on S-3 Hamiltonian for free nonrelativistic particles: Furier transform: a(x) = we get: ! d3 p ip·x e ã(p) ! 3/2 (2π) d3 x (2π)3 eip·x = δ 3 (p) can go back to x using: ! d3 p ip·x 3 e = δ (x) 3 (2π) 28 Canonical quantization of scalar fields (Anti)commutation relations: [A, B]∓ = AB ∓ BA Vacuum is annihilated by : is a state of momentum is eigenstate of , eigenstate of with with energy eigenvalue: 29 Relativistic generalization Hamiltonian for free relativistic particles: spin zero, but can be either bosons or fermions Is this theory Lorentz invariant? Let’s prove it from a different direction, direction that we will use for any quantum field theory from now: start from a Lorentz invariant lagrangian or action derive equation of motion (for scalar fields it is K.-G. equation) find solutions of equation of motion show the Hamiltonian is the same as the one above 30 A theory is described by an action: where is the lagrangian. Equations of motion should be local, and so where is the lagrangian density. Thus: is Lorentz invariant: For the action to be invariant we need: the lagrangian density must be a Lorentz scalar! 31 Any polynomial of a scalar field is a Lorentz scalar and so are products of derivatives with all indices contracted. Let’s consider: arbitrary constant ! = 1, c = 1 and let’s find the equation of motion, Euler-Lagrange equation: (we find eq. of motion from variation of an action: making an infinitesimal variation in and requiring the variation of the action to vanish) integration by parts, and δφ(x) = 0 at infinity in any direction (including time) is arbitrary function of x and so the equation of motion is Klein-Gordon equation 32 Solutions of the Klein-Gordon equation: one classical solution is a plane wave: is arbitrary real wave vector and The general classical solution of K-G equation: where and are arbitrary functions of , and is a function of |k| (introduced for later convenience) if we tried to interpret as a quantum wave function, the second term would represent contributions with negative energy to the wave function! 33 real solutions: k −→ −k thus we get: (such a k µ is said to be on the mass shell) 34 Finally let’s choose so that is Lorentz invariant: manifestly invariant under orthochronous Lorentz transformations on the other hand sum over zeros of g, in our case the only zero is k 0 = ω for any the differential it is convenient to take the Lorentz invariant differential is: is Lorentz invariant for which 35 Finally we have a real classical solution of the K.-G. equation: where again: For later use we can express where , , in terms of : and we will call Note, . is time independent. 36 Constructing the hamiltonian: Recall, in classical mechanics, starting with lagrangian as a function of coordinates and their time derivatives we define conjugate momenta and the hamiltonian is then given as: In field theory: hamiltonian density and the hamiltonian is given as: 37 In our case: Inserting we get: 38 ! d3 x ip·x e = δ 3 (p) 3 (2π) 39