Download Ground State

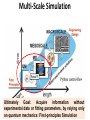
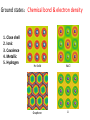
Introduction to Computational
Chemistry and Materials
武晓君 (Xiaojun Wu) [email protected]
江俊 (Jun Jiang) [email protected]
Question 1：Why Model and Simulation?
Conventional style for making new material
Try
Sample
Metallic Wire
Error
3 Years
Plant/Carbon Wire
Question 1：Why Model and Simulation?
After 130 years
New Style for New Material
Experiment
Theory
Simulation
photon
nucleus
electron
Material Characterization
at the atomic scale
TEM
transmission electron microscope
Spring with Carbon Nanotube
Life Science
Macroscopic view
Cell View
Single-molecue View
Chemical Reaction
Conventional reaction
State-State reaction
Single-molecule reaction
Single Atom/Molecule Manipulation
In Touch with Atoms
• AFM，STM，SPM
In Touch with Atoms
Quantum Corral
Controlled bond formation at
the spatial limit.
Science 286,1719(1999)
Growing Importance of Computational Modeling
Nuclear Reaction
Safeguarding the Nuclear Stockpile
through Computer Simulation
Supercomputers study reactor core behaviour
http://www.world-nuclear-news.org/nn-supercomputers_study_reactor_core_behaviour-2701104.html
Growing Importance of Computational Modeling
Calculating things that are difficult to do experimentally:
Inside the Earth
The melting curve of Iron at the pressures of the
Earth’s core from ab initio calculations.
Source: http://chianti.geol.ucl.ac.uk/~dario/resint.htm
Alfe’ et al , Nature 401, 462, (1999)
Growing Importance of Computational Modeling
First Principles Materials Modeling in Industry
Materials
Genome
Motorola IBM
Dynamics of vortices
Large-scale simulations of human
bone under elastic deformations
Siemens
Eastman Kodak
Phillips Xerox Electricité de
France Texas Instruments
Ford
Nippon Steel
Matsushita (Panasonic)
Ricoh
Allied Signal
Alcoa Toyota General Motors
TDK Lucent Hitachi Corning
http://www.zurich.ibm.com/mcs/compsci/engineering/vortices.html
Engine turbine Metal
Extreme Conditions:
3000K，10GPa
Engine turbine Metal
Metal melting
70,000 atoms(Al, Fe, Cu)
Engine turbine Metal
Metal melting : 70,000 atoms(Al, Fe, Cu)
Engine turbine Metal
Save: 43, 200, 000 RMB
Simulation cost: 200,000 RMB
Question 1：Why Model and Simulation?
Answer
• Understand complex systems, processes, and
phenomena
at
the
fundamental
and
quantitative level
• Bridge theory and experiment
• Wide
applications
in
Physics,
Chemistry,
Material, Life, Information science
What is Model and Simulation?
Model?
Simplified Description of Actual System
 Nuclei and electron (electronic-structure level)
 Atoms and molecules (atomistic or molecular)
 Coupled structural elements (finite-element)
 Medium described by fields and distributions (continuum)
Cu Crystal: potential U(r1, r2, …, rN)  various properties
How? Process to do this is Simulation
What is useful and key to a good model?
• The complex system can be simplified to
– Base structure Clear
– Interactions among particles Clear
 Key 1: What kind of models are employed to simplify
the systems?
 Key 2: What are the specific problems of the realistic
applications?
 Key 3: What are the limits of the models and methods?
Multi-Scale Simulation
Ultimately
Goal:
Acquire
information
without
experimental data or fitting parameters, by relying only
on quantum mechanics: First-principles Simulation
QM Simulation
Start with quantum mechanics and
electronic structure
Modern physics and chemistry applications rely on the
detection and manipulation of electron kinetics:
the space, time, energy information of electrons.
Energy
transfer
Photon/
Electron
Electronic(excited) states
generation and coupling
Material
Conversion
Movement and evolution
c.b. e
H2O
O2
Semicond
h+ v.b.
H+
CO2
H2
Gas
Photocatalysis
Mol-Photonics
Mol-Electronics
Optoelectronics
Catalysis
Photo-detector
Electronic structure decides material property
1890s Electron is a particle
1896
Pieter Zeeman, Lorentz “spectra line splitting” in magnetic filed
1902 Nobel Prize
1897
J J Thomson “Find electron in experiment “ negative charged
1906 Nobel Prize
1901
Rutherford
1911
Bohr
“Find positive charged nuclei” experimentally
Quantum Mechanics “discrete set of allowed levels of electrons”
De Brogil，Schrodinger， Heisenberg
Electron has spin
1925
Periodic Tablet
1926
Pauli exclusion theory “No two electrons at same Quantum State”
1927
Fermi Bose-Einstein Statistics
Electron
Electronic Structure : Molecular
Lewis 1916 JACS, 38, 762 “The atom and the molecule”
Electrons are delocalized over atoms
forming “Chemical Bond”
Electronic Structure : Condensed Matter
A system made of many particles (atoms, molecules, ions, …) which interacting
strongly with each other: Solid, Liquid, … ….
In principle: Many-body problem
Independent Particle Approximation
+： Fermi – Dirac Distribution
- ： Bose-Einstein Distribution
Occupation Number
Energy of Independent particle
Electronic Structure : Solid
Independent electron + periodic potential of crystal lattice
Wavefunction in solid is the eigenstate of “Crystal Momentum”
Electronic Band
Metal: Electrons move freely
 Insulator (Ionic , Valence，Molecular)
Semiconductor
Band Theory
Electronic Structure of Diamond
G.E.Kimball, J. Chem. Phys. 3:560， 1935
The first quantitative calculations of electronic states for Na metal
The firs quantitatively accurate calculations of bands in semiconductor Ge
Beyond the Independent Particle
Electron Correlation (Challenge)
What are results of electron correlation:
1. Magnetism: Exchange energy of interacting electrons
2. Metal-Insulator Transition: Many-body effects (1950s)
Developments:
• Advanced quantum chemistry method
• Density functional theory method
• Quantum Monte Carlo
• Dynamic Mean-field Theory
• Many-body perturbation
What we want to Know?
Electronic structure of ground and excited states
 Ground State
–
–
–
–
–
–
–
–
Cohesive energy
Crystal Structure
Phase transition
Elastic constant
Charge density
Magnetic property
Dielectric
Nuclear vibration and
motion
– Metal/Semiconductor/Insul
ator
– ……
 Excited State
– Low energy excitations
– Specific heat in metal
– Transport
– Pauli spin susceptibility
– High energy excitations
– Gap
– Optical properties
– Spectra for adding or
removing electrons
– ……
Ground states：Chemical bond & electron density
1.
2.
3.
4.
5.
Close shell
Ionic
Covalence
Metallic
Hydrogen
He Solid
NaCl
Graphene
Li
Electron density：atomic charge distribution
Si deformation charge density
Experimental measurement:
scattering of X-ray or High-energy electrons
Ground state：Volume & Pressure
Stable / equilibrium structure with volumn (Ω) under certain
pressure (P) and temperature (T) decide material properties
-14.2
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3
-14.4
-14.6
-14.8
-15
Series1
-15.2
-15.4
-15.6
-15.8
-16
Diamond
E .vs. lattice
Bulk modulus of 3d/4d transition metal
Pressure/stress induced phase transition
Free Energy
Gibbs free energy
Enthalpy H
Phase Transition Pressure/Stress
8GP
Energy vs. Volume
“an impressive
achievement of “firstprinciples” theory
with no adjustable
parameters？
Lowest transition pressure for tetrahedral semiconductors to a high-pressure phase
Ground state：Elasticity
Stress tensor
Strain
Isotropic material
Young’s Modulus
Poisson’s ratio
Bulk modulus
Shear modulus
Ground state：Magnetism
Many-body effect caused by electron-electron interaction
Open shell atoms
Hund’s rule: the ground state has the maximum total spin
and maximum orbital moment
Zeeman field Hzeeman = m(r) Vm(r)  exchange-correlation energy
Total Energy
Magnetic
susceptibility
Spin Charge Density Distribution
Graphene Piece
Ground state：Vibrational & phonon
Vibrational Spectra
Experimental: infrared absorption
Light scattering
inelastic neutron scattering
other…
RI
FI
CIJ
position of nuclei I
Force on nuclei I
Force constant
Usually, difference within experiments ~ 5%
Two methods:
1. “Frozen phonon”
direct calculation energy with atomic positions
2. “Response Function”
calculation of derivations of energy explicitly at any order
Atom kinetics：diffusion, reaction, catalysis
Linear Synchronous Transit (LST)
Quadratic Synchronous Transit (QST)
Nedged-Elastic Band (NEB)
(Henkelman, G.; Jonsson, H. "Improved
tangent estimate in the nudged elastic band
method for finding energy paths and saddle
points", J. Chem. Phys., 113, 9978 (2000).)
Surface, Interface
Surface energy
Approximation:
1. T = 0, E(AB) chose the crystal energy
2. Chemical potential: U(A)+U(B)= U(AB) = E(AB)
3. The range of U, U(A)<= E(A) (bulk) , U(B) <= E(B)
Excited states: band gap
 Excited state with same number electrons as
ground state
specific heat, line response, optical properties
 N -> N+1, or N -> N-1
photoemission, or inverse photoemission
Fundamental Gap
E gap min =min{(E[n+1]-E[n]) – (E[n]-E[n-1])}
Photoemssion Spectroscopy (PES)
Au (111)
Excited state: heat, conductivity…
• Keep electron number
Electron-Hole interaction (EHI)
E ex min < E gap min
LDA underestimate the gap
GW with (dot) and without
(dash line) EHI
Overview-I
Overview-II
Software
• Free
Siesta, Abinit, PWscf …
• Non-free
Gaussian, DMol3, CASTEP, VASP, Wien2K …