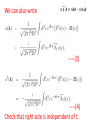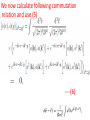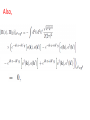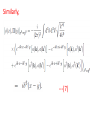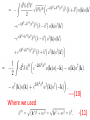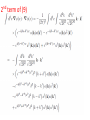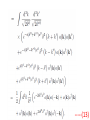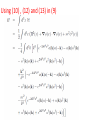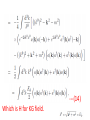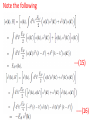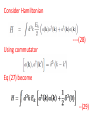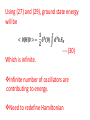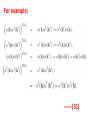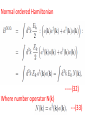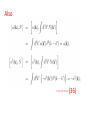* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Atomic theory wikipedia , lookup
Ferromagnetism wikipedia , lookup
Noether's theorem wikipedia , lookup
Coupled cluster wikipedia , lookup
Hydrogen atom wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Dirac bracket wikipedia , lookup
Hidden variable theory wikipedia , lookup
Bra–ket notation wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Quantum state wikipedia , lookup
Density matrix wikipedia , lookup
Zero-point energy wikipedia , lookup
Ising model wikipedia , lookup
Second quantization wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Topological quantum field theory wikipedia , lookup
Particle in a box wikipedia , lookup
Path integral formulation wikipedia , lookup
Wave–particle duality wikipedia , lookup
Casimir effect wikipedia , lookup
Renormalization group wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Coherent states wikipedia , lookup
Renormalization wikipedia , lookup
Quantum field theory wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
History of quantum field theory wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Chapter II Klein Gordan Field Lecture 2 Books Recommended: Lectures on Quantum Field Theory by Ashok Das A First Book of QFT by A Lahiri and P B Pal Creation and Annihilation operators Consider -----(1) Conjugate Momentum --(2) We can also write -----(3) ----(4) Check that right side is independent of t. We can write following commutation relations between the operators and , similar to harmonic oscillator: -------(5) We now calculate following commutation relation and use (5) ----(6) Also, Similarly, ---(7) We can also prove the commutators -----(8) By inserting the expressions of above Operators in terms of field operators i.e., Using(3) and (4). Perform above exercise. Now we calculate Hamiltonian using field expansions (1) and (2) ---(9) Where, 1st term of (9) ----(10) Where we used -(11) 2nd term of (9) -----(12) 3rd term of (9) -----(13) Using (10) , (12) and (13) in (9) ---(14) Which is H for KG field. Note the following ---(15) ----(16) Considering analogy between SHO and above discuss field theory, can be interpreted as annihilation operator and as creation operator. Positive energy component of the field Annihilate the quantum whereas the negative energy component create the quantum. This quantum is called a particle of positive energy. Normal Ordering We can defined the ground state ----(27) The state is normalized such that Consider Hamiltonian ----(28) Using commutator Eq (27) become --(29) Using (27) and (29), ground state energy will be ----(30) Which is infinite. Infinite number of oscillators are contributing to energy. Need to redefine Hamiltonian Energy differences are physical quantities not absolute energy. We can subtract the infinities and can Redefine the Hamiltonian. A consistent approach for this is known as normal ordering. When we have the expression involving the Product of annihilation and creation operators , we defined the normal ordered product by Moving all annihilation operators to the right Of all creation operators as if commutators Were zero For example: ------(31) Normal ordered Hamiltonian -----(32) Where number operator N(k) ---(33) Total number operator ---(34) We can find -------(35) Also ---------(36) Exercise: (i) Find the linear momentum operator for the Klein Gordon field using the Noehter Theorem i.e. find (ii) Use the field expansions in above and show That (iii) What will normal ordered form for P? Do we need Normal ordering for momentum? Note: For a gneral field as KG field is scalar i.e., And therefore, = 0 i.e., spin of particles Described by KG eq is zero.