Download Chapter 2 Part 1 ppt

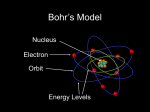
Chapter 2
Atomic Structure
• HW: 1, 3, 11, 13, 17, 20, 24, 25,
30, 32, 33, 39, 40
• The Periodic Table
• The Bohr Atom
• The Schrodinger Equation
• Orbitals
• Shielding
• Periodic Properties
of Atoms

Subatomic Particles
• 1885 - Balmer derived a formula to calculate
the energies of visible light emitted by the
hydrogen atom
 1
1 
E  R 2 - 2 
2
n 
E = h =
hc

= hc
n = integer, > 2
R = Rydberg constant for hydrogen
= 1.097 x 107 m–1
• General version of the
 1
1 
equation: E  R 2 - 2 
n h 
n l
n = principal quantum number, nl < nh
• Origin of energy unknown until Bohr’s atomic
theory (1913) derived same
 equation. 2 Z e
R = fundamental constant =
(4  ) h
Connection between experiment and theory
2
2 4
2
0
2
Bohr’s Atomic Theory
• Negatively charged electrons orbit the positively
charged nucleus
• When energy is absorbed, electrons move to
higher orbits
• When electrons move to lower
orbits, energy is emitted
• Equation predicted line spectra only
for single-electron atoms
• Adjustments were made to use
elliptical orbits to better fit data
• Ultimately failed - did not incorporate wave
properties of electrons. Still a useful theory.
Quantum Mechanics
• Particles as waves
h
=
(de Broglie)
m
• Uncertainty principle
(Heisenberg)
xpx 
h
4
Electrons - energy can be measured very accurately,
therefore cannot know position (x) with any certainty
• Probability of finding an electron at any position
(electron density = probability)
• Both Schrodinger and Heisenberg proposed ways to
treat electrons as waves, Schrodinger’s math was
easier
Wave Functions
• H= E  , where H operates on .
 - h2  2

2
2 
 2  2 + 2 + 2  + V(x, y, z)  (x, y, z) = E (x, y, z)
y
z 
 8 m  x

• Solutions to equation are wave functions, each
corresponding to an atomic orbital
• The conditions for a physically realistic solution:
-One value for electron density/point
-Continuous (does not change abruptly)
-Must approach zero as r approaches infinity
-Normalized (total probability = 1)
-Orthogonal
Atomic wave functions
• Solving equations requires 3 quantum numbers:
n, , m
• n - principal (size and energy)
 - angular momentum (shape, contributes to energy)
m - magnetic (orientation)
ms - spin (orientation of electron spin)
• Plot in 3-D space (spherical coordinates), need
3 variables: ,r,
• Break wavefunction into radial function (R), electron
density at distances from nucleus, and angular function
(, ), shape of orbital and orientation in space
•
R(r)·Y(, ) = R(r)· Y(x,y,z)
Angular Functions, Y(x,y,z)
• Table 2.3
• Determine how probability changes at a given
distance from the center of the atom (shape and
orientation in space)
• Look at real wave functions, in Cartesian
coordinates
• Where do orbital labels come from?
• Why are some regions shaded?
Radial Functions, R(r)
• Table 2.4
• 1s: n = 0,  = 0
3/2
Z  -
R = 2  e
a0 
( = Zr/a0 )
a0 = Bohr radius
(radius of first “orbit” for H atom)
2
h
=
= 52.9 pm 4 2 me2
 • Three ways to look at radial function:
R vs. r

2
R vs. r (probability)
4r2R2 vs. r (radial probability density)
Radial Probability Density
• 4r2R2: probability of finding electron at a given distance
from nucleus, summed over all angles
• Probability of finding the electron at a certain distance from
the nucleus is not equal to the probability of finding the
electron at a certain point at that distance from the
nucleus.
• There is a whole surface of a sphere on which we can find
the electron at that distance, r.
• 1s orbital: radial probability function has a maximum at
r = a0 (Bohr radius). This is the distance from the nucleus
where the electron in a 1s orbital is most likely found.
Homework Assignment
• Orbital plots (use Excel) for 1s, 2s, 2p, 3s, 3p,
3d, 4s, 4p, 4d, 4f orbitals (you have to find the
equations for the n=4 orbitals) (Orbitron!)
• Plot R, R2, and r2R2 (each as a function of )
Print all plots, showing function approaching
zero as  increases
• See Figure 2.7 for n = 1 to n = 3, R and r2R2
plots
Due date?