* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 2 Part 1 ppt
Renormalization wikipedia , lookup
Coupled cluster wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Particle in a box wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Density functional theory wikipedia , lookup
Molecular Hamiltonian wikipedia , lookup
Renormalization group wikipedia , lookup
Chemical bond wikipedia , lookup
Molecular orbital wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
Double-slit experiment wikipedia , lookup
Dirac equation wikipedia , lookup
Auger electron spectroscopy wikipedia , lookup
Wave function wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Wave–particle duality wikipedia , lookup
Electron scattering wikipedia , lookup
Tight binding wikipedia , lookup
Probability amplitude wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Hydrogen atom wikipedia , lookup
Atomic orbital wikipedia , lookup
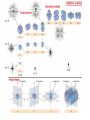
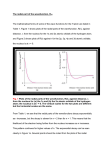
Chapter 2 Atomic Structure • HW: 1, 3, 11, 13, 17, 20, 24, 25, 30, 32, 33, 39, 40 • The Periodic Table • The Bohr Atom • The Schrodinger Equation • Orbitals • Shielding • Periodic Properties of Atoms Subatomic Particles • 1885 - Balmer derived a formula to calculate the energies of visible light emitted by the hydrogen atom 1 1 E R 2 - 2 2 n E = h = hc = hc n = integer, > 2 R = Rydberg constant for hydrogen = 1.097 x 107 m–1 • General version of the 1 1 equation: E R 2 - 2 n h n l n = principal quantum number, nl < nh • Origin of energy unknown until Bohr’s atomic theory (1913) derived same equation. 2 Z e R = fundamental constant = (4 ) h Connection between experiment and theory 2 2 4 2 0 2 Bohr’s Atomic Theory • Negatively charged electrons orbit the positively charged nucleus • When energy is absorbed, electrons move to higher orbits • When electrons move to lower orbits, energy is emitted • Equation predicted line spectra only for single-electron atoms • Adjustments were made to use elliptical orbits to better fit data • Ultimately failed - did not incorporate wave properties of electrons. Still a useful theory. Quantum Mechanics • Particles as waves h = (de Broglie) m • Uncertainty principle (Heisenberg) xpx h 4 Electrons - energy can be measured very accurately, therefore cannot know position (x) with any certainty • Probability of finding an electron at any position (electron density = probability) • Both Schrodinger and Heisenberg proposed ways to treat electrons as waves, Schrodinger’s math was easier Wave Functions • H= E , where H operates on . - h2 2 2 2 2 2 + 2 + 2 + V(x, y, z) (x, y, z) = E (x, y, z) y z 8 m x • Solutions to equation are wave functions, each corresponding to an atomic orbital • The conditions for a physically realistic solution: -One value for electron density/point -Continuous (does not change abruptly) -Must approach zero as r approaches infinity -Normalized (total probability = 1) -Orthogonal Atomic wave functions • Solving equations requires 3 quantum numbers: n, , m • n - principal (size and energy) - angular momentum (shape, contributes to energy) m - magnetic (orientation) ms - spin (orientation of electron spin) • Plot in 3-D space (spherical coordinates), need 3 variables: ,r, • Break wavefunction into radial function (R), electron density at distances from nucleus, and angular function (, ), shape of orbital and orientation in space • R(r)·Y(, ) = R(r)· Y(x,y,z) Angular Functions, Y(x,y,z) • Table 2.3 • Determine how probability changes at a given distance from the center of the atom (shape and orientation in space) • Look at real wave functions, in Cartesian coordinates • Where do orbital labels come from? • Why are some regions shaded? Radial Functions, R(r) • Table 2.4 • 1s: n = 0, = 0 3/2 Z - R = 2 e a0 ( = Zr/a0 ) a0 = Bohr radius (radius of first “orbit” for H atom) 2 h = = 52.9 pm 4 2 me2 • Three ways to look at radial function: R vs. r 2 R vs. r (probability) 4r2R2 vs. r (radial probability density) Radial Probability Density • 4r2R2: probability of finding electron at a given distance from nucleus, summed over all angles • Probability of finding the electron at a certain distance from the nucleus is not equal to the probability of finding the electron at a certain point at that distance from the nucleus. • There is a whole surface of a sphere on which we can find the electron at that distance, r. • 1s orbital: radial probability function has a maximum at r = a0 (Bohr radius). This is the distance from the nucleus where the electron in a 1s orbital is most likely found. Homework Assignment • Orbital plots (use Excel) for 1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f orbitals (you have to find the equations for the n=4 orbitals) (Orbitron!) • Plot R, R2, and r2R2 (each as a function of ) Print all plots, showing function approaching zero as increases • See Figure 2.7 for n = 1 to n = 3, R and r2R2 plots Due date?