Introduction in energy systems - Faculty of Mechanical Engineering
... required to make room for it by displacing its environment and establishing its volume and pressure. Enthalpy is defined as a state function that depends only on the prevailing equilibrium state identified by the variables internal energy, pressure, and volume. It is an extensive quantity. The entha ...
... required to make room for it by displacing its environment and establishing its volume and pressure. Enthalpy is defined as a state function that depends only on the prevailing equilibrium state identified by the variables internal energy, pressure, and volume. It is an extensive quantity. The entha ...
Bagian 2 termodinamika
... hot body heat cannot be transformed completely into mechanical work it is impossible to construct an operational perpetual motion machine ...
... hot body heat cannot be transformed completely into mechanical work it is impossible to construct an operational perpetual motion machine ...
Thermodynamics for Systems Biology
... approached to arbitrary accuracy, at least as gedanken processes. In such processes we define a conserved quantity, the entropy, again by how it changes. For one system, the differential change in its entropy, S, is defined in terms of the differential amount of heat dQrev entering or leaving the s ...
... approached to arbitrary accuracy, at least as gedanken processes. In such processes we define a conserved quantity, the entropy, again by how it changes. For one system, the differential change in its entropy, S, is defined in terms of the differential amount of heat dQrev entering or leaving the s ...
Title - ALevelChemistryRossett
... Note 2: The term T∆S is temperature dependent meaning that some reactions may be feasible at one temperature but not at another. Note 3: A reaction with ∆G negative means it can go. It does not necessarily mean that it will go. There is the kinetics of a reaction to take into account as well as the ...
... Note 2: The term T∆S is temperature dependent meaning that some reactions may be feasible at one temperature but not at another. Note 3: A reaction with ∆G negative means it can go. It does not necessarily mean that it will go. There is the kinetics of a reaction to take into account as well as the ...
Thermodynamic Characteristics of Solid
... In conclusion, it is worth noting that the essential feature of the considered phenomenon has been discovered. It is about the quantum nature and it appears that the reality, as considered in the macroscopic scale, also possesses quantum energetic nature. Thus not only the microscopic world is quant ...
... In conclusion, it is worth noting that the essential feature of the considered phenomenon has been discovered. It is about the quantum nature and it appears that the reality, as considered in the macroscopic scale, also possesses quantum energetic nature. Thus not only the microscopic world is quant ...
File
... (e) Flow of water from a hill to the ground. (f) Mixing of gases. In all the above cases, the system reaches a state of greater disorder. Eventhough the energy of the system increases (endothermic) during the above changes the processes are spontaneous because they are accompanied with increase in e ...
... (e) Flow of water from a hill to the ground. (f) Mixing of gases. In all the above cases, the system reaches a state of greater disorder. Eventhough the energy of the system increases (endothermic) during the above changes the processes are spontaneous because they are accompanied with increase in e ...
Chapter 4 Entropy and second law of thermodynamics
... multiplicity of = that correspond to the . a macrostate macrostate 2. The entropy can be defined in terms of the multiplicity as S ≡ kB ln (multiplicity) . We shall see in statistical mechanics that this definition is equivalent to the phenomenological concept we have learnt previously in this s ...
... multiplicity of = that correspond to the . a macrostate macrostate 2. The entropy can be defined in terms of the multiplicity as S ≡ kB ln (multiplicity) . We shall see in statistical mechanics that this definition is equivalent to the phenomenological concept we have learnt previously in this s ...
Thermodynamics of ideal gases
... slow quasistatic processes, consisting of infinitely many infinitesimal reversible steps. Essentially all real-world processes are irreversible to some degree. Example D.3.1 (Joule’s expansion experiment): An isolated box of volume V contains an ideal gas in a walled-off compartment of volume V0 . W ...
... slow quasistatic processes, consisting of infinitely many infinitesimal reversible steps. Essentially all real-world processes are irreversible to some degree. Example D.3.1 (Joule’s expansion experiment): An isolated box of volume V contains an ideal gas in a walled-off compartment of volume V0 . W ...
Lecture 4
... Let us consider the relation (4.46) If we regard =1/kT as a complex variable, then the partition function Z() is just Laplace transform of the density of states g(E). ...
... Let us consider the relation (4.46) If we regard =1/kT as a complex variable, then the partition function Z() is just Laplace transform of the density of states g(E). ...
0.1 Minimum Principles and Thermodynamic Potentials
... The minimum principle for G then states that for all states at a fixed T and P , the equilibrium state is that for which G is a minimum. The proof is very similar to that for A: the second law states that ∆Q ≤ T ∆S or 0 ≥ T ∆S + ∆U + P ∆V , if P is held fixed. But dG = dU − T dS + P dV , so dG ≤ 0 i ...
... The minimum principle for G then states that for all states at a fixed T and P , the equilibrium state is that for which G is a minimum. The proof is very similar to that for A: the second law states that ∆Q ≤ T ∆S or 0 ≥ T ∆S + ∆U + P ∆V , if P is held fixed. But dG = dU − T dS + P dV , so dG ≤ 0 i ...
Chapter 15 Notes - Valdosta State University
... wall. One that does not is said to be adiabatic. The state of a system is described by specifying factors that affect the internal energy of the system. In the case of a gas this would be temperature, pressure, volume, and mass. There are three laws of thermodynamics. The first one is called the Zer ...
... wall. One that does not is said to be adiabatic. The state of a system is described by specifying factors that affect the internal energy of the system. In the case of a gas this would be temperature, pressure, volume, and mass. There are three laws of thermodynamics. The first one is called the Zer ...
The Thermodynamic Potentials
... the laboratory. The experimenter frequently finds that the intensive parameters are the more easily measured and controlled and therefore is likely to think of the intensive parameters as operationally independent variables and of the extensive parameters as operationally derived quantities. The ext ...
... the laboratory. The experimenter frequently finds that the intensive parameters are the more easily measured and controlled and therefore is likely to think of the intensive parameters as operationally independent variables and of the extensive parameters as operationally derived quantities. The ext ...
Thermochemistry
... We can define a new state variable (one where the path to its current state does not affect its value) called enthalpy: ...
... We can define a new state variable (one where the path to its current state does not affect its value) called enthalpy: ...
Econophysics: Entropy and its discontents?
... Econophysics: Entropy and its discontents? For over fifty years, neoclassical and biophysical economists have been divided in their views regarding the extent to which the second law of thermodynamics- the “entropy law”- is applicable to the field of economics and sustainable growth. According to ec ...
... Econophysics: Entropy and its discontents? For over fifty years, neoclassical and biophysical economists have been divided in their views regarding the extent to which the second law of thermodynamics- the “entropy law”- is applicable to the field of economics and sustainable growth. According to ec ...
Fundamentals of chemical thermodynamics and bioenergetics
... (In thermodynamics, such a process is called an adiabatic process.) Thus, we write ΔU = Q + W = W. Because the system does work on the surroundings, W is a negative quantity, and there is a decrease in the system’s energy. The change in energy ΔU is given by ΔU = CΔT, where C is the proportionality ...
... (In thermodynamics, such a process is called an adiabatic process.) Thus, we write ΔU = Q + W = W. Because the system does work on the surroundings, W is a negative quantity, and there is a decrease in the system’s energy. The change in energy ΔU is given by ΔU = CΔT, where C is the proportionality ...
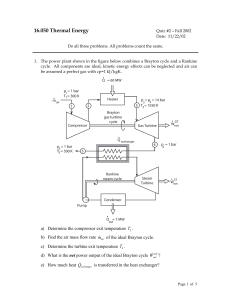
16.050 Thermal Energy
... g) What is the overall thermal efficiency of the combined cycle? 2. The sketch below shows a perfectly insulated container with two compartments separated by a non-adiabatic, frictionless piston. Both compartments are at the same pressure (pA = pB) and contain an equal amount of the same gas (mA = m ...
... g) What is the overall thermal efficiency of the combined cycle? 2. The sketch below shows a perfectly insulated container with two compartments separated by a non-adiabatic, frictionless piston. Both compartments are at the same pressure (pA = pB) and contain an equal amount of the same gas (mA = m ...
Some useful Statistical Thermodynamics 1 Introduction
... The second law states that the number of accessible micro-states of an isolated system, Ω, never decreases. If we consider subsystem A to contain and ideal atomic gas, then the number of accessible micro-states of A is simply the number of places in space that may be occupied by the gas atoms. Thus, ...
... The second law states that the number of accessible micro-states of an isolated system, Ω, never decreases. If we consider subsystem A to contain and ideal atomic gas, then the number of accessible micro-states of A is simply the number of places in space that may be occupied by the gas atoms. Thus, ...
Entropy in thermodynamics and information theory
There are close parallels between the mathematical expressions for the thermodynamic entropy, usually denoted by S, of a physical system in the statistical thermodynamics established by Ludwig Boltzmann and J. Willard Gibbs in the 1870s, and the information-theoretic entropy, usually expressed as H, of Claude Shannon and Ralph Hartley developed in the 1940s. Shannon, although not initially aware of this similarity, commented on it upon publicizing information theory in A Mathematical Theory of Communication.This article explores what links there are between the two concepts, and how far they can be regarded as connected.