Download Lesson 2

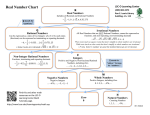
Lesson 2.7: Square Roots and Real Numbers.
Learning objectives for this lesson – By the end of this lesson, you will be able to:

Find square roots.

Approximate square roots.

Identify irrational numbers.

Classify real numbers.

Graph and order real numbers.
California State Standards Addressed: Algebra I (1.1, 2.0, 24.0, 25.1, 25.2)
2.7.1. Find square roots.
The square root of a number is a number which, when multiplied by itself gives the original number. In
algebraic terms, the square root of x is a number, b, such that b2 = x.
Note: There are two possibilities for a numerical value for b. The positive number that satisfies the
equation b2 = x is called the principal square root. Since (–b)·(–b) = + b2 = x, –b is also a valid solution.
The square root of a number, x, is written as
root of 4,
x or sometimes as 2 x . For example, 22 = 4, so the square
4  2 . It is common to refer to square roots as radicals:
4 would therefore be read as “radical 4”
7 would be read as “radical 7”
x would be read as “radical x”
Some numbers, like 4, have integer square roots. Numbers with integer square roots are called perfect
squares. The first five perfect squares (1, 4, 9, 16, 25) are shown below.
1×1
2×2
3×3
4×4
5×5
You can determine whether a number is a perfect square by looking at its prime factors. If every number in
the factor tree appears an even number of times, the number is a perfect square. Further, to find the square
root of that number, simply take one of each pair of factors, and multiply together:
Example 1
Find the principal square root of each of these perfect squares:
a) 121
a) 121 = 11 × 11
b) 225
Solution:
b) 225 = (5 × 5) × (3 × 3)
c) 324
d) 576
121  11
Solution:
c) 324 = (2 × 2) × (3 × 3) × (3 × 3)
225  5  3  15
Solution:
d) 576 = (2 × 2) × (2 × 2) × (2 × 2) × (3 × 3)
324  2  3  3  18
Solution:
576  2  2  2  3  24
When we have an odd number of prime factors we leave any unpaired factors under a radical sign. Any
answer that contains both whole numbers and irreducible radicals should be written A b .
Example 2
Find the principal square root of the following:
a) 8
b) 48
c) 75
d) 216
a) 8 = (2 × 2) × 2
Solution:
8  2 2  2 2
b) 48 = (2 × 2) × (2 × 2) × 3
Solution:
48  2  2  3  4 3
c) 75 = (5 × 5) × 3
Solution:
75  5  3  5 3
d) 216 = (2 × 2) × 2 × (3 × 3) × 3
Solution:
216  2  2  3  3  6 2 3  6 6
Note that in the last example we collected the whole numbers and multiplied them first, then we collect
unpaired primes under a single radical symbol. The four rules that govern how we treat radicals are:
a  b  ab
A a  B b  AB ab
a b
A a B b 
a
b
A a
B b
Example 3
Simplify the following square root problems:
a)
a)
8 2
b) 3 4  4 3
c)
8  2  16
Solution:
12  3 
12
 4
3
d) 12 10  6 5 
d) 12 10  6 5
8 2= 4
Solution: 3 4  4 3  24 3
b) 3 4  4 3  12 12  12 (2  2)  3  12  2 3
c)
12  3
Solution:
12 10
6 5
12  3 = 2
Solution: 12 10  6 5  2 2
2.7.2. Approximate square roots.
When we have perfect squares we can write an exact numerical solution for the principal square root. When
we have 1 or more unpaired primes in the factor tree of a number, however, we do not get integer values for
the square root and we have seen that we leave a radical in the answer. Terms like
2 , 3 and
7 (square
roots of prime numbers) cannot be written as rational numbers. That is to say, they cannot be expressed as
the ratio of two integers. We call them irrational numbers. In decimal form, they have an unending,
seemingly random, string of numbers after the decimal point.
To find approximate values for square roots, we use the
or
x
button on a calculator. When the
number we are finding the square root of is a perfect square, or the square of a rational number, we will get
an exact answer. When the answer involves 1 or more unpaired primes, the decimals will appear random
and we will have an irrational number as our answer. We call this an approximate answer – even though
we may have an answer to 8 or 9 decimal places, it still represents an approximation of the real answer
which has an infinite number of non-repeating decimals.
Example 4
Use a calculator to find the following square roots. Round your answer to 3 decimal places.
a)
99
b)
5
c)
0.5
a) The calculator returns 9.949874371
Solution:
99  9.950
b) The calculator returns 2.236067977
Solution:
5  2.236
c) The calculator returns 0.7071067812
Solution:
0.5  0.707
d) The calculator returns 1.322875656
Solution:
1.75  1.323
d) 1.75
2.7.3. Identify irrational numbers.
Any square root that cannot be simplified to a form without a radical is irrational, but not all square roots
are irrational. For example
49 reduces to 7 and so
49 is rational, but
50 cannot be reduced further
than 25  2  5 2 .The fact that we cannot remove the factor of radical 2 makes
50 irrational.
Example 5
Identify which of the following are rational numbers and which are irrational numbers.
a) 23.7
c) π
b) 2.8956
d)
6
e) 3.27
7
. This is clearly a rational number.
10
a)
23 .7  23
b)
2.8956  2
c)
π = 3.141592654… The decimals appear random, and there is no indication that they are likely to end
8956
. Again, this is a rational number.
10000
any time soon – this is an irrational number.
d)
6 = 2.44949489743… Again the decimals appear to be random. We also know that
Square roots of primes are irrational.
e)
6  2 3 .
6 is an irrational number.
3.27 =3.2727272727… Although these decimals are recurring they are certainly not unpredictable.
This is a rational number (in actual fact, 3.27 
36
)
11
2.7.4. Classify real numbers.
We can now see how real numbers fall into one of several categories:
Real Numbers
Rational Numbers
Integers
Irrational Numbers
Fractions
If a real number can be expressed as a rational number it falls into 1 of two categories – if the denominator
of its simplest form is 1, then it is an integer. If not, it is a fraction (this term is used here to also include
decimals, as 3.27 = 3
27
. If the number cannot be expressed as the ratio of 2 integers, it is irrational.
100
Example 6
Classify the following real numbers:
a) 0
b) -1
c)

3
d)
2
3
e)
36
9
a) Solution: 0 is an integer.
b) Solution: -1 is an integer.
c) Although


is written as a fraction, the numerator (π) is irrational. Solution:
is an irrational
3
3
number.
d)
2
2
cannot be simplified to remove the radical. Solution:
is an irrational number.
3
3
e)
36
can be simplified to
9
36 6 2
  Solution:
3
9 3
36
is a rational number.
9
02.7.5. Graph and order real numbers.
We have already talked about plotting integers on the number line. It gives a visual representation of which
number is bigger, smaller, etc. It would therefore be helpful to plot non-integer rational numbers (fractions)
on the number line also. There are 2 ways to graph rational numbers on the number line: you can convert
them to a mixed number (graphing is one of the few instances in algebra when mixed numbers are
preferred to improper fractions), or you can convert do decimal form.
Example 7
Plot the following rational numbers on the number line.
a)
2
3
b) 
3
7
c)
17
3
d)
57
16
If we divide the intervals on the number line into the number on the denominator, we can look at the
fraction’s numerator to determine how many of these sub-intervals we need to include
a)
2
falls between 0 and 1. We divide the interval into 3, and include 2 sub-intervals:
3
-2
b) 
-1
0
2
3
1
2
3
falls between 0 and -1. We divide the interval into 7, and move left from 0 by 3 sub-intervals:
7
-2
c)
-1

3
7
1
0
17
2
as a mixed number is 3 and falls between 3 and 4. We divide the interval into 5, and move over 2:
5
5
17
1
0
d)
2
3
4
5
5
57
9
as a mixed number is 3
and falls between 3 and 4. We need to make 16 sub-divisions this time:
16
16
1
0
2
57
16
3
4
Example 8
Plot the following numbers, in the correct order, on a number line:
a) 
b)
22
7
c) 3.14
d)
10
We will use a calculator to find decimal expansions for each of these, and a number line divided with 1000
sub-divisions. When we have 2 extremely close numbers, we will ensure that we place them in the correct
order by looking at the expansion to the 3rd decimal place and writing as a fraction of 1000.
142
1000
a)
  3.14159 ...  3
b)
22
143
 3.14288 ...  3
7
1000
c)
3.14  3
d)
140
1000
10  3.16227 ...  3
162
1000
Solution:
c ab
3.130
3.140
d
3.150
3.160
3.170
Homework Problems
1.
2.
3.
Find the following square roots exactly, giving your answer in the simplest form:
a)
25
b)
24
c)
20
d)
200
e)
2000
f)
1
4
g)
9
4
h)
0.16
i)
0.1
j)
0.01
Use a calculator to find the following square roots. Round to 2 decimal places:
a)
13
b)
99
c)
123
d)
2
e)
2000
f)
0.25
g)
1.35
h)
0.37
i)
0.7
j)
0.01
Classify the following numbers as integer, rational number or irrational number:
a)
4.
c)
d)
20
e)
25
100
Place the following numbers in numerical order, lowest to highest.
6 61
;
;
2
50
5.
b) 1.35
0.25
1.6 ;
16
13
Write the following numbers on the number line as proper fractions.
1
0
c
b
a
2
d
3
4
Answers:
1. a) 5; b) 2 6 ; c) 2 5 ; d) 10 2 ; e) 20 5 ; f)
1
3
; g) ; h) 0.4; i)
2
2
1
10
or
10
; j) 0.1
10
2. a) 3.61; b) 1.16; c) 9.95; d) 11.09; e) 44.72; f) 0.5; g) 1.16; h) 0.61; i) 0.84; j) 0.1
3. a) rational; b) irrational; c) irrational; d) integer; e) integer
4. a)
61
;
50
6 16
;
;
2
13
5. a)
2
9
9
34
; b) ; c) ; d)
3
5
4
9
1.6