Download LECTURE 22 THE STRONG COUPLING CONSTANT, QUARK-GLUON PLASMA (QGP)

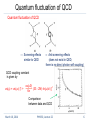
LECTURE 22
THE STRONG COUPLING CONSTANT,
QUARK-GLUON PLASMA (QGP)
PHY492 Nuclear and Elementary Particle Physics
Questions from Last Lecture
What are 8 color states for gluons ? rb rg bg gr br gb ( rr − gg ) / √2 ( rr + gg − 2 bb ) / √6 ( rr + gg + bb ) / √3 How one can explain the finite range of the strong
interaction with the Coulomb-like potential ? V(r) = - a(hc) + br
r hc March 10, 2014 PHY492, Lecture 22 2 One-gluon exchange potential
The level structure of charmonium ( cc ) and bottomium ( bb ) is
also similar to that seen in the positronium There should be a major contribution from
a single-particle exchange with a “Coulomb-like” form.
( one gluon exchange )
a(hc)
V(r) = - r a is proportional to the strong interaction analogue
of the fine structure constant α in QED To account for the quark confinement, we need to add a confining potential V(r) = - a(hc) + br
r hc Mass of the cc and bb systems can be explained
with the same values a ≈ 0.48 and b ≈ 0.18 GeV2 (flavour independence)
March 10, 2014 PHY492, Lecture 22 3 Strong coupling constant
Asymptotic freedom
: the strong interaction gets weaker at short distances
One has to regard the strong coupling as αs decreasing with
increasing momentum transfer |q| which is given by O(h/r).
strength of the interaction depends on
µ2 = | q2 – Eq2/c2 |
(Lorentz invariant)
coupling constant ( running coupling constant ) is given by
αs =
6π
(33 - 2Nf) ln(µ/Λ) for µ2 >> 1 (GeV/c)2, Nf : number of quark flavours with 4(mqc)2 < µ2,
Λ = 0.2 (0.1) GeV/c obtained from many measurements
forces that increase with increasing separation
spring or elastic string → at some limits, the string breaks
strong force → create q q pairs (fragmentation) March 10, 2014 PHY492, Lecture 22 4 Quantum fluctuation of QED
Quantum fluctuation of QED
: single electrons are considered to emit and re-absorve photons
continually ( case (a) ), in addition to the usual case (b) for the
one-photon exchange
More complicated diagrams can be considered , if we include
vacuum polarization effects for a ‘sea’ of virtual electrons and positrons,
which produces a shielding effect
QED coupling constant
thus increases with µ, slightly
2
αem = α[ 1 - 3π
α ln(
March 10, 2014 PHY492, Lecture 22 µ
-1 )]
µ0
5 Quantum fluctuation of QCD
Quantum fluctuation of QCD
→ Screening effects
similar to QED → Anti-screening effects
(does not exist in QED,
there is no direct photon self-coupling) QCD coupling constant
is given by αs(µ) = αs(µ0) [1 +
αs(µ0)
-1 6π
(33 - 2Nf) ln(µ/µ0) ]
Comparison
between data and QCD
March 10, 2014 PHY492, Lecture 22 6 Example, calculation of αs
Comparison
between data and QCD
March 10, 2014 PHY492, Lecture 22 7 Phase transition of matter
•  Solid –  Definite shape –  Definite volume •  Liquid –  No definite shape –  Definite volume •  Gas –  No definite shape –  No definite volume •  Plasma Phase transition of nuclei ?
March 10, 2014 PHY492, Lecture 22 8 Quark gluon plasma
In QCD, quarks and gluons are confined within hadrons
at normal energy-densities.
At extremely high energy-densities, QCD predicts that
the quarks and gluons would become de-confined,
producing Quark-Gluon plasma (QGP)
(a)  Two heavy ion collision
(b)  Interact via the colour field
(c) Very high energies causes
the quarks and gluons
deconfined (QGP)
(d)  As the plasma cools,
hadrons condense and emitted March 10, 2014 PHY492, Lecture 22 9