* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Genetic Algorithms: Genetic Algorithm Applications to Actuarial Problems ARC 2012
Vectors in gene therapy wikipedia , lookup
Polymorphism (biology) wikipedia , lookup
Genetically modified food wikipedia , lookup
Gene therapy wikipedia , lookup
Genome evolution wikipedia , lookup
Artificial gene synthesis wikipedia , lookup
Koinophilia wikipedia , lookup
Quantitative trait locus wikipedia , lookup
Site-specific recombinase technology wikipedia , lookup
Biology and consumer behaviour wikipedia , lookup
Genetic code wikipedia , lookup
Pharmacogenomics wikipedia , lookup
Genetic drift wikipedia , lookup
Medical genetics wikipedia , lookup
Behavioural genetics wikipedia , lookup
Heritability of IQ wikipedia , lookup
Gene expression programming wikipedia , lookup
Designer baby wikipedia , lookup
Population genetics wikipedia , lookup
Human genetic variation wikipedia , lookup
History of genetic engineering wikipedia , lookup
Genetic testing wikipedia , lookup
Genetic engineering wikipedia , lookup
Public health genomics wikipedia , lookup
Genetic engineering in science fiction wikipedia , lookup
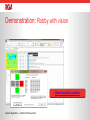
ARC 2012 Genetic Algorithms: Genetic Algorithm Applications to Actuarial Problems Dave Snell, ASA, MAAA, CLU, ChFC, FLMI, MCP, ARA, ACS Technology Evangelist, Vice Chairman’s Office RGA Reinsurance Company Genetic Algorithms – 4-AUG-2012 Dave Snell SOCIETY OF ACTUARIES Why do we call these Genetic Algorithms? They mimic our current knowledge of genetics. We have trillions of cells. DNA represents a blueprint for a cell. It is used to generate copies. The actual process involves proteins and lots of other biological terms … Genetic Algorithms – 4-AUG-2012 Dave Snell Mitosis – exact copies Meiosis – copy portions from two parents Mutation – inexact copy – rarely lives Over time - a long time - we evolve … taller, less hairy, and more adept at making tools. Genetic Algorithms – 4-AUG-2012 Dave Snell Very basic genetics § Humans have about 25,000 genes made from A-T and C-G pairs § DNA strand – double helix of two strands – each about 1.8 meters § In meiosis, the strand separates into 46 chromosomes (in 23 pairs) § Alleles (forms of a gene) help determine physical or behavioral traits Genetic Algorithms – 4-AUG-2012 Dave Snell Does the size of a Genome determine species dominance? NO! – It’s all in how you use it! § Human 3,200,000,000 (3.2Gb) § Lungfish130,000,000,000 (130Gb) § "Amoeba" 670,000,000,000 (670Gb) Genetic Algorithms – 4-AUG-2012 Dave Snell Where is the Research being done on Genomes? All over the world; but especially … National Institutes of Health (NIH) “This is why I go to work!” RMS – rhabdomyosarcoma -Frederick S. Huang, MD The Genome Institute at Washington University Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms Meet Amoeba Robby Robby is only able to do 7 actions: 0-Move North 1 square 1-Move South 1 square 2-Move West1 square 3-Move East 1 square 4-Stay put 5-Pick up a can 6-Make random move (from 0-5) Our first Robby is blind! Story of Robby simplified from Complexity: A Guided Tour by Melanie Mitchell, Ph.D. Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (cont.) § Robby actions can be represented by a strategy 0- north 1 string, like ‘35265’ 1- south 1 (move East, pickup, move South, random, pickup) 2- west 1 3- east 1 4-Stay put 5-Pick up 6-random § In 100 steps, what strategy would you use to pick up as many randomly placed cans as possible? You get 10 points for each can. Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (cont.) § Robby actions can be represented by a strategy 0- north 1 string, like ‘35265’ 1- south 1 (move East, pickup, move South, random, pickup) 2- west 1 § In 100 steps, what strategy would you use to pick up as many randomly placed cans as possible? You get 10 points for each can. 3- east 1 4-Stay put 5-Pick up 6-random • Oh yeah! … you lose 5 points every time you hit a wall. Genetic Algorithms – 4-AUG-2012 Dave Snell Try all possibilities? 7^100 > 10^84 so trying all possibilities might take too long … compare to around 10^17 seconds since Big Bang billions of years ago Genetic Algorithms – 4-AUG-2012 Dave Snell Hill Climbing … works really well when there is only one hill Mount Everest? Our family in Tibet Yak, yak, yak Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (a simplistic recipe) 1. Randomly assign the gene string for 100 robots. 2. Run 100 tests with cans scattered randomly. 3. Score each robot and eliminate losers (survival of the fittest). 4. Assign mating privileges to survivors per test scores. In a kangaroo mob, only the highest ranking male gets mating privileges Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (simplistic recipe continued.) 5. Pick parents, and pair them off to produce the next generation Parent M (52.80 points): 54335351253404 315142153601520652551511513145155663 Parent F (45.60 points) :54335351525534 633242153604216362551511503145155625 arbitrary (pseudo-random) split point Child A: 54335351253404 633242153604216362551511503145155625 genes from parent M genes from parent F Child B: 54335351525534 315142153601520652551511513145155663 Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (simplistic recipe wrap-up.) 1. 2. 3. 4. 5. 6. 7. Randomly assign the initial gene strings. Run tests. Score each robot and eliminate losers. Assign mating privileges to highest scorers. Pick parents, and produce next generation. Randomly mutate a few genes (actions). Repeat for 100 (or 1,000 or 10,000) generations. Genetic Algorithms – 4-AUG-2012 Dave Snell Demonstration: Blind Robby Watch evolution in action Genetic Algorithms – 4-AUG-2012 Dave Snell Genetic Algorithms (How twins are made) Genetic Algorithms – 4-AUG-2012 Dave Snell Let’s give Robby a sense of Vision Robby can see five squares: the current square. the square immediately to the East the square immediately to the South the square immediately to the West the square immediately to the North Assume each of these five squares can have three different states: 0 = Empty; 1= Contains a can; 2 = Wall The total number of visual cases is (3 states/cell) ^(5 visible cells) = 243 Genetic Algorithms – 4-AUG-2012 Dave Snell Robby with Vision (continued) Let’s number these 243 cases from 0 to 242 3^4 North 3^3 West 3^2 South 3^1 East 3^0 Current Case 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 2 0 0 1 2 3 2 2 2 2 2 2 2 2 1 2 241 242 … Case Robby is in a wall (not possible) other impossible cases Action 0 MoveNorth 1 PickUpCan 2 MoveSouth 3 MoveNorth 241 MoveEast 242 MoveWest It doesn’t matter that some of the cases are not physically possible. Our case table mathematics is not limited by the possible! Generation 1 will have a randomly generated column of actions. Future generations inherit actions from parents. Genetic Algorithms – 4-AUG-2012 Dave Snell Robby with Vision (continued) ‘ Suppose we want the action for this situation: Robby sees a wall to the East and cans to the North and South. Genetic Algorithms – 4-AUG-2012 Dave Snell Robby with Vision (continued) This would correspond to case number 96 in the virtual case table, calculated as follows: 0*3^0 (current) + 2*3^1 (East) + 1*3^2 (South) + 0*3^3 (West) + 1*3^4 (North) = 0+6+9+0+81 = 96 CASE TABLE Case Number Current East 0 0 1 0 … 96 0 … 242 2 South West North 0 0 0 0 0 0 0 1 2 1 0 1 2 2 2 2 Genetic Algorithms – 4-AUG-2012 Dave Snell Action MoveEast MoveEast … MoveNorth … PickUpCan For this particular ‘gene string’, case number 96 results in action MoveNorth. Note: The actions for any particular gene string do not have to make sense! Only the better ones survive and propagate. Demonstration: Robby with vision Watch evolution in action Genetic Algorithms – 4-AUG-2012 Dave Snell Mitosis & Meiosis Our Elites correspond to Mitosis Genetic Algorithms – 4-AUG-2012 Dave Snell The rest of the new generation are analogous to Meiosis Meiosis in action - Genetics 0.001 Parent 'M' Gene Parent 'F' Child1 Child2 Child3 Child4 1 Dad Mom Dad Mom Dad's Dad Mom's Dad Dad's Mom Mom's Mom Dad's Dad Mom's Mom Dad's Mom Mom's Dad 2 Dad Mom Dad Mom Dad's Mom Mom's Mom Dad's Mom Mom's Dad Dad's Mom Mom's Mom Dad's Mom Mom's Dad 3 Dad Mom Dad Mom Dad's Dad Mom's Mom Dad's Mom Mom's Mom Dad's Mom Mom's Mom Dad's Mom Mom's Dad 4 Dad Mom Dad Mom Dad's Dad Mom's Dad Dad's Dad Mom's Mom Dad's Mom Mom's Mom Dad's Mom Mom's Mom … 5,000 5001 … Note that each child gene is from two of the four grandparents: one on Mom’s side, one on Dad’s side (excluding mutations) Dad Mom Dad Mom Dad's Mom Mom's Mom Dad's Dad Mom's Mom Dad's Dad Mom's Mom Dad's Mom Mom's Mom Dad Mom Dad Mom Dad's Mom Mom's Dad Dad's Mom Mom's Dad Dad's Mom Mom's Dad Dad's Dad Mom's Dad set of genes from Parent genes prior to meiosis – eachDad person gets one set from Dad and another set from Mom Genetic Algorithms – 4-AUG-2012 Dave Snell set of genes from Mom Genetic Algorithms are not limited to two parents (or even four grandparents) Your ‘genes’ can have vastly different characteristics and components. A ‘child’ can have genes drawn from several different parents. Genetic Algorithms – 4-AUG-2012 Dave Snell That was fun! … but let’s see a Health Insurance application of Genetic Algorithms. Brian Grossmiller’s application: How to find a more cost effective set of health providers and still have adequate coverage. Genetic Algorithms – 4-AUG-2012 Dave Snell Demonstration: Health Provider Network Gene$c Algorithms – 4-‐AUG-‐2012 Dave Snell But does it work? § Overall Network Relativity: 1.00 § Actuaries (using standard optimization techniques): 0.72 § Genetic Algorithm: 0.54 (lower number is better … a lot lower is a lot better) Genetic Algorithms – 4-AUG-2012 Dave Snell Basics to take home with you § Keep problem manageable § Define objective § Robby - clean world § Provider Network - lower health costs and adequate coverage § Define universe for the actors § Robby - 10x10 grid littered with soda cans § Provider Network - all available providers, their specialties, their relative costs § Define actions – how actors change the universe § Blind Robby – deterministic gene string with 7 possible actions for each gene § Robby with vision – adapts to environment and chooses actions (from 7) § Provider network – deterministic gene string, simple IN or OUT of network § Create evaluation/ranking scheme (points for cans, or relative cost) § Make a reproductive model § Blind Robby and Robby with Vision – 2 parents and a crossover point § Provider network - N parents and pseudo-random selection gene-by-gene § Validate (save entire gene string for best set and verify it works) Genetic Algorithms – 4-AUG-2012 Dave Snell Wrap-up, and Feedback Most actuarial presentations are like mathematics, 1/2 the people can’t understand them … and the other 2/3 don’t care about them Good tools and Fun? … Bonus video 1 - Robby … or did we waste your time? Bonus video 2- EC gain Bonus video 3 – EC strategy Let’s Talk! Genetic Algorithms – 4-AUG-2012 Dave Snell SOCIETY OF ACTUARIES ARC 2012 Genetic Algorithms: Genetic Algorithm Applications to Actuarial Problems Dave Snell, ASA, MAAA, CLU, ChFC, FLMI, MCP, ARA, ACS Technology Evangelist, Vice Chairman’s Office RGA Reinsurance Company Genetic Algorithms – 4-AUG-2012 Dave Snell SOCIETY OF ACTUARIES