Download Electric Field

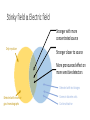
Electric Field Summary
The stinky field
If you have spent time around
infants, you are likely familiar with
the STINKY FIELD:
 Stronger effect when you’re
closer
 Stronger effect with more
concentrated source
 Stronger effect on better
detectors
Stinky field  Electric field
Stronger with more
concentrated source
Only repulsive
Stronger closer to source
More pronounced effect on
more sensitive detectors
Detected with test charges
Detected with noses or
gas chromatographs
Comes in discrete units
Can be attractive
Electric Field
𝐹
𝐸≝
𝑞
The strength of the electric field 𝐸 is defined as the force
exerted on a miniscule test charge (𝑙𝑖𝑚).
𝑞→0
The electric field strength describes the effect of
the charges creating the electric field (and we ignore
the electric field created by the test charge)
Reported in units of Newtons per Coulomb (N/C)
Quantifying Electric Field
𝐸=
𝐹
𝑞
So, 𝐸 =
where 𝐹 =
𝑄𝑞
𝑘 2
𝑟
𝑘𝑄𝑞
2
𝑟
𝑄
𝐸=𝑘 2
𝑟
𝑞
Strength of electric field is directly
proportional to strength of source charge Q
Strength of electric field is inversely
proportional to the square of the distance
from the source charge
Example
A proton (q=1.6 x 10-19 C) is released in a uniform electric field and
experiences an electric force of 1.86 x 10-14 N toward the south. What
is the magnitude of the field? What is its direction?
𝑞 = 1.6 𝑥
10−19 𝐶
𝐹 = 1.86 𝑥 10−14 𝑁
𝐹 1.86 𝑥 10−14 𝑁
𝐸= =
𝑞
1.6 𝑥 10−19 𝐶
𝐸 =?
𝐸 = 1.2 𝑥
𝑁
5
10
south
𝐶
Example
Determine the magnitude of acceleration experienced by an electron
(q=-1.6 x 10-19 C, m = 9.1 x 10-31 kg) in an electric field of 756 N/C.
𝑞 = −1.6 𝑥 10−19 𝐶
𝑚 = 9.1 𝑥 10−31 𝑘𝑔
𝑁
756
𝐶
𝐸=
𝑎 =?
𝐸=
𝐹
𝑞
where 𝐹 = 𝑚𝑎
So, 𝐸 =
𝑚𝑎
𝑞
so, 𝑎 = 𝐸
𝑞
𝑚
𝑁 −1.6 𝑥 10−19 𝐶
𝑎 = (756 )
𝐶 9.1 𝑥 10−31 𝑘𝑔
𝑎 = 1.32 𝑥
𝑚
14
10
/𝑠
𝑠
Electric Potential
Difference in Electrical Potential Energy
In the case of a spring or an
electric charge,
∆𝑈 = −𝑊
where 𝑊 = 𝐹𝑑
So, ∆𝑈 = −𝐹𝑑
where 𝐹 = 𝑞𝐸
So, ∆𝑈 = −𝑞𝐸𝑑
Difference in Electrical
Potential Energy
In the case of an electric charge,
∆𝑈 = −𝑞𝐸𝑑
Change in potential depends on the
distance between the two charges.
Change in potential depends on
the strength of the electric field
Change in potential depends
on size of test charge
Difference in Potential Energy / Charge
When describing forces induced by electric fields, it was useful to
introduce 𝐸 as the strength of field in terms of force per charge,
𝐹
.
𝑞
When dealing with differences in potential energy, it is useful to
describe measure it in terms of energy difference per charge.
Difference in Potential Energy / Charge
We introduce a new term
for difference in potential
energy per charge:
voltage, V
V≝
∆𝑈
𝑞
Frequently referred to
as ‘potential difference’
Measured in Joules per Coulomb
Abbreviated as volts, V
Named in honor of Alessandro Volta
(1745 – 1827), inventor of first batteries
Quantifying voltage – part 1
∆𝑈
V=
𝑞
So, ∆𝑈 = V𝑞
How much work can a
given charge do?
Cliff  Potential difference
height = potential energy
mass = potential energy
∆𝑈𝑔𝑟𝑎𝑣𝑖𝑡𝑦 = 𝑚𝑔ℎ
voltage= potential energy
charge= potential energy
∆𝑈𝑒𝑙𝑒𝑐𝑡𝑟𝑖𝑐 = 𝑞V
Typical voltages
Thundercloud
to ground
Van der Graaf
generator
108 V
106 V
High-voltage
powerline
Household
voltage (US)
105 V
120 V
batteries
1.5 to 9 V
Potential changes on
skin (EKG)
10-4 V
Example
A electron (q=1.6 x 10-19 C) is accelerated
through a potential difference of +5000 V in
old television. What is the change in
electrical potential energy?
−19
𝑞 = −1.6 𝑥 10
V = 5000 𝑉
∆𝑈 =?
𝐶
∆𝑈 = 𝑞V = (−1.6 𝑥 10
−19
𝐽
𝐶)(5000 )
𝐶
∆𝑈 = −8.0 𝑥 10−16 𝐽
Potential energy is lost by electron
(and converted into kinetic energy)
Quantifying voltage – part 2
∆𝑈 = −𝑞𝐸𝑑
So, V
Or, 𝐸
= −𝐸𝑑
=
V
−
𝑑
Electric field strength is
frequently reported in
volts / meter
Example
An electric field of 525 V/m is desired between two parallel plates that
are 11.0 mm apart. How large a voltage should be applied?
𝑑 = 11.0 𝑚𝑚
= 1.1 𝑥 10−2 𝑚
𝑉
525
𝑚
𝐸=
V =?
𝑉
V = −𝐸𝑑 = −(525 )(1.1 𝑥 10−2 𝑚)
𝑚
V = −5.8 𝑉
Note the convention: voltage, V
volts, V (italicized)
Implications
If you know the voltage difference
and the distance between two
plates, you can calculate the
strength of the electric field…
• And make capacitors
• And electrocardiograms
• And oscilloscopes
• And televisions
• And mass spectrometers
Etc.