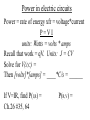* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Winter wk 3 – Thus.20.Jan.05
Magnetohydrodynamics wikipedia , lookup
Eddy current wikipedia , lookup
Electric charge wikipedia , lookup
Superconductivity wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
Photovoltaics wikipedia , lookup
Wireless power transfer wikipedia , lookup
Electroactive polymers wikipedia , lookup
Electromagnetism wikipedia , lookup
Static electricity wikipedia , lookup
Hall effect wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electric machine wikipedia , lookup
Geomagnetic storm wikipedia , lookup
Electrification wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
General Electric wikipedia , lookup
Earthing system wikipedia , lookup
History of electric power transmission wikipedia , lookup
Insulator (electricity) wikipedia , lookup
Electrostatics wikipedia , lookup
Opto-isolator wikipedia , lookup
Stray voltage wikipedia , lookup
Electric current wikipedia , lookup
History of electrochemistry wikipedia , lookup
Mains electricity wikipedia , lookup
Electricity wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
Electromotive force wikipedia , lookup
Winter wk 3 – Thus.20.Jan.05 • • • • Ch.24: Voltage and electric field Ch.26: Current and resistance Solar applications Ch.27: Circuits Energy Systems, EJZ Equipotential surfaces and E fields Equipotential = constant voltage Conductors are equipotentials, in electrostatics Potential difference Electric field dV/dx = -E or, equivalently, V E dr Practice: Ch.24 Q5,8 (p.646), P#3, 4, 6, 35 Ch.24 #4 Ch.24 #6 Ch.24 #35 Electrostatics (d/dt=0): charges fields forces, energy E.dA = q/0=, E = F/q V (r ) 1 (r ' ) 4 d ' E dl E V F=qE=ma W = qV, C = q/V • Charges make E fields and forces • charges make scalar potential differences dV • E can be found from V • Electric forces move charges • Electric fields store energy (capacitance) Ch.26: Currents and Resistance Current = rate of flow of charge I = dq/dt Units: amps = coulombs/sec Current density: J = current/area = n e v Ch.26 Q1, 2, P.1, 8 Water flow: pressure volume/time Electricity flow: voltage V current I Ch.26: Q1, 2, P.1, 8 Resistance Resistance = resistivity * area/length R = * A/L Which conductor has the greatest resistivity? Ch.26: Q3 Ohm’s law In many substances, for a given resistance R, the stronger the driving voltage, the greater the current that flows: Voltage = current * resistance V=I*R Ch.26 Q5, P.17 Power in electric circuits Power = rate of energy xfr = voltage*current P=VI units: Watts = volts * amps Recall that work = qV. Units: J = CV Solve for V(J,C) = Then [volts]*[amps] = ____*C/s = ______ If V=IR, find P(I,R) = Ch.26 #35, 64 P(R,V) = Ch.27: Circuits: Battery pumps electricity current flows http://hyperphysics.phy-astr.gsu.edu/hbase/electric/watcir.html#c1 Voltage = emf Voltage = potential difference Electromotive force = V = dW/dq =work done per unit charge d/dx = -E = electric field Emf and electric field E d/dx = -E = electric field Using the fundamental theorem of calculus, we can derive another of Maxwell’s eqns: d E dx d dx dx E dx E dx Ch.27: Practice with simple circuits Q2 #5, 14 Solar applications Storms from the Sun: p.13: If a CME travels at 1 million miles per hour, how long does it take to reach Earth? p.16: The 2 May 1994 event dumped 4600 GW-hr of electricity into Earth’s upper atmosphere. How much energy is that in Joules? p.16: If the Earth’s mean magnetic field is B0=0.5 Gauss, and one Tesla=104 Gauss, by what percent does 2000 nanoTesla change Earth’s field? p.54: For the CME of 1 Sept 1859: calculate its speed v, if it took 18 hours to reach Earth. more Solar applications Storms from the Sun: p.77: If Rsun = 100 REarth, then find the ratio of their volumes, Vsun/VEarth p.77: If m=5 millions tons of mass is converted to energy (E=mc2) each second, calculate the power (P) produced by the Sun. p.82: If the Sun’s mass is M=2x1030 kg, and it keeps losing dm/dt = 5 million tons per second, how long (T) can the Sun last? p.83: If the solar wind pours I=1 million amps into Earths magnetosphere, how much charge (Q) is that per day? Extra solar applications p.13: Calculate vthermal from Tsolar wind. Compare to vflow. p.16: Derive the altitude for a geosynchronous orbit p.77: If the Sun’s core temperature is about T=107K, calculate the thermal speed vth of protons in the core.