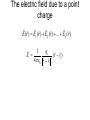Download Chapter 24 Electric Fields

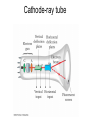
Chapter 24 Electric Fields
第二十四章 電場
Action at a distance
kq1q2
F12  2 rˆ21
r21
k  9.0 10 Nm / C
9
r̂21
2
2
q1
q1
q2
q2
Another point of view -- Fields
kq1q2
F12  2 rˆ21
r21

 
F12  q1 E2 (r21 )
  kq2
1 q2
E2 (r )  2 rˆ 
rˆ
2
r
40 r
where E2 is the electric field generated by charge q2 and r is a
position vector from the position of q2 to any point in space.
 0  8.854 1012 C 2 / Nm2
Electric field lines
Electric field lines
The concept of electric field lines was originally due to Faraday who
envisioned that the space around a charge is filled with “lines of force”.
The field lines are originated from positive charges and terminated at
negative charges, and they are unbroken in vacuum.
The relationship between the
electrical field and field lines
Electric field lines with arrows indicate the local field directions, and
their density in a plane perpendicular to the local field represents the
magnitude of the local field.
Suppose that there are N field
lines originated from a positive
charge q, then we have the
density of field lines given by
N / 4πr2 at a distance r from the
charge.
Note that if N = q / ε0 then we
recover E = q / 4πε0 r2.
Field lines repel each other
Field lines are smooth
The electric field due to a point
charge
 
   
 
E(r )  E1 (r )  E2 (r )  ...  En (r )

Ei 
 
(r  ri )


3
40 r  ri
1
qi
Sample problem
What is the electric field at point P?
Sample problem
What is the electric field at point P?
The electric field due to
an electric dipole
y
P
E
r
-a
r
r
q
(
r  r
4 0 r  r
r  axˆ
a
x
3

r  r
r  r
3
r  axˆ
Electric dipole moment:
p  q(r  r )  2qaxˆ
p  2qa
)
The electric field due to an electric
dipole
Along x-axis:
For
r  xxˆ
2x p
E
4 0 ( x 2  a 2 ) 2
1 2p
x  a : E 
4 0 x3
x  a:
1
1 ( a 2  x 2 ) p
For x  a : E 
4 0 a(a 2  x 2 )2
The electric field due to an electric
dipole
r  yyˆ  zzˆ
1
p
E
4 0 ( y 2  z 2  a 2 )3/ 2
In y-z plane:
r  a :
Note that
E
1
E 2
r
1
E 3
r
1 p
4 0 r 3
for net charge  0
for net charge  0
but net dipole moment  0
Electric field due to a line of charge
Electric field due to a line of charge
Electric field due to a line of charge
Electric field due to a line of charge
Electric field due to a charge disk
A point charge in an electric field
F  qE
Millikan oil-drop experiment (1910-1913)
Cathode-ray tube
Deflecting charge particles
A dipole in an electric field
pH2O  6.2 1030 Cm
A dipole in an electric field
There is no net force on a dipole.
But there is a torque.
  qEa sin   (qE )(a sin  )
 pE sin 
  p E
Potential energy of a dipole in a
uniform electric field
U   pE cos 
U ˆ
  (
)   pE sin ˆ

Home work
Question (問題): 6, 8, 19
Exercise (練習題): 5, 10, 16
Problem (習題): 8, 18, 31, 32