Download Fields - HRSBSTAFF Home Page

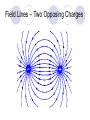
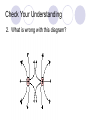
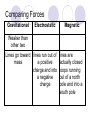
Field Theory
Physics 12
Field Theory
When forces exist without contact, it can
be useful to use field theory to describe
the force experienced by a particle at any
point in space
We have previously considered
gravitational fields and seen that
gravitational fields are the result of mass
creating the field and the distance an
object is placed from the mass
Draw a diagram of what you think a
gravitational field would look like.
Fields
There are three common forces that act
without contact between objects:
Gravitational
Electrostatic
Magnetic
Since these forces do not require contact,
field theory is often used to describe the
force that results on an object within the
field (ie, not touching)
How do we know what a field looks like
then???
Electric Field Mapping
 To map an electric field, a small test charge is
placed in the field and the magnitude and
direction of the force is recorded
 The test charge is then moved throughout the
electric field and a map of the field is created
 The force experienced by the test charge will be
the result of Coulomb’s Law
 Test charge is a positive charge
Imagine a positively charged particle…
Electric Field Mapping
If a positive charge was put in this field, it
would repel (outward arrows).
As you get farther from
the charged particle, the
repulsion gets less and
less.
The arrows represent the
FORCE.
What would a negatively charged
particle’s field look like?
Test Charge
 The test charge that is used
must be small compared to the
charge creating the field
 If not, the test charge’s field will
change the field that is being
investigated
 The electric field should be the
same regardless of the test
charge used
Multiple charges in a field
 What would a field look like for one positively and one
negatively charged particle?
Field Lines – Two Opposing Charges
How do I know the arrow points to the –
not +?
Positively charged particles create
outward arrows and vice versa
What do you think…
Will happen when two positive charges of
equal strength are put together? What will
the field look like?
Field Lines – Two Positive Charges
What do you think…
Will happen when two positive charges are
put together? What will the field look like?
Problem
 What are the relative
magnitudes of the
charges in the
diagram?
 What is the polarity of
each of the charges?
*** NOTES
More dense field lines means greater
charge
Electric field lines never cross each other
Multiple Charges
 It is also possible to
consider what
happens with multiple
charges:
Check Your Understanding
1.Several electric field line patterns are
shown in the diagrams below. Which of
these patterns are incorrect? Why?
C, D, E
Check Your Understanding
2. What is wrong with this diagram?
d
DAECB
Objects A, C, F, G, H and I are positive.
B<A
C<D
G<E<F
J<H<I
Test Charge – Electric Field Intensity
Formula
kqqt
 q is the charge of the source
Fe  2
 qt is the charge of the test
r
charge
Fe kqqt

2
qt qt r
 Divide your electrostatic
force formula by the test
charge
 E = Fe/qt
 This is the electric field
intensity
Fe kq
 2
qt r

 Fe
E
qt
Where …
E = electric field intensity (N/C)
FQ = Fe = electric force (N)
qt = Electric charge (C) of test charge
Field Intensity at a Point
Example 1: A positive charge of 3.2 x 10 5 C experiences a force of 4.8N right when
placed in an electric field. Find the
magnitude and direction of the field, at
that location.
Draw a picture of what this might look like.
Example 2
A positive test charge, qt = + 2.0 x 10-9 C,
is placed in an electric field and
experiences a force of F = 4.0 x 10-9 N
[W].
A) What is the electric field intensity at the
location of the test charge?
B) Predict the force that would be
experienced by a charge of +9.0 x 10-6 C if
it replaced the test charge.
Answer
Practice Problems
Page 646
Questions 12-14
So what do you think would happen…
If we wanted a diagram of Earth and Moon
(gravitational charge instead of
electrostatic)?
What do you think…
A field would look like around a “regular”
magnet (one North and one South pole)?
Comparing Forces
Gravitational
Electrostatic
Magnetic
Attractive
Attractive or
repulsive
Inverse square
behaviour
Depends on
charge
Attractive or
repulsive
Inverse square
behaviour
Depends on
pole strength
Inverse square
behaviour
Depends on
mass
Comparing Forces
Gravitational
Electrostatic
Weaker than
other two
Lines go toward lines run out of
mass
a positive
charge and into
a negative
charge
Magnetic
lines are
actually closed
loops running
out of a north
pole and into a
south pole
Field Lines Summary
 Graphical representation of the field
surrounding a point charge/mass or series of
charges/poles
 Electric fields: lines run out of a positive charge
and into a negative charge
 Gravitational fields: lines all go toward a mass
 Magnetic field lines: lines are actually closed
loops running out of a north pole and into a
south pole
Gravitational Field
 The strength of a
gravitational field can be
determined using a test
mass
 Like with a test charge, the
test mass should be small
 In a manner similar to the
electric field, we will divide
out the test mass
Gmmt
Fg 
2
r
Fg Gmmt

mt r 2
mt
Fg
Gm
 2
r
mt

 Fg
g
mt
Practice Problems
Page 649
Questions 15-18, 19*** (challenge – remember
centripetal acceleration!)