Download PPT - LSU Physics & Astronomy

Physics 2113
Jonathan Dowling
Lecture 42: FRI 05 DEC
Final Exam Review
The Grading
•
•
•
•
Midterms Final Exam
Homework
In Class PP
100 points each
- 200 points
- 75 points
- 25 points
TOTAL: 600 points
• Numerical Grade: Total Points / 6
• A: 90–100
B: 75–89
C: 60–74
D: 50–59
F: <50
Final Exam
• 5:30PM-7:30PM MON 08 DEC
• Cox Auditorium
• ≥ 50 % of Exam From HW01-14
• 100 PTS: CH 13, 21–30
• 100 PTS: CH 31–33
• At least 1 Problem from Exam I, II, or III
Final Exam
• 8 Questions & 6 Problems
• Questions are labeled “Question” are multiple
choice or similar and no partial credit.
• Problems are labeled “Problem” and you must
show all your work to get any partial credit. In
particular an answer in a problem with no
explanation or no work will result in no credit.
What do you need to make on the final to get an A, B, C, etc.?
A: 90–100
B: 75–89
C: 60–74
D: 50–59
F: <50
Solve this simple equation for x:
é mt1+ mt2 + mt 3 + (hw / 450) ´ 75
ù
ê + max[(icppc – icppx) / icpp, 0] ´ 25 + x ú / 6 = y
)
ë (
û
Where mt1=exam1, mt2=exam2, mt3=exam3, hw=total points
on your hws01–14 (out of 450), icppc=checks, icppx=X’s,
icpp=number of times you were called on, max is the binary
maximum function, and y is your desired cutoff number, y = 90,
75, 60, or 50. Then x is the score out of 200 you need on the
final to make that cutoff grade y. This assumes no curve.
Example: John Doe wants to know what he needs to make on
the final in order to get an A = 90 in this class.
mt1 = 81
mt2 = 70
mt 3 = 90
hw = 435
icppc = 3
icppx = 0
icpp = 3
max[(icppc - icppx) / icpp, 0] = max[1,0] = 1
{( 81+70+90 ) +[ (435/450) ´ 75 ] +(1´ 25 ) + x} = 90
Solve: x = 201.5 / 200 > 100%
It is very likely impossible for John to get an A as he’d need better than a
perfect score on the final. How good does he need to do to avoid a C = 74?
{( 81+70+90 ) +[(435/450) ´ 75 ] +(1´ 25 ) + x} = 75
Solve: x = 111.5 / 200 = 56%
John is extremely unlikely to get an A, and is unlikely to get a C, so the
most probable outcome is that John will get a B in this class.
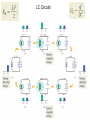
LC Circuits
PHYS2113 An Electromagnetic LC Oscillator
Capacitor initially charged. Initially, current is zero,
energy is all stored in the E-field of the capacitor.
Energy Conservation: Utot = U B +UE
A current gets going, energy gets split between the
capacitor and the inductor.
1 2
1 q2
U B = L i U E =
2
2C
Capacitor discharges completely, yet current keeps going.
Energy is all in the B-field of the inductor all fluxed up.
The magnetic field on the coil starts to deflux, which
will start to recharge the capacitor.
1 2 1 q2
Utot = L i +
2
2C
Finally, we reach the same state we started with (with
opposite polarity) and the cycle restarts.
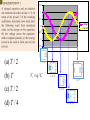
1.5
1
0.5
Charge
0
Time
-0.5
Current
-1
-1.5
(a) T / 2
(b) T
(c) T / 2
(d) T / 4
t=0
Vc = q / C
t =T /4
t =T
t =T /2
t = 3T / 4
Electric Oscillators: the Math
q = q0 cos(w t + j 0 )
Amplitude = ?
i(t) = q¢(t) = -q0w sin(w t + j 0 )
i¢(t) = q¢¢(t) = -w q0 cos(w t + j 0 )
2
Energy as Function of Time
Voltage as Function of Time
1
1
2
2
U B = L [ i ] = L [ q0w sin(w t + j 0 )] VL = Li¢(t) = -Lw 2 q0 cos(w t + j 0 )
2
2
1 [ q]
1
2
UE =
=
q
cos(
w
t
+
j
)
[0
0 ]
2 C
2C
2
1
1
VC = [ q(t)] = [ q0 cos(w t + j 0 )]
C
C
Example
• In an LC circuit,
L = 40 mH; C = 4  F
• At t = 0, the current is a
maximum;
• When will the capacitor
be fully charged for the
first time?
1.5
1
0.5
Charge
0
Time
-0.5
Current
-1
-1.5
t=0
t =T /4
t =T /2
t = 3T / 4 t = T
w=
1
1
=
rad/s
LC
16x10 -8
•  = 2500 rad/s
• T = period of one
complete cycle
•T =  = 2.5 ms
• Capacitor will be
charged after T=1/4
cycle i.e at
• t = T/4 = 0.6 ms
Example
• In the circuit shown, the switch is in
position “a” for a long time. It is
then thrown to position “b.”
• Calculate the amplitude  q0 of the
resulting oscillating current.
1 mH
1 mF
b
E=10 V
a
i = -w q0 sin(w t + f0 )
• Switch in position “a”: q=CV = (1 mF)(10 V) = 10 mC
• Switch in position “b”: maximum charge on C = q0 = 10 mC
• So, amplitude of oscillating current =
1
w q0 =
(10mC) = 0.316 A
(1mH)(1mF)
Damped LCR Oscillator
Ideal LC circuit without resistance: oscillations
go on forever;  =
C
(LC)–1/2
L
R
Real circuit has resistance, dissipates energy:
oscillations die out, or are “damped”
Math is complicated! Important points:
– Frequency of oscillator shifts away from
1.0
 = (LC)-1/2
0.8
 QLCR=2L/R
– For small damping, peak ENERGY decays
with time constant
 ULCR= L/R
UE
– Peak CHARGE decays with time constant =
Umax
Q 2 - RtL
=
e
2C
0.6
0.4
0.2
0.0
0
4
8
12
time (s)
16
20
R2
1
≪
?
2
LC
4L
3
8
10 ≪ 10 !
w¢ =
1
R2
@
LC 4L2
1
=w
LC
Q(t)
1 2 3
•••
13
Q(0) / 2 = 50%
t(s)
Example, Transformer:
Displacement “Current”
Maxwell proposed it based on
symmetry and math — no experiment!
B
B!
B
i
i
E
Changing E-field Gives Rise to B-Field!
32.3: Induced Magnetic Fields:
Here B is the magnetic field induced along a
closed loop by the changing electric flux FE
in the region encircled by that loop.
Fig. 32-5 (a) A circular parallel-plate capacitor, shown in side view, is being charged by
a constant current i. (b) A view from within the capacitor, looking toward the plate at
the right in (a).The electric field is uniform, is directed into the page (toward the plate),
and grows in magnitude as the charge on the capacitor increases. The magnetic field
induced by this changing electric field is shown at four points on a circle with a radius r
less than the plate radius R.
Ba > Bc > Bb > Bd = 0
dF E d
dE
= EA = A
µ slope
dt
dt
dt
Example, Magnetic Field Induced by
Changing Electric Field:
Example, Magnetic Field Induced by Changing Electric
Field, cont.:
32.4: Displacement Current:
Comparing the last two terms on the right side of the above equation shows that the
term
must have the dimension of a current. This product is usually treated as
being a fictitious current called the displacement current id:
in which id,enc is the displacement current that is encircled by the integration loop.
The charge q on the plates of a parallel plate capacitor at any time is related to the
magnitude E of the field between the plates at that time by
in which A is
the plate area.
The associated magnetic field are:
AND
Example, Treating a Changing Electric Field as a Displacement Current:
The displacement current id = i is
distributed evenly over grey area.
So rank by i
enc
d
= amount
of grey area enclosed by each loop.
d =c>b>a
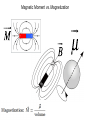
Magnetic Moment vs. Magnetization
32.10: Paramagnetism:
The ratio of its magnetic dipole moment to its
volume V. is the magnetization M of the sample,
and its magnitude is
In 1895 Pierre Curie discovered experimentally
that the magnetization of a paramagnetic sample
is directly proportional to the magnitude of the
external magnetic field and inversely
proportional to the temperature T.
is known as Curie’s law, and C is called the
Curie constant.
Mathematical Description of Traveling EM Waves
Electric Field:
Magnetic Field:
E = Em sin (kx - w t )
B = Bm sin (kx - w t )
Wave Speed:
c=
m0e 0
All EM waves travel a c in vacuum
Wavenumber: k =
EM Wave Simulation
1
w
=
c
2p
l
2p
Angular frequency: w =
T
Vacuum Permittivity: e 0
Vacuum Permeability:
Fig. 33-5
Amplitude Ratio:
Em
=c
Bm
Magnitude Ratio:
E (t )
=c
B (t )
m0
(33-5)
The Poynting Vector:
Points in Direction of Power Flow
Electromagnetic waves are able to transport energy from transmitter
to receiver (example: from the Sun to our skin).
The power transported by the wave and its
direction is quantified by the Poynting vector.
John Henry Poynting (1852-1914)
For a wave, since
E is perpendicular to B:
Units: Watt/m2
| S |=
1
m0
EB =
1
cm 0
E2
In a wave, the fields change
with time. Therefore the
Poynting vector changes
too!!
The direction is constant, but
the magnitude changes from
0 to a maximum value.
EM Wave Intensity, Energy Density
A better measure of the amount of energy in an EM wave is obtained by
averaging the Poynting vector over one wave cycle.
The resulting quantity is called intensity. Units are also Watts/m2.
I =S =
1
cm 0
___
2
E =
1
cm 0
__________ __
2
2
Em sin (kx - wt )
The average of sin2 over
one cycle is ½:
1
I=
Em 2
2cm0
Bm = Em / c
Both fields have the
same energy density.
1
1
1
B2
1 B2
2
2
uE = e 0 E = e 0 (cB) = e 0
=
= uB
2
2
2 e 0 m0 2 m0
The total EM energy density is then
u = e 0 E = B / m0
2
2
EM Spherical Waves
The intensity of a wave is power per unit area. If one has a
source that emits isotropically (equally in all directions) the
power emitted by the source pierces a larger and larger
sphere as the wave travels outwards: 1/r2 Law!
I=
Ps
4pr
2
So the power per
unit area decreases
as the inverse of
distance squared.
Example
A radio station transmits a 10 kW signal at a frequency of 100 MHz.
Assume a spherical wave. At a distance of 1km from the antenna, find the
amplitude of the electric and magnetic field strengths, and the energy
incident normally on a square plate of side 10cm in 5 minutes.
Ps
10 ´10 3 W
2
I=
=
=
0.8mW
/
m
4p r 2 4p (1´10 3m)2
1
2
I=
Em Þ Em = 2cm0 I = 0.775V/m
2cm0
Bm = Em / c = 2.58 nT
Radiation Pressure
Waves not only carry energy but also momentum. The effect is
very small (we don’t ordinarily feel pressure from light). If light
is completely absorbed during an interval Δt, the momentum
Transferred Δp is given by
Du
and twice as much if reflected.
Dp =
Newton’s law:
Dp
F=
Dt
c
F
A
I
Now, supposing one has a wave that hits a surface
of area A (perpendicularly), the amount of energy
transferred to that surface in time Δt will be
DU = IADt
Radiation
pressure:
IADt
D
p
=
therefore
c
IA
F=
c
I
2I
pr = (total absorption), pr =
(total reflection)
c
c
[Pa=N/m2]
The pressure p is independent
of the area A.
(a) The pressure remains the same.
The force F is proportional
to the area A.
(b) The force decreases.
EM waves: polarization
Radio transmitter:
If the dipole antenna
is vertical, so will be
the electric fields. The
magnetic field will be
horizontal.
The radio wave generated is said to be “polarized”.
In general light sources produce “unpolarized
waves”emitted by atomic motions in random
directions.
EM Waves: Polarization
Completely unpolarized light will have
equal components in horizontal and vertical
directions. Therefore running the light through
a polarizer will cut the intensity in half: I=I0/2
When polarized light hits a polarizing sheet,
only the component of the field aligned with the
sheet will get through.
E y = E cos(q )
And therefore:
I = I 0 cos 2 q
Example
Initially unpolarized light of
intensity I0 is sent into a system of
three polarizers as shown. What
fraction of the initial intensity
emerges from the system? What
is the polarization of the exiting
light?
• Through the first polarizer: unpolarized to polarized, so I1=½I0.
• Into the second polarizer, the light is now vertically polarized. Then, I2 =
I1cos2(60o)= 1/4 I1 = 1/8 I0.
• Now the light is again polarized, but at 60o. The last polarizer is
horizontal, so I3 = I2cos2(30o) = 3/4 I2 =3 /32 I0 = 0.094 I0.
• The exiting light is horizontally polarized, and has 9% of the original
amplitude.
Completely unpolarized light will have
equal components in horizontal and vertical directions.
Therefore running the light through first polarizer will cut the
intensity in half: I=I0/2
When the now polarized light hits second
polarizing sheet, only the component of the field
aligned with the sheet will get through.
(a) I 0 ® 12 I 0 ® 12 I 0 cos2 (0°) = 12 I 0
(b) I 0 ® 12 I 0 ® 12 I 0 cos2 (60°) = 18 I 0
(c) I 0 ® 12 I 0 ® 12 I 0 cos2 (90°) = 0
(d) I 0 ® 12 I 0 ® 12 I 0 cos2 (30°) = 83 I 0
I = I 0 cos2 q
First polarizer cuts intensity in half.
Second cuts by cos 2 q .
The q is angle between dashed lines.
More gets through when more aligned.
Less gets through when less aligned.
a>d >b>c=0