Download Lecture 8 ppt version

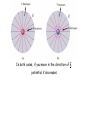
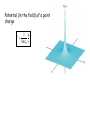
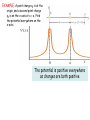
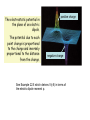
ADVANCE WARNING!
THERE WILL BE A MID-SEMESTER TEST
DURING THE WEDNESDAY WORKSHOP
10 NOVEMBER
11 AM
PHYSICS LECTURE THEATRE A
It is worth 10% of your final mark for this
course
LAST LECTURE CHECKPOINT: A ball of charge –50e lies at the
centre of a hollow spherical metal shell that has a net charge
of –150e.
True: A
False: F
The charge on the shell’s inner surface is +50e
True
The charge on the shell’s outer surface is –150e False
Answers: (a) +50e
(b) –200e
Electric Potential
Chapter 22
Electric potential energy
Electric potential difference
Equipotential surfaces
Potential due to a point charge
Potential due to a group of point charges
Calculating the field from the potential
Electric Potential Energy
CHECKPOINT: A proton moves from
point i to point f in a uniform
electric field directed as shown.
Does the electric field do
A. positive or
B. negative work on the proton?
Does the electric potential energy of the proton
A. increase or
B. decrease?
Answers:
B.
the field does
negative work
A.
the potential
energy increases
When an electrostatic force acts between two or more charged particles
within a system of particles, we can assign an Electric Potential Energy U to
the system.
If the system changes from initial state, i, to final state, f, the electrostatic
force does work W on the particles.
U = Uf – Ui = -W
The force is conservative, and therefore the work done is path-independent.
We take a reference potential energy to be when the system of particles are
all infinitely separated from each other, and is set to be zero. Ui = 0 and so
U = Uf = -W
where W is the work done on the particle by the electrostatic forces during
the move in from infinity
Electric Potential
The potential energy of a charged particle in an electric
field depends on the size of the charge. If we increase
the charge, then the potential energy is increased, but
we have the same potential energy per unit charge.
The potential energy per unit charge has a unique value
at any point in an electric field.
V
U
q
Potential
(NB scalar)
This is independent of the charge and characteristic
only of the electric field under investigation.
The electric potential difference V between any two points i and f in
an electric field is :
V = Vf –Vi = U/q = -W/q
Definition of potential difference
This is the negative of the work done by the electrostatic force to
move a unit charge from one point to another.
V
 W
q
Definition of potential
where W is the work done by the electric field on a charged
particle that moves in from infinity to point f.
In both cases, if you move in the direction of E,
potential V decreases
NB Electric Potential V and Electric Potential Energy U
are quite different quantities and must not be confused!
 Electric Potential V is a property of an electric field,
regardless of whether a charged object has been placed in the
field. It is measured in Joules/Coulomb or Volts.
 Electric Potential Energy U is an energy of a charged object
in an external field. It is measured in Joules.
Calculating the Potential from the Field
A test charge q0 moves
from point i to point f in a
non-uniform electric
field.
During displacement ds a
force q0E acts on the test
charge.
f
V   E  d s
i
Fill in on the handouts
The electric field points in
the direction in which the
potential decreases most
rapidly.
If a positive test charge q0
is in an electric field, it
accelerates in the
direction of the field.
If it is released from rest,
its kinetic energy
increases and its potential
energy decreases.
f
V   E  d s
i
UNITS
SI unit for potential and potential difference is the Volt
1 V = 1 J/C
Dimensions of potential are also those of electric field
times distance. Therefore, the unit of electric field is
equal to one volt per metre.
1 N/C = 1 V/m
So we can think of the electric field strength as either a
force per unit charge, or as a rate of change of V with
respect to distance.
We define an energy unit that is convenient for
energy measurements using elementary particles
such as electrons and protons.
Potential due to a point charge
Find the electric potential
due to a particle of charge
q, at a radial distance r
from the particle
f
V   E  d s
i
Potential due to a point charge
Find the electric potential
due to a particle of charge
q, at a radial distance r
from the particle
f
V   E  d s
i
1
q
V
40 r
NB the sign of V is the
same as q
Fill in on the handouts
Potential (in the field) of a point
charge
1
q
V
40 r
Potential due to a group of point charges
We can find the electric potential due to a group of point
charges from the superposition principle. We calculate
the potential resulting from each charge at a given point
separately, with the sign of the charge included. We then
sum the potentials.
NB algebraic, not a vector sum
CHECKPOINT: The figure shows three arrangements of two
protons. Rank them according to the net electric potential
produced at point P by the protons, greatest first.
Answer: all equal as protons are the
same distance from P
EXAMPLE : A point charge q1 is at
the origin, and a second point
charge q2 is on the x-axis at x = a.
Find the potential everywhere on
the x-axis.
Picture the problem:
The total potential is the sum of
the potential due to each charge
separately.
EXAMPLE: A point charge q1 is at the
origin, and a second point charge
q2 is on the x-axis at x = a. Find
the potential everywhere on the
x-axis.
x
The potential is positive everywhere
as charges are both positive
The electrostatic potential in
the plane of an electric
dipole.
The potential due to each
point charge is proportional
to the charge and inversely
proportional to the distance
from the charge.
positive charge
negative charge
See Example 22.5 which derives V(r,θ) in terms of
the electric dipole moment p.