Download Target (R)

Stochastic Games
Krishnendu Chatterjee
CS 294
Game Theory
Games on Components.

Model interaction between components.

Games as models of interaction.

Repeated Games: Reactive Systems.
Games on Graphs.

Today’s Topic:



Games played on game graphs.
Possibly for infinite number of rounds.
Winning Objectives:


Reachability.
Safety ( the complement of Reachability).
Games.


1 Player Game : Graph G=(V,E) . R µ V which is the
target set.
2 Player Game: G=(V,E, (V,V})). Rµ V. (alternating
reachability).
Games.




1 Player Game : Graph G=(V,E) . R µ V which is the
target set.
1-1/2 Player Game (MDP’s) : G=(V,E,(V,V°)). Rµ V.
2 Player Game: G=(V,E, (V,V})). Rµ V. (alternating
reachability) .
2-1/2 Player Game: G=(V,E,(V,V},V°)). Rµ V.
1-1/2 player game
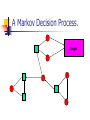
Markov Decision Processes.
•
A Markov Decision Process (MDP) is defined as follows:
•
G=(V,E, (V, V°) R)
•
(V,E) is a graph.
•
(V, V°) is a partition.
•
Rµ V – set of Target nodes.
•
V° are random nodes chooses between successors
uniformly at random.
•
For simplicity we assume our graphs are binary.
A Markov Decision Process.
Target
Strategy.

1: V* ¢ V ! D(V) such that for all
x 2 V* and v 2 V, if 1(x ¢ v) >0,
(v,1(x ¢ v) ) 2 E.
( D(V) is a probability distribution over
successor).
Subclass of Strategies.



Pure Strategy : Chooses one successor and not a
distribution.
Memoryless Strategy: Strategy independent of the
history. Hence can be represented as 1: V ! D(V)
Pure Memoryless Strategy is a strategy which is pure
and memoryless. Hence can be represented as
1: V ! V
Values.

Reach(R)={ s0 s1 … | 9 k. sk 2 R }

v1(s) =sup1 2 1 Pr1( Reach (R) )

Optimal Strategy: 1 is optimal if
v1(s) = Pr1 (Reach (R))
Values and Strategies.


Pure Memoryless Optimal Strategy exist. [CY 98, FV
97]
Computed by the following linear program.
minimize s x(s) subject to
x(s) ¸ x(s’)
(s,s’) 2 E and s 2 V
x(s) =1/2(x(s’)+x(s’’)) (s,s’), (s’s’’) 2 E and s 2 V°
x(s) ¸ 0
x(s)=1
s2R
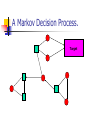
A Markov Decision Process.
Target
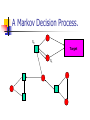
A Markov Decision Process.
S0
Target
S1
Pure Memoryless Optimal Strategy.



At s0 the player chose s1 and at s1 the
play reaches R with probability ½.
Hence the probability of not reaching R
in n steps is (1/2)n.
As n ! 1 this is 0 and hence the player
can reach with probability 1.
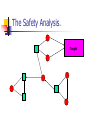
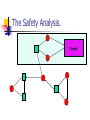
The Safety Analysis.
Target
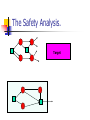
The Safety Analysis.
Target
The Safety Analysis.
Target
The Safety Analysis.



Consider the random player as an
adversary.
Then there is a choice of successors
such that the play will reach the target.
The probability of the choice of
successors is at least (1/2)n .
The Key Fact.

The Fact about the Safety Game:



If the MDP is a safety game for the player
and it loses with probability 1.
The number of nodes is n.
Then the probability to reach the target
within n steps is at least (1/2)n.
MDP’s.



Pure Memoryless Optimal Strategy
exists.
Values can be computed in polynomial
time.
The Safety game fact.
2-1/2 player games
Simple Stochastic Games.



G=(V,E,(V,V},V°)), Rµ V. [Con’92]
Strategy:
i:V* ¢ Vi ! D(V)
(as before)
Values:
v1(s)= sup1 inf2 Pr1,2(Reach(R))
v2(s)=sup2 inf1Pr1,2(: Reach(R))
Determinacy.



v1(s) + v2(s) =1 [Martin’98]
Strategy 1 for player 1 is optimal if
v1(s) = inf2 Pr1,2(Reach(R))
Our Goal: Pure Memoryless Optimal
Strategy.
Pure Memoryless Optimal Strategy.



Induction on the number of vertices.
Use Pure Memoryless strategy for
MDP’s.
Also use facts about MDP safety game.
Value Class.


Value Class is the set of vertices with
the same value v1. Formally,
C(p)={ s | v1(s) =p }
We now see some structural property of
a value class.
Value Class.
X
Higher
Value Class
Value Class
 maximize value
and } minimize
X
Lower
Value Class
Pure Memoryless Optimal Strategy.

Case 1. There is only 1 value class.


Case a: R = ; any strategy for player }(2)
suffice.
Case b: R  ; then since in R player (1)
wins with probability 1 then the values
class must be the value class 1.
One Value Class.
Target (R)
Favorable Subgame for Player 1: One Value Class.
Target (R)
K vertices.
Subgame Pure Memoryless Optimal Strategy.



By Induction Hypothesis: pure memoryless
optimal strategy in the subgame.
Fix the memoryless strategy of the sub-game.
Now analyse the MDP safety game.
For any strategy of player } (2) the probability
to reach the boundaries in k steps is at least
(1/2)k.
Pure Memoryless Optimal Strategy.


The optimal strategy of the subgame
ensures that the probability to reach the
target in original game in k+1 steps is
at least (1/2)k+1.
The probability of not reaching the
target within (k+1)*n steps is
(1-(1/2)k+1)n which is 0 as n ! 1.
More than One Value Class.
X
Higher
Value Class
Value Class
X
Lower
Value Class
More than One Value Class.
Higher
Value Class
Lower
Value Class
More than One Value Class.
Higher
Value Class
Lower
Value Class
Pure Memoryless Optimal Strategy.


Either can collapse a vertex in which
case we can apply induction hypothesis.
Else in no value class there is a vertex
for player 1 (V is empty)

Then it is a MDP and pure memoryless
optimal strategy of MDP suffice.
Computing the values.

Given a vertex s and value v’ if v1(s) ¸ v’
can be achieved in NP Å coNP.

Follows from pure memoryless optimal
strategy and that values of MDP’s can be
computed in polytime.
Algorithms for determining values.

Algorithms [Con’93]




Randomized Hoffman-Karp.
Non-linear programming.
All these algorithms practically efficient.
Open problem: Is there a polytime
algorithms to compute the values?
Limit Average Games.





r: V ! N (zero sum)
The payoff is limit average or mean-payoff
limn! 1 1/n i=1 to n r(si)
Two player mean payoff games can be
reduced to Simple Stochastic Reachability
Game. [ZP’96]
Two player Mean payoff games can be solved
in NP Å coNP.
Polytime algorithm is still open?
Re-Search Story.


2-1/2 Player Limit Average Pure Memoryless Strategy:

Gilette’ 57 : Wrong version of the proof.

Liggett & Lippman’ 69: New Correct Proof.
2 Player Limit Average Pure Memoryless Strategy



Ehrenfeucht & Mycielski ’78: “ didn’t understand”
Gurvich, Karzanov & Khachiyan ’88: “typo”
Zwick & Patterson ’96 : Quasi polynomial time algorithm
Slide Due to Marcin Jurdzinski
N-player games.

Pure Memoryless Optimal Strategy for 2
player zero-sum games can be used to prove
existence of Nash Equilibrium in n-player
games.



Key Idea: Threat Strategy as in Folk Theorem.
[TR’97]
No body has an incentive to change as other will
punish.
We require pure strategy to detect deviation.
Concurrent Games
Concurrent Games.


Previously games were turn-based
either player  or player } chose moves
or player ° chose successor randomly.
Now we allow the players to play
concurrently.
G=(S,Moves,1,2,)


i: S ! 2Moves n ;
: S £ Moves £ Moves ! S
A Concurrent Game.
Player 1 plays a,b and player 2 plays c,d
ad,bc
ac,bd
Concurrent games.


Concurrent Game with Reachability
Objective [dAHK’98]
Concurrent Game with arbitrary regular winning objective
[dAH’00,dAM’01]
A Concurrent Game.
Player 1 plays a,b and player 2 plays c,d
ad,bc
Deterministic (Pure) Strategy not Good:
a!d
b!c
ac,bd
A Concurrent Game.
Player 1 plays a,b and player 2 plays c,d
Randomized Strategy :a =1/2, b=1/2
ad,bc
1/2
1/2
ac,bd
c
Using arguments
as before pl.1
wins with prob. 1
1/2
d
1/2
Concurrent Games and Nash equilibrium.
ad
ac,bd
bc
Fact: For any strategy for player 1 he
cannot win with prob. 1.
As long player 1 plays move “a”
deterministically player 2 plays move “d”,
when player 1 plays “b” with positive
probability then player 2 plays “c” with
positive probability.
Thus (1,0) not a Nash Equilibrium.
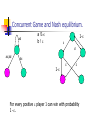
Concurrent Game and Nash equilibrium.
ad
a !1-
b!
1-
c
d
ac,bd
bc
1-


For every positive  player 1 can win with probability
1 -.
Why is “c” better?



If player 2 plays “d” then reaches target
with probability .
Probability of not reaching target in n
steps is (1-)n and this is 0 as n ! 1.
For move “c” player 1 reaches target
with probability (1-)
No Nash Equilibrium.


We saw earlier that (1,0) is not a Nash
equlibrium.
For any positive  we have (1-,) is not
a Nash equilibrium as player 1 can
choose a positive ’ <  and achieve
(1-’,’)
Concurrent Game: Borel Winning Condition.




Nash equilibrium need not necessarily exist but -Nash
equilibrium exist for 2-player concurrent zero-sum games for
entire Borel hierarchy. [Martin’98]
The Big Open Problem: Existence of -Nash equilibrium for nplayer / 2 player non zero-sum games.
Safety games: n-person concurrent game Nash equilibrium
exist.[Sudderth,Seechi’01]
Existence of Nash equilibrium and complexity issues for nperson Reachability game. (Research Project for this course)
Concurrent Games: Limit Average Winning Condition.


The monumental result of [Vieille’02]
shows -Nash equilibrium exist for 2player concurrent non-zero sum limit
average game.
The big open problem: Existence of Nash equilibrium for n-player limit
average game.
Relevant Papers.
1. Complexity of Probabilistic Verification : JACM’98 –
Costas Courcoubetis and Mihalis Yannakakis
2. The Complexity of Simple Stochastic Games: Information and
Computatyon’92 - Anne Condon
3. On algorithms for Stochastic Games – DIMACS’ 93
Anne Condon
4. Book: Competitive Markov Decision Processes. 1997
J.Filar and K.Vrieze
5. Concurrent Reachability Games : FOCS’98
Luca deAlfaro, Thomas A. Henzinger and Orna Kupferman
Relevant Papers
6. Concurrent - regular Games: LICS’00
Luca deAlfaro and Thomas A Henzinger
7. Quantitative Solution of  -regular Games : STOC’01
Luca deAlfaro and Rupak Majumdar
8. Determinacy of Blackwell Games: Journal of Symbolic Logic’98
Donald Martin
9. Stay-in-a-set-games : Int. Journal in Game Theory’01
S. Seechi and W. Sudderth ’01
10. Stochastic Games: A Reduction (I,II): Israel Journal in
Mathematics’02, N. Vieille
11. The complexity of mean payoff games on graphs: TCS’96 U.
Zwick and M.S. Patterson ’96
Thank You !!!

http:www.cs.berkeley.edu/~c_krish/