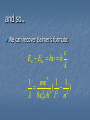* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download lect10
Renormalization group wikipedia , lookup
Ensemble interpretation wikipedia , lookup
Quantum state wikipedia , lookup
Geiger–Marsden experiment wikipedia , lookup
X-ray photoelectron spectroscopy wikipedia , lookup
James Franck wikipedia , lookup
Bremsstrahlung wikipedia , lookup
Renormalization wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Quantum teleportation wikipedia , lookup
Hidden variable theory wikipedia , lookup
Wave function wikipedia , lookup
Identical particles wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Electron configuration wikipedia , lookup
Elementary particle wikipedia , lookup
Tight binding wikipedia , lookup
Canonical quantization wikipedia , lookup
Atomic orbital wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Particle in a box wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Electron scattering wikipedia , lookup
Double-slit experiment wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Hydrogen atom wikipedia , lookup
Matter wave wikipedia , lookup
Wave–particle duality wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Quantum Physics… the world is about to get even weirder! Just when everything seemed to be working… Reading: Moore; Unit Q: chps 1-4 Lord Kelvin’s two small dark clouds: Michelson-Morley Experiment Blackbody radiation Planck’s Radiation Law Light (energy) is quantized … E = hf Blackbody spectrum explained! Working with quanta… Energy carried by light… En = nhf Energy quantization of a spring Wien’s Law and the Stefan-Boltzmann Law Light does not behave quite like a classical wave! …it gets weirder! The Photoelectric Effect Evidence that light behaves like a particle (sometimes)! Enter the photon Concept of the Work Function… Ek = hf - f When waves act like particles! The strange way in which photons interfere with themselves! Compton Scattering Light – is it: Wave Particle Both Neither? f q h 1 cosq mc When Particles act Like Waves! Prince Louis de Broglie makes a bold prediction The de Broglie wavelength: h p Confirmed by Davisson and Germer 1927 Particles, Waves and Quantons Particle and Wave are macro-world concepts “Quanton” is the quantum world actor The Great Heresy! A wave “is a particle” - A particle “is a wave” The Schroedinger Equation and Heisenberg’s Matrix Mechanics... ...a fundamental blurring of the universe It looks like Heisenberg - I think, I’m pretty sure, I’m not certain... The Uncertainty Principle h xp 4 h E t 4 The Copenhagen Interpretation... QM is a complete theory that tells us that the world, at the quantum level, is governed by statistical law. It rules out “classical” or “naïve” realist views of nature. As an example, consider the following applet demonstrating the Hydrogen atom. The Bohr Atom What do you do when theories fail? Our understanding of atoms and atomic physics circa 1910 currant buns, gold foil, “saturnalia” and others... Quantization the Nicholson atom Bohr applet demonstrating the Hydrogen atom. “as soon as I saw Balmer’s formula it all became clear to me” 1 1 1 R 2 2 2 n Bohr made two main postulates: an atom has a number of stable states in which the electrons orbit the nucleus in accordance with Newton’s Laws but do not radiate energy an atom emits or absorbs energy only when an electron moves from one stable state to another Bohr made a further auxilliary assumption electrons moved in orbits for which the orbital angular momentum was quantized... h l mvr n 2 In Bohr’s footsteps... forces energy momentum putting it all together... n h 0 rn me2 2 2 4 me En 2 2 2 8 0 h n and so.. We can recover Balmer’s formula: En Em h h 1 4 c me 1 1 2 3 ( 2 2) 8 0 ch l n taking stock... We can now: determine the size of the H atom predict the spectrum of H Can we extend this line of reasoning to other atoms: