Download Chapter 5 Sec. 2 Bohr`s Model and the Quantum Mechanical Model

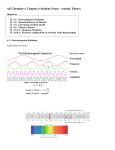
Chapter 5 Sec. 2 Bohr’s Model and the Quantum Mechanical Model NOTES

Bohr’s Model of the Atom
o Remember that the atomic emission spectra for hydrogen is discontinuous because it is made
up of certain frequencies of light.
 Scientists wanted to know WHY this was.
 In 1913 the Danish physicist named Niels Bohr answered this question and
correctly predicted the frequencies of the lines in hydrogen’s atomic emission
spectra.
o Energy States of Hydrogen
 Bohr proposed the following:

The lowest allowable energy level of an atom is called its ___________________
_______________________.
 When an atom gains energy it is said to be in an __________________________
_______________________.
 Bohr assigned a number, ______________, called a quantum number, to each orbit.
 The first orbit, the one closest to the nucleus, has a quantum number of n=1.
o The Hydrogen Line Spectrum
 When energy is added, the electron in an atom rises to an excited state.
 Equation used to calculate the change in energy between 2 energy levels:

Equation used to calculate the energy of a quantum, the energy of a photon, or the
energy difference between 2 levels:




E=
h = Planck’s constant =
c = speed of light =
λ=

Ex #1) A green light of wavelength 489 nm is observed in the emission spectrum of
hydrogen. Calculate the energy difference between the two energy states that are
responsible for this line.

Ex #2) The energy of one photon is 5.67 x 10-19 J. What is the length of the wavelength
observed?

Since only certain atomic energies are possible, only certain frequencies of
electromagnetic radiation can be emitted.
 Keep in mind that the energy levels are not evenly spaced.
o Drawings of Bohr’s Model of the Atom:

IMPORTANT: Bohr’s model was good, but it only explained the atomic emission spectra
of the hydrogen atom.

The Quantum Mechanical Model of the Atom
o Quantum Mechanical Model of the Atom:
o In 1924, a French physics student named Louis de Broglie explained the fixed energy levels of
Bohr’s model.
 He explained that electrons can act like _____________________________.
 He also showed that electrons on circular orbits can only have _____________________
numbers of wavelengths.
o de Broglie predicted that all moving particles have wave characteristics. de Broglie knew that if
an electron acted like a wave and was restricted to certain circular orbits that only certain
wavelengths, frequencies, and energies are possible.
 de Broglie Equation/ Particle Electromagnetic-Wave Relationship:
 λ=
 h = Planck’s constant =
 m=
 v=
o The Heisenberg Uncertainty Principle
 German physicist, Werner Heisenberg, showed that it is impossible to measure any
object without disturbing that object.
 The Heisenberg Uncertainty Principles states:

From the Heisenberg Uncertainty Principle we also understand that we can only know
the probability for an electron to occupy a certain region around the nucleus.
o The Schrodinger Wave Equation
 In 1926 the Austrian physicist Erwin Schrodinger came up with an equation that showed
hydrogen atom’s electron acting like a wave.


Each solution to the Schrodinger Wave Equation is called a wave function. The
wave function predicts the 3D region around the nucleus, called an atomic
orbital, where the electron is most likely to be found.
o An electron is most likely to be found:
The Bohr Model vs. The Quantum Mechanical Model of the Atom
BOHR MODEL
Scientist primarily
responsible for it
What electrons are
considered to be
Allowed energy
states/values
Electron pathways
QUANTUM MECHANICAL MODEL