* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Thinking Inside The Box: some experimental measurements in
Path integral formulation wikipedia , lookup
Quantum field theory wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Atomic theory wikipedia , lookup
Many-worlds interpretation wikipedia , lookup
Copenhagen interpretation wikipedia , lookup
Interpretations of quantum mechanics wikipedia , lookup
Coherent states wikipedia , lookup
Boson sampling wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Hidden variable theory wikipedia , lookup
History of quantum field theory wikipedia , lookup
Renormalization wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Matter wave wikipedia , lookup
Density matrix wikipedia , lookup
Canonical quantization wikipedia , lookup
Bell test experiments wikipedia , lookup
Probability amplitude wikipedia , lookup
Measurement in quantum mechanics wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum state wikipedia , lookup
Elementary particle wikipedia , lookup
EPR paradox wikipedia , lookup
Identical particles wikipedia , lookup
X-ray fluorescence wikipedia , lookup
Bell's theorem wikipedia , lookup
Quantum teleportation wikipedia , lookup
Double-slit experiment wikipedia , lookup
Wave–particle duality wikipedia , lookup
Bohr–Einstein debates wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Wheeler's delayed choice experiment wikipedia , lookup
Quantum entanglement wikipedia , lookup
Quantum key distribution wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Thinking Inside The Box:
some experimental measurements in quantum optics
Aephraim M. Steinberg
Centre for Q. Info. & Q. Control
Institute for Optical Sciences
Dept. of Physics, U. of Toronto
BEYOND workshop (tomorrow, 2007)
DRAMATIS PERSONÆ
Toronto quantum optics & cold atoms group:
Postdocs: An-Ning Zhang( IQIS) Morgan Mitchell ( ICFO)
(HIRING!)
Matt Partlow(Energetiq)Marcelo Martinelli ( USP)
Optics: Rob Adamson
Lynden(Krister) Shalm
Xingxing Xing
Kevin Resch(Wien UQIQC)
Jeff Lundeen (Oxford)
Reza Mir (geophysics)
Stefan Myrskog (BEC ECE)
(SEARCHING!)Mirco Siercke ( ...?)
Ana Jofre(NIST UNC)
Samansa Maneshi
Chris Ellenor
Rockson Chang
Chao Zhuang
Xiaoxian Liu
UG’s: Max Touzel, Ardavan Darabi, Nan Yang, Michael Sitwell, Eugen Friesen
Some helpful theorists:
Atoms: Jalani Fox (Imperial)
QuickTime™ and a TIFF (Uncompressed) decompressor are needed to see this picture.
Pete Turner, Michael Spanner, Howard Wiseman, János Bergou, Masoud Mohseni, John Sipe, Paul Brumer,
...
Quantum Computer Scientists
The 3 quantum computer scientists:
see nothing (must avoid "collapse"!)
hear nothing (same story)
say nothing (if any one admits this thing
is never going to work,
that's the end of our
funding!)
OUTLINE
Measurement may mean many different things....
• {Forget about projection / von Neumann}
• Bayes’s Thm approach to weak values
• Thoughts on tunnelling
• 3-box problem
• joint weak values
• Retrodiction paradoxes
• Welcher Weg controversies
• Using measurements for good rather than for evil (à la KLM)
• Tomography in the presence of inaccessible information
• The Wigner function of the triphoton
Can we talk about what goes on behind closed doors?
(“Postselection” is the big new buzzword in QIP...
but how should one describe post-selected states?)
Conditional measurements
(Aharonov, Albert, and Vaidman)
AAV, PRL 60, 1351 ('88)
Prepare a particle in |i> …try to "measure" some observable A…
postselect the particle to be in |f>
i i
Measurement
of A
f f
Does <A> depend more on i or f, or equally on both?
Clever answer: both, as Schrödinger time-reversible.
Conventional answer: i, because of collapse.
Reconciliation: measure A "weakly."
Poor resolution, but little disturbance.
Aw
f Ai
f i
…. can be quite odd …
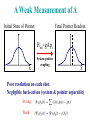
A (von Neumann) Quantum
Measurement of A
Initial State of Pointer
Final Pointer Readout
Hint=gApx
System-pointer
coupling
x
x
Well-resolved states
System and pointer become entangled
Decoherence / "collapse"
Large back-action
A Weak Measurement of A
Initial State of Pointer
Final Pointer Readout
Hint=gApx
x
System-pointer
coupling
x
Poor resolution on each shot.
Negligible back-action (system & pointer separable)
Strong:
Weak:
Bayesian Approach to Weak Values
Aw
f Ai
f i
Note: this is the same result you get from actually
performing the QM calculation (see A&V).
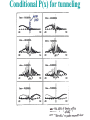
Weak measurement & tunneling
times
Conditional probability distributions
Conditional P(x) for tunneling
What does this mean practically?
QuickTime™ and a TIFF (Uncompressed) decompressor are needed to see this picture.
How many ways are there to be in
two places at one time?
We all know even a quantum particle may
not affect particles at spacelike separations.
But even a classical cause may have two
effects which are spacelike from each other.
On the other hand, a classical particle may
not have such effects.
Neither would a single photon split into two
paths of an interferometer.
If, from an ensemble of particles, each
affects only one region of spacetime, then the
difference between the two will grow noisier.
Perhaps the nonlocality of a tunneling particle is something deeper?
AMS, in Causality and Locality in Modern Physics (Kluwer: 1998); quant-ph/9710046
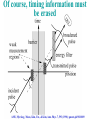
Of course, timing information must
be erased
AMS, Myrskog, Moon, Kim, Fox, & Kim, Ann. Phys. 7, 593 (1998); quant-ph/9810009
2
Quantum Let’s Make a Deal
Predicting the past...
A+B
B+C
What are the odds that the particle
was in a given box (e.g., box B)?
It had to be in B, with 100% certainty.
Consider some redefinitions...
In QM, there's no difference between a box and any other state
(e.g., a superposition of boxes).
What if A is really X + Y and C is really X - Y?
A+B
= X+B+Y
X
Y
B+C=
X+B-Y
A redefinition of the redefinition...
So: the very same logic leads us to conclude the
particle was definitely in box X.
X + B'
= X+B+Y
X
Y
X + C' =
X+B-Y
A Gedankenexperiment...
ee-
e-
e-
The 3-box problem: weak msmts
Prepare a particle in a symmetric superposition of
three boxes: A+B+C.
Look to find it in this other superposition:
A+B-C.
Ask: between preparation and detection, what was
the probability that it was in A? B? C?
Aw
f Ai
f i
PA = < |A><A| >wk = (1/3) / (1/3) = 1
PB = < |B><B| >wk = (1/3) / (1/3) = 1
PC = < |C><C|>wk = (-1/3) / (1/3) = -1.
Questions:
were these postselected particles really all in A and all in B?
can this negative "weak probability" be observed?
[Aharonov & Vaidman, J. Phys. A 24, 2315 ('91)]
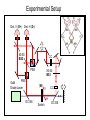
The implementation –
A 3-path interferometer
(Resch et al., Phys Lett A 324, 125('04))
Diode Laser
Spatial Filter: 25um PH, a 5cm and a 1” lens
l/2
GP A
BS1, PBS
l/2
MS, fA
GP B
BS2, PBS
GP C
BS4,
50/50
MS, fC l/2
BS3, 50/50
PD
CCD
Camera
Screen
The pointer...
• Use transverse position of each photon as pointer
• Weak measurements can be performed by tilting a
glass optical flat, where effective
Hint g A A p x
Mode A
q
Flat
gt
cf. Ritchie et al., PRL 68, 1107 ('91).
The position of each photon is uncertain to within the beam waist...
a small shift does not provide any photon with distinguishing info.
But after many photons arrive, the shift of the beam may be measured.
A negative weak value for Prob(C)
Intensity (arbitrary units)
Perform weak msmt
on rail C.
Post-select either A,
B, C, or A+B–C.
Compare "pointer
states" (vertical
profiles).
1.4
1.2
A+B–C
(neg. shift!)
Rail C
(pos. shift)
1
0.8
0.6
Rails A and B (no shift)
0.4
220
200
180
160
140
Pixel Number
K.J. Resch, J.S. Lundeen, and A.M. Steinberg, Phys. Lett. A 324, 125 (2004).
120
100
Post-selected state displacement
(Units of RMS Width)
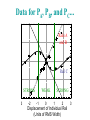
Data for PA, PB, and PC...
2
Rails A
and B
1
0
Rail C
-1
WEAK
STRONG
STRONG
-2
-3
-2
-1
0
1
2
Displacement of Individual Rail
(Units of RMS Width)
3
Is the particle "really" in
2 places at once?
• If PA and PB are both 1, what is PAB?
• For AAV’s approach, one would need an
interaction of the form
Hint g A A B B p x
OR: STUDY CORRELATIONS OF PA & PB...
- if PA and PB always move together, then
the uncertainty in their difference never changes.
- if PA and PB both move, but never together,
then D(PA - PB) must increase.
Practical Measurement of PAB
Resch &Steinberg, PRL 92,130402 ('04)
Use two pointers (the two transverse directions)
and couple to both A and B; then use their
correlations to draw conclusions about PAB.
Hint g A A A p x g B B B p y
We have shown that the real part of PABW
can be extracted from such correlation
measurements:
Re PABW
2 xy
g Ag Bt
2
- Re(P
*
AW
BBW )
Non-repeatable data which happen
to look the way we want them to...
anticorrelated
particle model
exact calculation
no correlations
(PAB = 1)
The joint probabilities
And a final note...
The result should have been obvious...
|A><A| |B><B|
= |A><A|B><B|
is identically zero because
A and B are orthogonal.
Even in a weak-measurement sense, a particle
can never be found in two orthogonal states at
the same time.
(So much for “serious” nonlocality of a tunneling
particle as well...)
3
“Quantum Seeing in the Dark”
" Quantum seeing in the dark "
(AKA: “Interaction-free” measurement,
aka “Vaidman’s bomb”)
A. Elitzur, and L. Vaidman, Found. Phys. 23, 987 (1993)
P.G. Kwiat, H. Weinfurter, and A. Zeilinger, Sci. Am. (Nov., 1996)
Problem:
D
C
Consider a collection of bombs so sensitive that
a collision with any single particle (photon, electron, etc.)
Bomb absent:
is guarranteed to trigger it.
Only detector C fires
BS2 that certain of
Suppose
the bombs are defective,
but differ in their behaviour in no way other than that
Bomb present:
they will not blow up when triggered.
"boom!"
1/2 bombs (or
Is there any way to identify
the working
C up? 1/4
some of them)
without blowing them
BS1
D
1/4
The bomb must be there... yet
my photon never interacted with it.
Hardy's Paradox
(for Elitzur-Vaidman “interaction-free measurements”)
C+
D+
D-
CD+
Outcome
–> e- was
Prob
in
Din
D+–>
ande+
C-was
1/16
BS2+
BS2I+
I-
O-
O+
W
BS1+
e+
BS1e-
D- and C+ 1/16
D+D- –> ?
C+ and C- 9/16
But
D+ …
and
if they
D- 1/16
were
both
in, they 4/16
Explosion
should
have annihilated!
The two-photon switch...
OR: Is SPDC really the time-reverse of SHG?
(And if so, then why doesn't it exist in classical e&m?)
The probability of 2 photons upconverting in a typical
nonlinear crystal is roughly 10-10 (as is the probability
of 1 photon spontaneously down-converting).
Quantum Interference
Suppression/Enhancement
of Spontaneous Down-Conversion
(57% visibility)
Experimental Setup
Det. V (D+) Det. H (D-)
50-50
BS2
CC
PBS
PBS
GaN
Diode Laser
DC BS
50-50
BS1
(W)
CC
V
H
Switch
DC BS
Using a “photon switch” to
implement Hardy’s Paradox
H Pol DC
V Pol DC
407 nm Pump
But what can we say about where the particles
were or weren't, once D+ & D– fire?
Probabilities e- in
e- out
e+ in
0
1
1
e+ out
1
-1
0
1
0
In fact, this is precisely what Aharonov et al.’s weak measurement
formalism predicts for any sufficiently gentle attempt to “observe”
these probabilities...
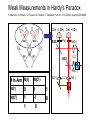
Weak Measurements in Hardy’s Paradox
Y. Aharonov, A. Botero, S. Popescu, B. Reznik, J. Tollaksen, PLA 301, 130 (2002); quant-ph/0104062
Det. V (D+) Det. H (D-)
BS2+
Pol.
BS2-
N(O+)
l/2
N(O-)
N(I+)
# In Arm
N(I-)
N(O-)
N(I+)
0
1
1
N(O+)
1
-1
0
1
0
l/2
N(I-)
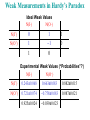
Weak Measurements in Hardy’s Paradox
Ideal Weak Values
N(I-)
N(O-)
N(I+)
N(O+)
0
1
1
1
-1
0
1
0
Experimental Weak Values (“Probabilities”?)
N(I-)
N(O-)
N(I+)
0.243±0.068
0.663±0.083
0.882±0.015
N(O+)
0.721±0.074
-0.758±0.083
0.087±0.021
0.925±0.024
-0.039±0.023
4
The Bohr-Einstein (and Scully-Walls) Debates...
Which-path controversy
(Scully, Englert, Walther vs the world?)
[Reza Mir et al., submitted to {everywhere} – work with H. Wiseman]
Which-path measurements destroy interference.
This is usually explained via measurement backaction & HUP.
Suppose we use a microscopic pointer.
Is this really irreversible, as Bohr would have all measurements?
Need it disturb momentum?
Which is «more fundamental» – uncertainty or complementarity?
Which-path measurements destroy
interference (modify p-distrib!)
• The momentum distribution clearly changes
• Scully et al prove there is no momentum kick
• Walls et al prove there must be some Dp > h/a.
• Obviously, different measurements and/or definitions.
• Is it possible to directly measure the momentum transfer?
(for two-slit wavefunctions, not for momentum eigenstates!)
Weak measurements
to the rescue!
To find the probability of a given momentum transfer,
measure the weak probability of each possible initial
momentum, conditioned on the final momentum
observed at the screen...
Wiseman, PLA 311, 285 (2003)
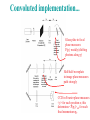
Convoluted implementation...
Glass plate in focal
plane measures
P(pi) weakly (shifting
photons along y)
Half-half-waveplate
in image plane measures
path strongly
CCD in Fourier plane measures
<y> for each position x; this
determines <P(pi)>wk for each
final momentum pf.
A few distributions P(pi | pf)
EXPERIMENT
THEORY
(finite width due to finite
width of measuring plate)
Note: not delta-functions; i.e., momentum may have changed.
Of course, these "probabilities" aren't always positive, etc etc...
The distribution of the integrated
momentum-transfer
EXPERIMENT
Note: the distribution
extends well beyond h/d.
On the other hand, all its moments
are (at least in theory, so far) 0.
THEORY
The former fact agrees with Walls
et al; the latter with Scully et al.
For weak distributions, they may
be reconciled because the distributions may take negative values in
weak measurement.
5
Measurement as a tool:
Post-selective operations for the construction of
novel (and possibly useful) entangled states...
Highly number-entangled states
("low-noon" experiment).
M.W. Mitchell et al., Nature 429, 161 (2004)
States such as |n,0> + |0,n> ("noon" states) have been proposed for
high-resolution interferometry – related to "spin-squeezed" states.
Important factorisation:
+
=
A "noon" state
A really odd beast: one 0o photon,
one 120o photon, and one 240o photon...
but of course, you can't tell them apart...
Theory: H. Lee et al., Phys. Rev. A 65, 030101 (2002); J. Fiurásek, Phys. Rev. A 65, 053818 (2002)
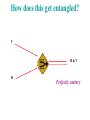
How does this get entangled?
H
2H
H
Non-unitary
How does this get entangled?
V
H&V
H
Perfectly unitary
How does this get entangled?
60˚
H & 60˚
H
Non-unitary
(Initial states orthogonal
due to spatial mode; final
states non-orthogonal.)
Trick #1
How to combine three non-orthogonal photons into one spatial mode?
"mode-mashing"
Yes, it's that easy! If you see three photons
out one port, then they all went out that port.
Post-selective nonlinearity
But do you really need non-unitarity?
V
H
PBS
Has this unitary, linear-optics, operation entangled the photons?
• Is |HV> = |+ +> - |– –> an entangled state of two photons at all,
or “merely” an entangled state of two field modes?
• Can the two indistinguishable photons be considered individual systems?
• To the extent that they can, does bosonic symmetrization mean that
they were always entangled to begin with?
Is there any qualitative difference in the case of N>2 photons?
Where does the weirdness come from?
HHH+VVV
C
(not entangled by
some definition)
B
A
If a photon winds up in each of modes {A,B,C}, then the three resulting
photons are in a GHZ state – 3 clearly entangled subsystems.
You may claim that no entanglement was created by the BS’s and postselection which created the 3003 state... but then must admit that some is
created by the BS’s & postselection which split it apart.
Trick #2
Okay, we don't even have single-photon sources*.
But we can produce pairs of photons in down-conversion, and
very weak coherent states from a laser, such that if we detect
three photons, we can be pretty sure we got only one from the
laser and only two from the down-conversion...
SPDC
|0> + e |2> + O(e2)
laser
* But
|0> + |1> + O(2)
e |3> + O(3) + O(e2)
+ terms with <3 photons
we’re working on it (collab. with Rich Mirin’s quantum-dot group at NIST)
Trick #3
But how do you get the two down-converted photons to be at 120o to each other?
More post-selected (non-unitary) operations: if a 45o photon gets through a
polarizer, it's no longer at 45o. If it gets through a partial polarizer, it could be
anywhere...
(or nothing)
(or nothing)
(or <2 photons)
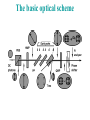
The basic optical scheme
It works!
Singles:
Coincidences:
Triple
coincidences:
Triples (bg
subtracted):
6
4b
Complete characterisation
when you have incomplete information
Fundamentally Indistinguishable
vs.
Experimentally Indistinguishable
But what if when we combine our photons,
there is some residual distinguishing information:
some (fs) time difference, some small spectral
difference, some chirp, ...?
This will clearly degrade the state – but how do
we characterize this if all we can measure is
polarisation?
Quantum State Tomography
Indistinguishable
Photon Hilbert Space
2
H
,0V , 1H ,1V , 0 H ,2V
HH
, HV VH , VV
?
Distinguishable Photon
Hilbert Space
H1H 2 , V1H 2 , H1V2 , V1V2
Yu. I. Bogdanov, et al
Phys. Rev. Lett. 93, 230503 (2004)
If we’re not sure whether or not the particles are distinguishable,
do we work in 3-dimensional or 4-dimensional Hilbert space?
If the latter, can we make all the necessary measurements, given
that we don’t know how to tell the particles apart ?
The Partial Density Matrix
The answer: there are only 10 linearly independent parameters which
are invariant under permutations of the particles. One example:
HH, HH
HV VH, HH
HH, HV VH HV VH, HV VH
HH,VV
HV VH,VV
Inaccessible
VV , HH
VV , HV VH
VV ,VV
information
HV -VH, HV -VH
Inaccessible
information
The sections of the density matrix labelled “inaccessible” correspond to
information about the ordering of photons with respect to inaccessible
degrees of freedom.
For n photons, the # of parameters scales as n3, rather than 4n
Note: for 3 photons, there are 4 extra parameters – one more
than just the 3 pairwise HOM visibilities.
A polarization measurement scheme
N.B.: You could imagine different schemes – e.g., a beam-splitter network
followed by independent polarizers – but you get no new information.
Experimental Results
R.B.A. Adamson, L.K. Shalm, M.W. Mitchell, AMS, PRL 98, 043601 (2007)
No Distinguishing Info
Distinguishing Info
When distinguishing
information is introduced the
HV-VH component increases
without affecting the state in
the symmetric space
HH + VV
Mixture of
45–45 and –4545
More Photons…
If you have a collection of spins, what
are the permutation-blind observables
that describe the system?
(* )
They correspond to measurements
of angular momentum operators
J and mj ... for N photons, J runs to N/2
So the total number of operators accessible to measurement is
N /2
Number of ordering - blind ops 2 j 1 N 3N 2N 1 / 6
2
j
E.g.,
for# 3ofphotons,
you need
Total
projectors
4 N 20 msmt’s: 16 for “spin-3/2” and 4 for “spin-1/2”
Totalquestion:
# of projectors
symmetric between
states bounds
N 1 you can place on
Open
what is onto
the relationship
2
distinguishability from these 4 numbers and from the 3 pairwise singlet proj’s?
(*) - Group theoretic approach thanks to Pete Turner
R.B.A. Adamson, P.S. Turner, M.W. Mitchell, AMS, quant-ph/0612081
Hot off the presses (well, actually, not on them yet):
Density matrix of the triphoton
(80% of population in symmetric subspace)
Extension to n-particle systems: R.B.A. Adamson, P.S. Turner, M.W. Mitchell, AMS, quant-ph/0612081
7
4b
A better description than
density matrices?
Wigner distributions
on the Poincaré sphere ?
(Consider a purely symmetric state: N photons act like a single spin-N/2)
Any pure state of a spin-1/2 (or a photon) can be represented as a point
on the surface of the sphere – it is parametrized by a single amplitude and
a single relative phase.
This is the same as the description of a classical spin, or the polarisation
(Stokes parameters) of a classical light field.
Of course, only one basis yields a definite result, so a better description
would be some “uncertainty blob” about that classical point... for spin-1/2,
this uncertainty covers a hemisphere , while for higher spin it shrinks.
0.9
2
0.8
1.8
0.7
0.6
1.6
1.4
1.2
0.5
1
0.4
0.8
0.3
0.6
0.2
0.1
0.4
0.2
Wigner distributions
on the Poincaré sphere
[Following recipe of Dowling, Agarwal, & Schleich, PRA 49, 4101 (1993).]
{and cf. R.L. Stratonovich, JETP 31, 1012 (1956), I’m told}
Can such quasi-probability distributions over the “classical”
polarisation states provide more helpful descriptions of the
“state of the triphoton” than density matrices?
“Coherent state” = N identically polarized photons
0.9
0.8
0.8
0.7
0.6
0.7
0.5
0.6
0.4
0.5
0.3
0.4
0.2
0.3
0.2
0.1
0
0.1
0
-0.1
-0.2
“Spin-squeezed state” trades off
uncertainty in H/V projection for
more precision in phase angle.
Please to note: there is nothing inside the sphere!
Pure & mixed states are simply different distributions on the surface,
as with W(x,p).
Beyond 1 or 2 photons...
A 1-photon pure state may be represented by a point on the surface
of the Poincaré sphere, because there are only 2 real parameters.
squeezed state
3-noon
0.8
15-noon
0.6
0.8
0.7
0.4
0.6
0.5
0.2
0.4
0.3
0
0.2
0.1
-0.2
0
-0.4
-0.1
-0.2
3 photons:
2 photons:
6 parameters:
4 param’s:
Euler angles
Euler angles
+ squeezing (eccentricity) + squeezing (eccentricity)
+ orientation
+ orientation
+ more complicated stuff
-0.6
-0.8
QuickTime™ and a
YU V420 codec decompressor
are needed to see this pict ure.
Making more triphoton states...
E.g.,
HV(H+V) = (R + iL) (L + iR) (R+iL+L+iR)
R2+L2 (R+L) =
R3 + R2L + RL2 + L3
In HV basis, H2V + HV2 looks “number-squeezed”; in RL basis, phase-squeezed.
The Triphoton on the rack
(?)
Another perspective on the problem
The moral of the story
1. Post-selected systems often exhibit surprising behaviour which
can be probed using weak measurements.
2. These weak measurements may “resolve” various paradoxes...
admittedly while creating new ones (negative probability)!
3. Post-selection can also enable us to generate novel “interactions”
(KLM proposal for quantum computing), and for instance to
produce useful entangled states.
4. POVMs, or generalized quantum measurements, are in some
ways more powerful than textbook-style projectors
Calculated Wigner-Poincaré
function for a variety
of “triphoton states”:
5. A modified sort of tomography is possible on “practically
indistinguishable” particles
QuickTime™ and a
YU V420 codec decompressor
are needed to see this pict ure.