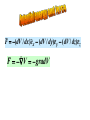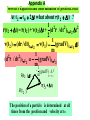Download No Slide Title

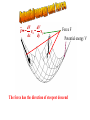
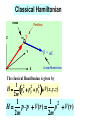
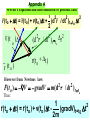
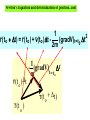
Welcome to the Chem 373
Sixth Edition
+ Lab Manual
It is all on the web !!
http://www.cobalt.chem.ucalgary.ca/ziegler/Lec.chm373/index.html
Lecture 1: Classical Mechanics and the Schrödinger Equation
This lecture covers the following parts of Atkins
1. Further information 4. Classical mechanics (pp
911- 914 )
2. 11.3 The Schrödinger Equation (pp 294)
Lecture-on-line
Introduction to Classical mechanics and the Schrödinger
equation (PowerPoint)
Introduction to Classical mechanics and the Schrödinger
equation (PDF)
Handout.Lecture1 (PDF)
Taylor Expansion (MS-WORD)
Tutorials on-line
The postulates of quantum mechanics (This is the writeup for
Dry-lab-II)( This lecture has covered (briefly) postulates
1-2)(You are not expected to understand
even postulates 1 and 2 fully after this lecture)
The Development of Classical Mechanics
Experimental Background for Quantum mecahnics
Early Development of Quantum mechanics
The Schrödinger Equation
The Time Independent Schrödinger Equation
Audio-Visuals on-line
Quantum mechanics as the foundation of Chemistry (quick time
movie ****, 6 MB)
Why Quantum Mechanics (quick time movie from the Wilson
page ****, 16 MB)
Why Quantum Mechanics (PowerPoint version without
animations)
Slides from the text book (From the CD included in
Atkins ,**)
QuickTime™ and a
Video decompressor
are needed to see this picture.
Classical Mechanics
A particle in 3 - D has the following attributes
1. Mass
mass
Z
Posit ion
m
m
2. Position r
velocit y
r
3. Velocity v
Y
v = dr /dt
X
Rate of change of position with time
Expression for total energy
The total energy of a particle with position r ,
mass m and velocity v also has energy
ET  Ekin  Epot (r )
Kinetic energy due
to motion
Potential energy
due to forces
Linear Momentum and Kinetic Energy
The kinetic energy can be written as :
1 2
Ek  mv
2
Or alternatively in terms of the
linear momentum:
p  mv
p
small mass large velocity
v
or
as:
2
p
Ek 
2m
v
large mass small velocity
The potential energy and force
A particle moving in a potential energy field V is subject to a
force
V(x)
Force in direction of
decreasing potential energy
F=-dV/dx
X
Force in one dimension
dV  dV


F
ex
ey
dx
dy
Force F
Potential energy V
The force has the direction of steepest descend
F  (dV / dx)ex  (dV / dy)e y  (dV / dz)ez
F  V  gradV
QuickTime™ and a
Video decompressor
are needed to see this picture.
QuickTime™ and a
Video decompressor
are needed to see this picture.
The Classical Hamiltonian
The expression for the total energy in terms of
the potential energy and the kinetic energy
given in terms of the linear momentum
p2
E  Ekin  Epot 
 V(r )
2m
is called the Hamiltonian
p2
H
 V(r )
2m
The Hamiltonian will take on a special
importance in the transformation from
classical physics to quantum mechanics
Quantum Mechanics
Classical Hamiltonian
We consider a particle of mass m,
and position r
Linear momentum p  mv
mass
Z
Position
m
r
Y
p = mv
X
Linear Momentum
The particle is moving in the potential V(x,y,z)
Classical Hamiltonian
mass
Z
Position
m
r
Y
p = mv
Linear Momentum
X
The classical Hamiltonian is given by


1
2
2
2
H
px  py  pz  V(x, y, z)
2m
1
1 2
H
p  p  V(r ) 
p  V(r )
2m
2m
Quantum Mechanical Hamiltonian
ˆ is constructed by the
The quantum mechanical Hamiltonian H
following transformations:


1
ˆ
HClass  H 
pˆ x2  pˆ 2y  pˆ z2  V( xˆ , yˆ , zˆ )
2m
Classical Mechanics Quantum Mechanics

x
px
xˆ   x ; pˆ x  
i x

y
py
yˆ   y ; pˆ y  
i y

z
pz
zˆ   z ; pˆ z  
i z
h
Here ' h - bar'=
is a modification of Plancks constant h
2
 1.05457  1034 Js
1
ˆ
H
( pˆ x2  pˆ 2y  pˆ z2 )  V( xˆ , yˆ , zˆ )
2m
1







[(

)(

)(

)]  V(x, y, z)
2m i x i x
i y i  y
i z i z
We have
2


 

 2
 
i y i y i y y
Thus
2

2
2
y
2
2
2



ˆ 
H
[ 2  2  2 ]  V(x, y,z)
2m x
y
z
2
2
2
2



ˆ 
H
[ 2  2  2 ]  V(x, y,z)
2m x
y
z
2
2
2
2



By introducing the Laplacian : 2  2  2  2 we have
x y z
ˆ 
H
 2  V(x, y, z)
2m
It is now a postulate of quantum mechanics that:
the solutions (x, y, z) to the Schrödinger equation
Hˆ (x, y, z)  E(x, y, z)

2
2m
 2 (r )  V(r )(r )  E(r )
2 2  2

[ 2  2  2 ]  V(x, y, z)  E
2m x
y
y
2
Contains all kinetic information about a particle
moving in the Potential V(x,y,z)
What you should learn from this lecture
Definition of :
Relation between force F
Linear momentum (pm),
p2
kinetic energy( );
2m
and potential energy V (F = -V)
Potential Energy
The definition of the Hamiltonian (H)
as the sum of kinetic and potential energy,
with the potential energy written in terms
of the linear momentum
p2
For single particle: H 
 V(r )
2m
ˆ
You must know that : The quantum mechanical Hamiltonian H
is constructed from the classical Hamiltonian H by
the transformation


1
ˆ
HClass  H 
pˆ x2  pˆ 2y  pˆ z2  V( xˆ , yˆ , zˆ )
2m
Classical Mechanics Quantum Mechanics
x
px
y
py
z
pz

xˆ   x ; pˆ x  
i x

yˆ   y ; pˆ y  
i y

zˆ   z ; pˆ z  
i z
Appendix A
Newton's Equation and determination of position..cont
The position of the particle is a function of time.
Let us assume that the particle at
has the position
and the velocity
What is
t  to
(d r / dt )t  tot
r (to )
v(t o )  (dr / dt)t to
r (t o )
(d 2 r / dt2 )t  to  t2
r(to  t)
r (to  t) = r (t1 ) = ?
By Taylor expansion around
r (to )
1 2
r (t o  t) = r (t o ) + (dr / dt) tt o t + (d r / dt 2 ) tt o t2
2
or
1 2
r (t o  t) = r (t o ) + v(to )t + (d r / dt 2 )t t o t2
2
Appendix A
Newton's Equation and determination of position..cont
1 2
r (t o  t) = r (t o ) + v(to )t + (d r / dt 2 )t t o t2
2
v (t o ) t
r (t o )
2

(d r / dt )t to t
2
2
r(t o   t)
However from Newtons law:
F(to )  V  gradV  m(d r / dt ) t t o
2
2
Thus :
1
2
r (t o  t) = r (t o ) + v(to )t (gradV)t=t 0 t
2m
Newton's Equation and determination of position..cont
1
2
r (t o  t) = r (t o ) + v(to )t (gradV)t=t 0 t
2m
v(t o ) t
r (t o )
1
- (gradV)t  t
= to
m
r (t o  t)
Appendix A
Newton's Equation and determination of position..cont
At the later time :
t1  to  t
we have
1 2
2
2
r(t1  t) = r(t1 ) + (dr / dt) t t1 t + (d r / dt )t t 1 t (1)
2
The last term on the right hand side of eq(1)
can again be determined from Newtons equation
F(t1 )  V  gradV  m(d2 r / dt 2 ) tt1
as
2
2
(d r / dt )t t1
1
  (gradV)t t1
m
Appendix A
Newton's Equation and determination of position..cont
1
2
r(t1  t) = r(t1 ) + (dr / dt) t t1 t +
(gradV)t t 1 t (1)
2m
We can determine the first term on the right side of
eq(1) By a Taylor expansion of the velocity
(dr / dt)t t 1  (dr / dt)t t 0
or
(dr / dt)t t 1
Where both:
1 2
 (d r / dt 2 )t t 0 t
2
1
 v(t o ) 
(gradV)t t o t
2m
v(t o )
1
(gradV)t to are known
and
m
Appendix A
Newton's Equation and determination of position..cont
At t 2  t0  2t what about r(t 2  t) ?
1 2
2
2
r(t 2  t) = r(t 2 ) + v(t 2 )t + (d r / dt ) t t 2 t
2
1
v(t 2 )  (dr / dt)t t 2  v(t 1 )  (gradV) tt 1 t
m
1
2
2
(d r / dt ) tt 2   (gradV)t t 2
m
v(t2 )  t
r (t 2 )
1
- (gradV)  t
m
t= t2
r(t2   t)
The position of a particle is determined at all
times from the position and velocity at to