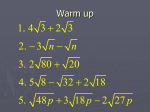Download MM212: Unit 8 Seminar

MM212: Unit 8 Seminar
•Solving equations by factoring.
•Simplifying radicals.
•Complex numbers.
Quadratic Equation
• A quadratic equation has this format
(standard form):
ax2 + bx + c = 0
• Where a, b, and c are real numbers, and a
cannot be 0
• in order for an equation to be considered
quadratic, there must be a squared term,
and 2 has to be the highest power
Solving by Factoring
1) Put the equation in standard form:
ax2+bx+c = 0
2) Factor the quadratic
3) Set each factor equal to zero
4) Solve each equation
5) Check your answer.
Example: x2+x=12
Solve by Factoring.
Put in standard form: x2+x-12=0
Factor: (x-3)(x+4) = 0
Set each factor equal to zero:
x-3 = 0 or x+4 = 0
Solve:
x = 3 or
x = -4
Check: 32+3-12 = 0 yes!
(-4)2+(-4)-12 = 16-4-12 = 0 yes!
Try this one:
2x2-9x = 5
Simplifying Radicals
 Based on what we saw in the nth root examples, we can see one of
the keys in simplifying radicals is to match the index and the
radicand’s exponent.
 A radical is considered simplified when:
 Each factor in the radicand is to a power less than the index of
the radical
 The radical contains NO fractions and NO negative numbers
NO radicals appear in the denominator of a
fraction
Properties of Radicals
• Product Rule for Radicals
n
n
n
 a* b
ab
n a * n b  n ab
Properties of Radicals
• Quotient Rule for Radicals
na
a
n
n
b
b
na
a
n

n
b
b
Simplifying Radicals
Factor the radicand
Group these factors in sets numbering the
same as the index
Use the Product Rule or Quotient Rule for
Radicals to rewrite the expression
Simplify (when the index and the radicands
exponent match, the radical simplifies as an
exponentless radicand)
Rationalizing Denominators
• Simplifying Radicals: A radical is considered simplified when:
 The radical contains NO fractions and NO negative numbers
 NO radicals appear in the denominator of a fraction
 The technique we use to get rid of any radicals in the
denominator of a fraction is called rationalizing.
 To rationalizing denominators, we are going to multiply the
denominator by something so that the index and the radicands
exponent match meaning the radical(s) in denominator will
simplify as an exponentless radicand.
Remember … if you multiply the denominator
times something, you must multiply the numerator
times the exact same thing!
CONJUGATES
(rationalizing denominators)
 These first four examples had only ONE term in the
denominator. If there are two terms, there is a slightly
different technique required in order to rationalize the
denominators.
We are going to multiply the denominator by
its CONJUGATE (Remember … if you
multiply the denominator times something,
you must multiply the numerator times the
exact same thing!)
§ 8.6
Complex Numbers
Imaginary Numbers
The equation x2 = – 4 does not have a real number solution. This
solution is an imaginary number.
The imaginary number i is defined as follows:
i  1 and i 2  1.
The set of imaginary numbers consists of numbers of the form bi,
where b is a real number and b  0.
For all positive real numbers a,
a  1 a  i a.
Imaginary Numbers
Example: Simplify.
a.)
b.)
49
49  1 49
27
27  1 27
 i(7)
i 9 3
 7i
 i(3) 3
 3i 3
Adding and Subtracting Complex
Numbers
For all real numbers a, b, c, and d,
(a + bi) + (c + di) = (a + c) + (b + d)i and
(a + bi)  (c + di) = (a  c) + (b  d)i.
Example: Subtract (7  2i)  (5  15i).
(7  2i)  (5  15i)  (7  2i)  (5  15i)
 (7  5)  (2  15)i
 2  17i
Multiplying Complex
Numbers
Example: Multiply (6  2i)(3 + i).
(6  2i)(3 + i) = (6)(3)  (6)i + (2i)(3) + (2i)(i)
= 18  6i  6i  2i 2
= 18  6i  6i  2(1)
= 18  2
= 20
FOIL.
Complex Numbers of the
n
Form i
Values of in
i=i
i5 = i
i9 = i
i = 1
i = 1
i = 1
i = i
i = i
i = i
i 4 = 1
i8 = 1
i12 = 1
2
6
3
7
Example: Evaluate i35.
i35 = (i5)7
= (i)7
=–i
10
11
Notice
the
pattern.
Dividing Complex Numbers
Example: Divide
6i
.
4 + 3i
6  i 4  3i
24  18i  4i  3i 2


4 + 3i 4  3i
16  9i 2
Conjugate
of 4 + 3i.

24  22i  3(1)
16  9(1)

24  22i  3
16 + 9

21  22i
21 22
or
 i
25
25 25