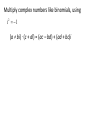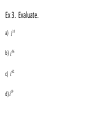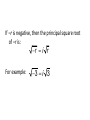Download Sec 3.4 & Sec 3.5 Complex Numbers & Complex Zeros

Sec 3.4 & Sec 3.5
Complex Numbers & Complex Zeros
Objectives:
•To understand complex numbers.
•To add, subtract & multiply complex
numbers.
•To solve equations with complex
numbers as solutions.
Complex Numbers
If i 2  1 , then i  1
A complex number is a number of the form
a  bi where a and b are real numbers.
The real part of the complex number is a and
the imaginary part is bi.
Ex 1. State the real and imaginary
parts of the following complex
numbers.
a) 7 + 3i
b) 9i
c) -2
Operations on Complex Numbers
To add complex numbers, add the real parts and
add the imaginary parts.
(a + bi) + (c + di) = (a + c) + (b + d)I
To subtract complex numbers, subtract the real
parts and subtract the imaginary parts.
(a + bi) – (c + di) = (a – c) + (b – d)i
Multiply complex numbers like binomials, using
i 2  1
(a + bi) . (c + di) = (ac – bd) + (ad + bc)i
Ex 2. Perform the indicated operation
and write the result as a + bi.
(a) (3 + 5i) + (4 – 2i)
(b) (3 + 5i) – (4 – 2i)
(c) (3 + 5i)(4 – 2i)
Powers of i
Any power of i can be reduced to one of the
following:
i i
1
i  1
2
i  i
3
i 1
4
To reduce a power of i, just
divide by 4 and the remainder
will correspond to one of
23
these. For example, i  i
Because 23/4 has a remainder
of 3 so the answer corresponds
3
to i
Ex 3. Evaluate.
a) i 35
b) i 56
c) i 62
d) i
19
Class Work
Perform the indicated operation and write your
answer in a + bi form.
1. (2 + 5i) + (4 – 6i)
2. (5 – 3i)(1 + i)
3. i 43
Square Roots of Negative Numbers
Just as every positive real number r has two
square roots  r and  r  , every negative
number has two square roots as well.
If -r is a negative number, then its square roots are
i r , because:
 
 i 2r  r


i r
and
2
i r
2
 i 2r  r
If –r is negative, then the principal square root
of –r is:
r  i r
For example:
3  i 3
Ex 4. Evaluate the expression.
 a  1 
 b  16 
 c  7 
Ex 5. Evaluate and write the result in
the form of a + bi.


12  3 3  4

Class Work
Evaluate the expression and write your result in
the form of a + bi.
4. 32
5. 25
6.
3 12
7.

3  4

6  8

Complex Roots of Quadratic Equations
We know that if b2 – 4ac < 0 then the quadratic
has no real solutions. However, in the
complex number system, the equation will
always have solutions. The solutions will be
complex numbers and will have the form
a + bi and a – bi. The solutions will always
come in pairs, called conjugates.
Ex 6. Solve each equation.
(a) x2 + 9 = 0
(b) x2 + 4x + 5 = 0
Class Work
Find all the zeros of the polynomial.
8. P( x)  x3  x 2  x
9. P( x)  x  7 x  18x  18; x  3
3
2
4
2
P
(
x
)

x

x
 2 x  2; x  1, 1
10.
Ex 7. Find a polynomial with
integer coefficients that have the
given zeros.
a) Degree 3 and zeros 2 and i.
b) Degree 2 and zeros 1 + i, and 1 – i.
HW Worksheet 3.4 & 3.5