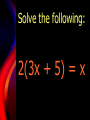Download Chapter 7 - pantherFILE

Algebraic Structures:
An Activities Based Course
MATH 276
UWM
The Handshake Problem
 There are 32 people in this room.
 If everyone shakes hands with
everyone else in the room, how
many handshakes will there be?
Please write the following:
 Name
 Phone number
 E-mail address
 School
 Subjects/Grade level you
teach
 Something you would like me
to know
What is a Number?
How do we use
numbers?
How do we use numbers?
 Count
 Order
 Compare
 Measure
 Summarize
 Locate
 Identify
 Operate with
numbers
 Collect numbers;
put them into sets
 Identify/describe
patterns
 Follow rules
Win-a-Row
 Game for 2 people: one positive, one
negative
 Each player has 8 numbers. 4 x 4 game
board
 Decide who goes first.
 In turn, write one of your numbers on the
game board. A number may be used only
once.
 Add each row and columns. Write the
sums. If more sums are +, + wins.
 After you have played a few games, write
addition patterns you see.
Solve the following:
2(3x + 5) = x
Integral Domain - pg. 146
(Z, +, ·)
 The integral domain of integers is the
set:
Z = {. . ., -3, -2, -1, 0, 1, 2, 3, …}
together with the operations of ordinary
addition and multiplication which satisfy
properties.
Principle of Well-Ordering
Every non-empty
subset of N+
contains a
smallest element.
The Handshake Problem
 There are 32 people in this room.
 If everyone shakes hands with
everyone else in the room, how
many handshakes will there be?
Carl Friedrich Gauss
QuickTime™ and a
TIFF (Uncompressed) decompressor
are needed to see this picture.
1777 - 1855
1 + 2 + 3 + 4 + 5 + . . . 100
Proof by Induction
Quic kTime™ and a
TIFF (Unc ompres sed) dec ompres sor
are needed to see t his pic ture.
• The first domino falls.
• If the k domino falls, the k + 1 domino will fall.
If this number is written in
standard place value form,
what digit appears in the
unit’s place?
2009
2009
 Think of a number.
 Add seven.
 Multiply by two.
 Subtract four.
 Divide by two.
 Subtract the first number
you thought of.
When is the Inductive
Method of Proof helpful?
 You can start with a conjecture.
 You want to prove the conjecture
for a set with a smallest element.
 Inductive proofs are often used
for sequence of partial sum
patterns.
1 + 2 + 4 + 8 + . .+ 2k-1 = 2k - 1
Inductive proof
Prove
the
conjecture
is
true
for the smallest element in
the set.
Prove:
If
the
conjecture
is
true for n = k, then it is true
for n = k + 1.
What is the smallest
number evenly divisible by
1, 2, 3, 4, 5, 6, 7, 8, 9, 10?
Prime Numbers and the
Sieve of Eratosthenes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Prime Number
 An integer n > 1 is prime if its only
positive divisors are 1 and itself.
 An integer n > 1 that is not prime is
called composite.
 A prime factorization of a positive integer
n is an expression of the form:
n = p1 · P2 · p3 · · · pk
Fundamental Theorem
of Arithmetic
Every positive integer
other than 1 can be
factored into prime factors
in exactly one way, except
possibly for the order of
factors.
Divisors and Multiples
a|b
True or False?











3|9
12|6
0|5
11|11
If a|b and b|c, then a|c
5|6!
11|6!
If c|a and c|b, then c|(a + b)
If c|a and c|b, then c|(a - b)
8|(8! + 1)
6|(6! - 3!)
Quic kTime™ and a
TIFF (Unc ompres sed) dec ompres sor
are needed to see t his pic ture.
Ferris Wheel Problem
 You and your sister go to a carnival that has both a large
and a small Ferris wheel.
 You begin your ride on the large one at the same time your
sister begins to ride the small one. Determine the number
of seconds that will pass before you and your sister are both
at the bottom again.
 A. The large makes one revolution in 60 seconds and the
small makes a revolution in 20 seconds.
 B. The large makes one revolution in 50 seconds and the
small makes a revolution in 30 seconds.
 C. The large makes one revolution in 12 seconds and the
small makes a revolution in 9 seconds.
Quic kTime™ and a
TIFF (Unc ompres sed) dec ompres sor
are needed to see t his pic ture.
Factor Patterns
 5! = 5 • 4 • 3 • 2 • 1 = 120
 6! = 6 • 5 • 4 • 3 • 2 • 1 = 720
 10! = 10 • 9 • 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1
= 33,628,800
 Note that 5! And 6! both end in one zero, and
10! ends in two zeros. Without computing 50!,
determine the number of zeros in which 50!
ends. (50! ≠ 5! • 10!)
Measuring with Index Cards
 Draw as many segments as possible,
each with a different length, measuring
1 inch, 2 inches, 3 inches, . . . up to 10
inches using:
a. only a 3 x 5 inch index card
b. only a 4 x 6 inch index card.
The Division Algorithm
Pg. 154
 b = aq + r 0 < r < a
 aq < b < a(q + 1)
Euclidean Algorithm
 Use the Euclidean algorithm to find
gcd (15,70)
 Use the Euclidean Algorithm to find
gcd (276,588)
Factor Patterns
 5! = 5 • 4 • 3 • 2 • 1 = 120
 6! = 6 • 5 • 4 • 3 • 2 • 1 = 720
 10! = 10 • 9 • 8 • 7 • 6 • 5 • 4 • 3 • 2 • 1
= 33,628,800
 Note that 5! And 6! both end in one zero,
and 10! ends in two zeros. Without
computing 25!, determine the number of
zeros in which 25! ends. (25! ≠ 5! • 5!)
Summary














Algebraic Structures
Sets of Numbers, Integers, N+ (Natural Numbers)
Properties of Integers,
Real Number System (R, +, •)
Definitions
Inductive Proof
Prime Numbers; Composite Numbers
Fundamental Theorem of Arithmetic
a|b and properties
Divisors (factors), Find gcd ( )
Multiples, Find lcm ( )
The product a•b = gcd (a,b) • lcm (a,b)
Division Algorithm
Euclidean Algorithm
Presentations
 Teach Euclidean Algorithm
 Prove the square root of 2 is an irrational
number.
 7.12, pg. 152
 7.13, pg. 152 with proof
 Option (7.3, 7.4, 7.5 Tower of Hanoi)
 Teach a lesson: The Locker Problem, Crossing
the River, Cuisenaire Trains
 Each a lesson on Abundant, Deficient, Perfect
Numbers
Even and Odd Numbers
Write a definition for:
even number
Write a definition for:
odd number
Rational and Irrational
Numbers
 The need for multiplicative
inverses and rational numbers
 The need for irrational numbers
 Prove √ 2 is an irrational number.
(Pg. 159)
 Real Numbers - Filling the holes
on the number line
 Complex Numbers - A solution
for x2 + 1 = 0; √-1 = i
Proof by Contradiction or
Indirect Proof
 You are taking a true-false quiz with 5
questions.
 From past experience you know:
If the first answer is true, the next one is
false.
The last answer is always the same as the
first answer.
You are positive the second answer is true.
On the assumption that these statements are
correct, prove that the last answer is false.
Locker Problem
 http://connectedmath.msu.edu/CD/Grade
6/Locker/index.html
Mental Math Problems
 1) 12 x 15
 6) 3 x 36
 2) 9 x 15
 7) 16 x 14
 3) 90 x 14
 8) 7 x 25
 4) 2 x 18
 9) 2 x 5 x 0 x 7
 5) 12 x 9
 10) 12 x 1 x 11
Using the Graphing Calculator
Rule ( X KEY, Y = )
Table ( TBLSET, TABLE )
Graph ( WINDOW, TRACE,
MODE, FORMAT )