* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download 2 Better Maths Teaching at KS2
Survey
Document related concepts
Transcript
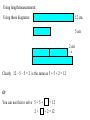
Principles of Good Maths Teaching Objectives: •Understand the essence of ‘Good Maths Teaching’ •Look at some activities that encourage ‘Good Maths Teaching’ •Look at important skills necessary to make progress after KS2: Specifically look at resources and issues around a) Fractions b) Inverse Operations c) Proportional Reasoning Maths Activity A – 5 minutes 1 2 3 4 5 6 7 8 9 10 Number counters 1 to 10. Use pairs to make 10 Which numbers are left over? Why? What if you had to make a total of 11? 12? 13? 14? Principle 1: Pupils understand maths when they are using and doing maths. The trick is to set up situations where the pupils can use maths in open ended ways. Fewer closed questions and more open questions that let them explore their own reasoning. Good maths teaching is about developing understanding Maths Activity B – 5 minutes Either: Write down 3 different numbers that sum to be 12? How many ways can you do this? Or: Twelve can be written as the sum of 3 consecutive numbers. What are they? Can you find 5 more numbers that can be written as the sum of 3 consecutive numbers? Can you find 5 numbers that can be written as the sum of 5 consecutive numbers? Can you find 5 numbers that can be written as the sum of 5 consecutive numbers and 3 consecutive numbers? Principle 2: Start at 10 and count back to -10 How many numbers did you say? Principle 2: Start at 10 and count back to -10 How many numbers did you say? We use numbers for two purposes: 1) To count 2) To measure Often we spend too much time focusing on counting rather than measuring. Measuring is more intuitive and more kinaesthetic/visual. It is an underused tool in developing number sense. Maths Activity C – 5 minutes 0 10 20 30 40 50 0 1 2 3 4 5 What is 20 ÷ 10? What is 2 ÷ 1? What is 10 ÷ 5? What is 1 ÷ 0.5? How many divisions can you write down where the answer is 2? Principle 3: The Numeracy Strategy had a focus on mental methods. Excelling at mental maths requires many different tricks to get to the answers. BUT too many techniques can cause confusion with weaker students It is better to agree on a standard school method for adding, subtracting, multiplying and dividing and work towards developing it without getting distracted by other methods. Use ‘clever tricks’ or new methods only when pupils are secure in the main method. Maths Activity D – 5 minutes Blonde Hair Only 1 face. How many ways? What about 2? or 3? Most? Sad Making Rich Maths Tasks: Turning a Closed Question into an Open Question Closed: Open: Find the perimeter of these shapes. Can you find 6 items in the room with a Perimeter of between 20 cm and 50 cm? Closed: What is 14 divided by 6? Open: Closed: Open: What is 14 divided by 6? I think of a number. When I divide it by 6 I get a remainder of 2. What number might I have thought of? When I divide my number by 5 I get a remainder of 3. What number might I have thought of? Closed: Find the perimeter of these shapes/items. Open: Closed: Open: Find the perimeter of these shapes/items. Suppose you have 5 cm squares. How many different shapes can you make from them. Which shape has the largest perimeter? Which has the smallest perimeter? OR If you had 12 cm squares Find the shape(s) with the largest/smallest perimeter? Are you are answers unique? How do you know? Closed: What is the next number in this sequence: 2, 4, 6, 8, 10, …… Open: Closed: Open: What is the next number in this sequence: What is the next number in this sequence: 1, 3, …… 2, 4, 6, 8, 10, …… OR Write down 4 numbers in a sequence OR Here are some numbers. Give a reason why each of them might be the odd one out: 6, 15, 30, 40 Closed: Open: What is the next number in this sequence: Hand out a variety of 2d shapes – different colours, sizes, number of sides 2, 4, 6, 8, 10, …… Make a path with according to some rule: Eg: red, blue, yellow, red, blue yellow, red blue yellow, Or 3 sides 4, sides 3, sides, 4 sides Or Triangle, square, triangle square, Or Triangle, square, pentagon, hexagon, Describe your pattern to someone else? Can they add another shape in Closed: Construct a bar chart for 3 red cars and 5 blue cars Open: Closed: Open: Construct a bar chart for 3 red cars and 5 blue cars What is this a graph of: Closed: What is the product of 8 and 16? Open: Closed: Open: What is the product of 8 and 16? The product of two whole numbers is 128. What were the two numbers? How many possibilities? Closed: Open: Find the missing number: 8+ = 15 Closed: Open: Find the missing number: How many pairs of numbers can you find that sum to 15 8+ = 15 OR + = 15 Closed: What shape is this? Open: Closed: Open: What shape is this? Draw as many different shapes as you can in the next 5 minutes Or Hand out a loop of string – what shapes can you make? Get pupils into pairs what shapes can they make? Suppose you had groups of 3 and each child pulled on the string to make it taut – what shape would you make? Would every group make the same shape? What if you had groups of 4? Maths Activity E – 5 minutes I arrange the pupils in KS2 into rows with an equal number in each row. When I have rows of 3 I have one pupil left over. When I have rows of 4 I have one pupil left over. When I have rows of 5 I have one pupil left over. When I have rows of 6 I have one pupil left over. How many pupils in KS2? Is there only one answer? Important Skills Required to Bridge the Gap from KS2 to KS3 1) Being able to add and subtract whole and decimal numbers Place value is key. Money is a good approach but also use length. Subtraction 12.8 – 1.43 always an issue 2) Recall of Multiplication tables Written method to multiply two digit whole numbers together Grid Method is a good approach that leads to more developed written techniques 3) Division Chunking leading to short division You can’t do division unless you know your times tables Remainders drive me nuts! Important Skills Required to Bridge the Gap from KS2 to KS3 4) Inverse Relationships That 5 + 6 = 11 is equivalent to 11 – 6 = 5 11 – 5 = 6 That 4 × 3 = 12 is equivalent to 12 ÷ 3 = 4 12 ÷ 4 = 3 5) Understanding what a fraction really represents Understand that 2/5 means two out of 5 equal parts for example Understand that the denominator is a label representing the number of equal parts in the whole. 6) Proportional Reasoning If 6 pints of mile costs me £2.40 how much will 7 pints of milk cost. Using the unitary method. Resources for helping with Number Work: Put the numbers 1 to 6 into the circles so that the circle resting on each pair is equal to the difference in their values Repeat with 10 circles and the numbers 1 to 10 Pick any three numbers between 1 and 9 to go in the bottom three circles. Each circle’s value is the product of the two numbers it is resting on. What is the biggest total you can make in the top circle? What is the smallest total? What is the largest odd total? Write down 3 consecutive numbers: Square the middle number and multiply the outside two. What is the difference in your answers? Repeat with a different set of 3 numbers ……. Write down 4 consecutive numbers. Find the difference in the product of the 1st and 4th and the 2nd and 3rd? What do you notice? Repeat with 5 numbers? 6 numbers? Strike it Out You need a friend to play with One of you draw a 0-20 number line like this 3 + 8 = 11 11 + 9 = 20 20 - 4 = 16 The answers to these three questions use 8 of the 9 digits in the grid. Which digit is not used? 13 x 19 = ? 4 5 8 14 x 7 = ? 1 2 1 119 + 32 = ? 7 9 1 Make up your own problem? Design your own grid. Can you find three questions to match a grid that has 9 different digits in it! Resources for helping with Inverse Relationships: Ergo Grids Using length/measurement: 12 cm Using these diagrams: 5 cm 2 cm Clearly 12 – 5 – 5 = 2 is the same as 5 + 5 + 2 = 12 Or You can use this to solve 5 + 5 + 2× = 12 + 2 = 12 Balancing Scales from Nrich: Suppose you have a number machine that always does the same thing. It is first set up to add 10. I put three numbers into the machine: The first number gives me 12 The second number gives me 15 The third number gives me 8 What numbers did I put in the machine. I then reset the machine so that it is doing a different add or take away and I put in 4 new numbers. One of the numbers that I put in the machine is the number 10. If the outputs are: 0 , 19, 1 and 11 What numbers did I put in the machine? Resources for addressing issues with fractions Pupils struggle to understand that the denominator doesn’t represent an amount but is really a label telling you how many parts the whole has been chopped into We often get pupils to colour in diagrams like: this to represent 3/4 . It is better to get them to do their own partitioning. What fraction of each shape is shaded? Draw a picture to show ½ + 1/4? Fractions need to used to describe as wide a range of situations as possible: Discrete wholes: Eg 3 red marbles and 5 blue Continuous wholes: Eg Cut this circle into thirds (measurements!) Definite wholes: What fraction of shapes are hearts? Indefinite wholes: Every Monday since I started work I have bought myself a kit-kat at lunch time. What fraction of days have I had a kit-kat for lunch? It is easy to get stuck on halving and (quartering halving a half…) Make certain that pupils are exposed to other fractions at an early age (thirds, fifths etc) Encourage the children to make meaningful comparisons E.g. ‘I invite 4 children to a part and order 3 pizzas’ Does every child get more or less than half a pizza? How much does each child receive? ‘What if I invited 8 children and ordered 6 pizzas’ would each child get more or less pizza? ‘If I invite 5 children and order 4 pizzas’ will each child get more or less pizza? = 1 whole? a) What fraction is b) What fraction is ? ? Resources for helping with Proportional Reasoning: Eg. If 6 pints of mile costs me £2.40 how much will 7 pints of milk cost. Using the unitary method with a diagram. 40 p 40 p 40 p 40 p 40 p 40 p To make 20 litres of orange paint you need 8 litres of red paint and 12 litres of yellow paint Red 8 Yellow 12 Total 20 10 40 16 60 200 9 18 75 Maths Activity F – 5 minutes You have a blank 100 square Where do these numbers go on this number grid? 1, 5, 13, 24, 45, 30, 75, 99 What if the grid was a 9 by 9 square? A hundred square has been printed on both sides of a piece of paper. One square is directly behind the other. What is on the back of 100? 58? 23? 19? Can you see a pattern? Maths Activity G – 5 minutes