* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 2 - Part 1 - PPT - Mano & Kime
Large numbers wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
List of first-order theories wikipedia , lookup
Approximations of π wikipedia , lookup
Elementary mathematics wikipedia , lookup
Location arithmetic wikipedia , lookup
Positional notation wikipedia , lookup
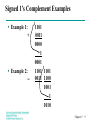
Logic and Computer Design Fundamentals Lecture 17: Signed Arithmetic Charles Kime & Thomas Kaminski © 2004 Pearson Education, Inc. Terms of Use (Hyperlinks are active in View Show mode) Overview Signed Integers • Sign-magnitude • Complement representations Binary adder-subtractors • Signed binary addition and subtraction Overflow Binary multiplication Other arithmetic functions • Design by contraction Chapter 5 2 Signed Integers Positive numbers and zero: • Use unsigned n-digit, radix r numbers Negative numbers: • Need a sign bit (+ or -) • By convention, the MSB is the sign bit: s an–2 a2a1a0 where: s = 0 for Positive numbers s = 1 for Negative numbers and ai = 0 or 1 represent the magnitude in some form. Chapter 5 3 Signed Integer Representations Signed-Magnitude – here the n – 1 digits are interpreted as a positive magnitude. Signed-Complement – here the digits are interpreted as the rest of the complement of the number. • Signed 1's Complement Uses 1's Complement Arithmetic • Signed 2's Complement Uses 2's Complement Arithmetic Chapter 5 4 Signed Integer Representation Example r =2, n=3 Number +3 +2 +1 +0 –0 –1 –2 –3 –4 Sign -Mag. 011 010 001 000 100 101 110 111 — 1's Comp. 011 010 001 000 111 110 101 100 — 2's Comp. 011 010 001 000 — 111 110 101 100 Chapter 5 5 Signed-Magnitude Arithmetic Algorithm is covered in the book Awkward • Complex rules for correction Not covered in detail • You are not expected to know this • You are expected to know that it is possible Instead, use complement-based representations • One’s complement • Two’s complement Chapter 5 6 Signed-Complement Arithmetic Addition: • Use conventional unsigned adder • Sign bit is produced correctly, except • Overflow can occur: If the sign bits were the same for both numbers and the sign of the result is different, an overflow has occurred. Subtraction: • Form the complement of the number you are subtracting and follow the rules for addition. Chapter 5 7 Signed 2’s Complement Examples Example 1: 1101 +0011 0000 Example 2: 1101 1101 -0011 1101 1010 Chapter 5 8 Signed 1’s Complement Examples Example 1: + Example 2: - 1 1101 0011 0000 1 0001 1 1101 1101 0011 1100 1001 1 1010 Chapter 5 9 2’s Complement Adder/Subtractor Subtraction can be done by addition of the 2's Complement. 1. Complement each bit (1's Complement.) 2. Add 1 to the result. The circuit shown computes A + B and A – B: For S = 1, subtract B3 • Invert B with XOR • Add 1 by setting C0 A3 B2 A2 B1 A1 B0 A0 S For S = 0, add, B is passed through unchanged FA C4 S3 C3 FA S2 C2 FA S1 C1 FA C0 S0 Chapter 5 10 Overflow Detection Overflow occurs if n + 1 bits are required to contain the result from an n-bit addition or subtraction Unsigned addition • 5 + 6 > 7: 101 + 110 => 1011 • Carry out from MSB indicates unsigned overflow Signed addition • 2 + 3 = 5 > 4: 010 + 011 = 101 =? –3 < 0 Sum of two positive numbers should not be negative • -1 + -4: 111 + 100 = 011 > 0 Sum of two negative numbers should not be positive SignedOverflow S n -1an -1bn -1 S n -1an -1bn -1 Chapter 5 11 Binary Multiplication The binary digit multiplication table is trivial: (a × b) b=0 b=1 a=0 0 0 a=1 0 1 This is simply the Boolean AND function. Form larger products the same way we form larger products in base 10. Chapter 5 12 Review - Decimal Example: (237 × 149)10 Partial products are: 237 × 9, 237 × 4, and 237 × 1 2 3 Note that the partial product × 1 4 summation for n digit, base 10 2 1 3 numbers requires adding up 9 4 8 to n digits (with carries). + 2 3 7 Note also n × m digit 3 5 3 1 multiply generates up to an m + n digit result. 7 9 3 3 Chapter 5 13 Binary Multiplication Algorithm We execute radix 2 multiplication by: • Computing partial products, and • Justifying and summing the partial products. (same as decimal) To compute partial products: • Multiply the row of multiplicand digits by each multiplier digit, one at a time. • With binary numbers, partial products are very simple! They are either: all zero (if the multiplier digit is zero), or the same as the multiplicand (if the multiplier digit is one). Chapter 5 14 Example: (101 x 011) Base 2 Partial products are: 101 × 1, 101 × 1, and 101 × 0 1 0 Note that the partial product × 0 1 summation for n digit, base 2 1 0 numbers requires adding up 1 0 1 to n digits (with carries) in 0 0 0 a column. 0 0 1 1 1 Note also n × m digit multiply generates up to an m + n digit result (same as decimal). 1 1 1 1 Chapter 5 15 Multiplier Boolean Equations An n × m “block” multiplier forms partial products. Example: 2 × 2 – The logic equations for each partial-product binary digit are shown below: We need to "add" the columns to get the product bits P0, P1, P2, and P3. b1 b0 a1 a0 Note that some . b1) (a0 . b0) (a 0 columns may + (a1 . b1) (a1 . b0) generate carries. P3 P2 P1 P0 Chapter 5 16 Multiplier Arrays Using Adders An implementation of the 2 × 2 A multiplier array is shown: 0 B1 B0 A1 B1 B0 HA HA C3 C2 C1 C0 Chapter 5 17 Other Arithmetic Functions Convenient to design the functional blocks by contraction - removal of redundancy from circuit to which input fixing has been applied Functions • Incrementing • Decrementing • Zero Fill and Extension Chapter 5 18 Design by Contraction Contraction is a technique for simplifying the logic in a functional block to implement a different function • The new function must be realizable from the original function by applying rudimentary functions to its inputs Contracted version specialized for a fixed input • Logic can be much simpler Chapter 5 19 Design by Contraction Example Contraction of a ripple carry adder to incrementer for n = 3 • Set B = 001 • The middle cell can be repeated to make an incrementer with n > 3. Chapter 5 20 Incrementing & Decrementing Incrementing • • • • Adding a fixed value to an arithmetic variable Fixed value is often 1, called counting (up) Examples: A + 1, B + 4 Functional block is called incrementer Decrementing • • • • Subtracting a fixed value from an arithmetic variable Fixed value is often 1, called counting (down) Examples: A - 1, B - 4 Functional block is called decrementer Chapter 5 21 Zero Fill Zero fill - filling an m-bit operand with 0s to become an n-bit operand with n > m Filling usually is applied to the MSB end of the operand, but can also be done on the LSB end Example: 11110101 filled to 16 bits • MSB end: 0000000011110101 • LSB end: 1111010100000000 Chapter 5 22 Sign Extension Sign Extension – maintaining sign bit for a complement representation • Copies the MSB of the operand into the new positions • Positive operand example - 01110101 extended to 16 bits: 0000000001110101 • Negative operand example - 11110101 extended to 16 bits: 1111111111110101 Results in equivalent number in a wider representation Chapter 5 23 Summary Signed Integers • Sign-magnitude • Complement representations Binary adder-subtractors • Signed binary addition and subtraction Overflow Binary multiplication Other arithmetic functions • Design by contraction Chapter 5 24 Terms of Use © 2004 by Pearson Education,Inc. All rights reserved. The following terms of use apply in addition to the standard Pearson Education Legal Notice. Permission is given to incorporate these materials into classroom presentations and handouts only to instructors adopting Logic and Computer Design Fundamentals as the course text. Permission is granted to the instructors adopting the book to post these materials on a protected website or protected ftp site in original or modified form. All other website or ftp postings, including those offering the materials for a fee, are prohibited. You may not remove or in any way alter this Terms of Use notice or any trademark, copyright, or other proprietary notice, including the copyright watermark on each slide. Return to Title Page Chapter 5 25