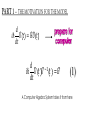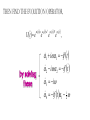* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Defense Presentation
Path integral formulation wikipedia , lookup
Hidden variable theory wikipedia , lookup
Probability amplitude wikipedia , lookup
Quantum state wikipedia , lookup
Density matrix wikipedia , lookup
Wave–particle duality wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Coherent states wikipedia , lookup
Lattice Boltzmann methods wikipedia , lookup
Particle in a box wikipedia , lookup
Quantum electrodynamics wikipedia , lookup
Ising model wikipedia , lookup
History of quantum field theory wikipedia , lookup
Tight binding wikipedia , lookup
Ferromagnetism wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Hydrogen atom wikipedia , lookup
Scalar field theory wikipedia , lookup
Atomic theory wikipedia , lookup
Rotational–vibrational spectroscopy wikipedia , lookup
Rutherford backscattering spectrometry wikipedia , lookup
Quantum group wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Franck–Condon principle wikipedia , lookup
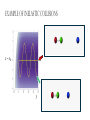
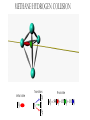
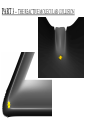
ALGEBRAIC SEMI-CLASSICAL MODEL FOR REACTION DYNAMICS Tim Wendler, PhD Defense Presentation TOPICS: Part 1 – Motivation Part 2 – The Dipole Field Model Part 3 – The Inelastic Molecular Collision Model Part 4 – The Reactive Molecular Collision Model PART 1 – THE MOTIVATION FOR THE MODEL 𝑑 𝑖ℏ 𝑈 𝑡 = 𝐻 𝑈 𝑡 𝑑𝑡 𝑑 −1 𝑖ℏ 𝑈 𝑡 𝑈 𝑡 = 𝐻 𝑑𝑡 (1) A Computer Algebra System takes it from here QUANTUM DYNAMICS WITH ALGEBRA Find a Lie algebra, with which a meaningful Hamiltonian is constructed. Find a decent ansatz for the time-evolution operator. 𝑎† , 𝑎, 𝑁, 𝐼 1 𝐻 = ℏ𝜔 𝑁 + + 𝑓 𝑡 𝑎 + 𝑎† 2 𝑈 𝑡 = 𝛼1 𝑡 𝑎† 𝛼2 𝑡 𝑎 𝛼3 𝑡 𝑁 𝛼4 𝑡 𝐼 𝑒 𝑒 𝑒 𝑒 (Wei-Norman Ansatz: A time-evolution operator group mapped to the Lie Algebra) WHAT EXACTLY ARE WE DOING MATHEMATICALLY? Computer produces 𝑑 −1 𝑖ℏ 𝑈 𝑡 𝑈 𝑡 = 𝐻 𝑑𝑡 We produce a model Hamiltonian 1 𝐻 = ℏ𝜔 𝑁 + + 𝑓 𝑡 𝑎 + 𝑎† 2 Ca a Ca a CN N CI H a a H a a H N N H I WE’RE DERIVING AN EXPLICIT FORM †OF THE TIME𝛼1 𝑡 𝑎 𝛼2 𝑡 𝑎 𝛼3 𝑡 𝑁 𝛼4 𝑈 𝑡 = 𝑒 𝑒 𝑒 𝑒 EVOLUTION OPERATOR 𝑡 𝑎 , 1 i1 if t 2 i 2 if t 3 i 4 if t 1 2i n U aU n n f U t ni Phase-space dynamics Transition probabilities 1 Hats are now left off from here on out unless necessary QUANTUM DYNAMICS WITH LIE ALGEBRA n U aU n n f U t ni Phase-space dynamics Transition probabilities 1 PART 2 – THE DIPOLE-FIELD MODEL 1 H t N f t a a 2 Initial single state n Final linear combination of time-dependent states: an n n 0 q f t f t t t EXTERNAL FIELD PULSE, THEN ATOMIC COLLISION f t Trajectories(Ehrenfest) field oscillator Laser Pulse Harmonic Oscillator Transition Probability 0 0 0 1 Atomic collision t t 0 Single initial state 𝑥 −10s = 0 t 0 t PERSISTENCE PROBABILITIES FOR THE OSCILLATOR (DIATOMIC MOLECULE) DURING THE EXTERNAL FIELD PULSE (COLLISION) 5 5 4 4 n 3 3 2 2 1 1 0 0 External dipole field sech 2 t t PART 2 – THE INELASTIC MOLECULAR COLLISION Three hard spheres, same mass, perfectly elastic collisions Three hard spheres, same mass, two of the three bound harmonically COLLINEAR COORDINATES One-dimension with 2 degrees of freedom RAB A B RBC No RAC interaction C LANDAU-TELLER MODEL HAMILTONIAN [AB + C] inelastic collision with reduced coordinates A B 𝑦 classical C 𝑥 − 𝑥0 quantum 1 2 1 2 1 2 y xˆ H pˆ x p y xˆ V0 e 2m 2 2 This is a semi-classical calculation because one variable is classical and the other is quantum. EXAMPLE OF INELASTIC COLLISIONS 𝑥 − 𝑥0 𝑦 INELASTIC COLLISION TRANSITION TIME Reduced mass relative collinear distance Trajectories Molecule Transition Probability molecule x t atom yt 0 0 0 1 0 2 0 0 0 1 0 2 Single initial state ti 0 t ti 0 Initial single ground state t INELASTIC COLLISION LANDSCAPE SINGLE Collision Bath Landscape Reduced mass relative collinear distance Trajectories atom yt molecu x t le Pi f t With a zero expectation value we can sum over final states from any initial state of choice. For any single state n , x is always zero. t RESONANCE: CLASSICAL WITH MORSE POTENTIAL Anharmonic interatomic potentials and different masses result in resonance t mA : mB : mC 2 : 12 : 1 Actual video! ALGEBRAIC CALCULATION APPLIED TO STATISTICAL MECHANICS PRINCIPLES Nuclear motion (Ehrenfest theorem) Collision Bath Landscape Pi f Single initial state •With a single initial state we can sum over final states from any initial state of choice •For any single state n , x is always zero for the harmonic oscillator t METHANE/HYDROGEN COLLISION Initial state 0 Transitions 0 2 1 0 Final state .94 .05 .01 PART 3 – THE REACTIVE MOLECULAR COLLISION REACTIVE COLLISIONS Collinear triatomic reaction: BG R B RG Reaction with a “Spectator”: SBG R SB RG REACTIVE COLLISIONS A Transition state or Activated complex RAB B RBC C POTENTIAL ENERGY SURFACE A B C A B C 1. Reactants 2. Transition state RAB 3. Products A B C 3. Total dissociation A RBC B C CURVILINEAR COORDINATES – BASED ON MINIMUM ENERGY PATHWAY OF POTENTIAL ENERGY SURFACE Products x s Transition state x quantum s classical 1 1 2 2 2 ps px V s, x H 2m where 1 x Reactants CURVILINEAR COORDINATE OR “IRC” Products x is perpendicular distance to the red line s0 x̂ The Frenet frame Transition state ŝ Reactants CURVILINEAR COORDINATES Products Transition state Reactants NATURAL COORDINATES SKEWING IS NECESSARY FOR SINGLE MASS ANALYSIS mb ma mb mc tan ma mc mass scaled and skewed coordinates CURVILINEAR COORDINATES Products x quantum s classical 1 1 2 2 2 ps px V s, x H 2m where 1 s x s x “curvature” Transition state Reactants THE DEVELOPMENT OF A REACTION COORDINATE Reaction Coordinate Harmonic Top view Anharmonic Top view VISUALIZING THE SINGLE-MASS INTERPRETATION LOOKING DOWN BOTH CHANNELS Reduced mass relative collinear distance A FULL MODEL WOULD ACCOUNT FOR POSSIBLE DISSOCIATION AS WELL- EXAMPLE: FESHBACH RESONANCE s t x s x Reduced mass relative collinear distance MATCH THE NUMBERS ON THE LEFT PLOT TO THE ASSOCIATED POSITION ON THE RIGHT s D t 1 B 3 x s 2 1 3 2 A B x A C Quantum Morse dissociation Pi f Could this the motion be related to the plot? 0 0 0 1 0 2 0 4 0 8 0 16 0 32 0 64 0 128 t REACTIVE COLLISION LANDSCAPE BATH Pi f t *Initial state of each collision is ground in a 1-indexed program* CONCLUSION How do I know my calculations are correct? Manuel and I compare our derivation of the EOM done by hand, twice over The derivation is then compared with Manuel’s Lie Algebra Coefficient Generator Program We compare our trajectories via Ehrenfest theorem to the classical limit model trajectories When needed we classically bin the bound phase-space motion to compare to quantum transitions We watch 𝑈 † 𝑈 𝑡 to make sure it does not leave unity What could we do that we CONCLUSION couldn't do before? Use the Hamiltonian as a generalized algebraic entity which has the potential to obviate numerical error in quantum dynamics Simultaneously analyze an oscillator’s motion with its quantum dynamics continuously throughout external interaction, with a more unified model than what we’ve seen in the literature Resolve the quantum dynamic details of a bath of collisions as they leave equilibrium Work from a foundation of optimized [Algebraic What predictions have you made CONCLUSION that need experimental verification? It’s not that I have specific predictions so much as the model is generalized to be able to compare to femtochemistry experiments, lasing, and nuclear reactions by specifying only a handful of parameters. We can predict state-to-state transition probabilities of an inelastic collision or a reaction from Reference Slides Begin Here CONCLUSION What experiments can we explain that we couldn't before? I’ve yet to find the femtochemist! The distribution of a fixed amount of energy among a number of identical particles depends of identical particles depends upon the density of available energy states and the probability energy states and the probability that a given state will be occupied. The probability that a given occupied. The probability that a given energy state will be occupied is given by the distribution occupied is given by the distribution function, but if there are more available energy states in a more available energy states in a given energy interval, then that will give a greater weight to the will give a greater weight to the probability for that energy interval. Quantum Morse dissociation Pi f 0 0 0 1 0 2 0 4 0 8 0 16 0 32 0 64 0 128 t HARMONIC VS. ANHARMONIC The Morse potential x2 12th order expansion of Morse potential 6th order expansion of Morse potential 4th order expansion of Morse potential CLASSICAL TRAJECTORY METHOD The de Broglie wavelength associated with motions of atoms and molecules is typically short compared to the distances over which these atoms and molecules move during a scattering process. Exceptions in the limits of low temperature and energy Separate A B into classical and quantum variables Mean free path >> “interaction region” C Reduced mass relative collinear distance INELASTIC COLLISION TRANSITION TIME SHOT 3 Amplitudes atom yt molecu x t le Molecule Transition Probability Initial single ground state 0 0 0 1 t tf t n t 2 Being found in n at t 0 2 t tf t n f U t ni 2 tf Conditional ti and on COMPARING DIFFERENT INITIAL STATES Triatomic mass ratio 1:3:1 Initial states Transitions 2 1 0 2 ni 1 0 Final states c1 c2 c3 TYPICAL DIATOMIC MOLECULE STP REFERENCES a v tv Relative velocity during collision h Ev h tv aEv v a h Diatomic molecule vibrational frequency Typical molecule has vibrational frequency of 1013 s -1 Estimate for intermolecular force range Gas phase molecular speeds are v about o a 2 1km s -1 v 2km s -1 vt 1 ROTATIONALLY ADIABATIC h E r tr vrt 100m s -1 2 or 3 orders of magnitude smaller than vib. spacing Gas phase molecular speeds are about tc rt tr v 1km s -1 rt 1 TRANSITION PROBABILITIES FOR THE DIATOMIC MOLECULE DURING THE COLLISION 5 5 4 4 n 3 3 2 2 1 1 0 0 External dipole field sech 2 t t INCREASING THE ATOMIC COLLISION SPEED 5 5 4 4 n 3 3 2 2 1 1 0 0 External dipole field sech 2 t t CANONICAL ENSEMBLE OF OSCILLATORS A “heat bath” f t B C Canonical Ensemble Microcanonical Ensemble •The canonical ensemble is initially at a defined temperature, though it can draw “infinite” amounts of energy from the heat bath, which are the collisions or external fields. •The microcanonical ensemble has a fixed energy TYPICAL RELAXATION TIMES FOR AN ENSEMBLE OF DIATOMIC MOLECULES ns N VT VR VV R T R R For external field induced or collision induced excitement of a diatomic molecule All other energy transfer types are quickly relaxed t E VS. T IN EXTERNAL FIELD t0 ns N VT Canonical ensemble of diatomic molecules initially at 400K Kcal/mol or Kelvin t f t Energy kcal/mol Temperature K t Diatomic molecule(6 d.o.f.) E vs. T in external field ENERGY VS. TEMPERATURE t1 ns N VT Nonequilibrium Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule E vs. T in external field TEMPERATURE UNDEFINED t3 ns N VT Nonequilibrium Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule E vs. T in external field ENERGY-TEMPERATURE t4 ns N VT Thermal equilibrium is reached again at 440K Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule E vs. T in external field E VS. T IN INELASTIC COLLISION t0 ns N VT Temperature = 400K Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule Atom E vs. T in inelastic collisions ENERGY VS. TEMPERATURE t1 ns N VT Nonequilibrium Temperature = ? Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule Atom E vs. T in inelastic collisions TEMPERATURE UNDEFINED t3 ns N VT Nonequilibrium Temperature = ? Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule Atom E vs. T in inelastic collisions ENERGY-TEMPERATURE t4 region of study ns N VT Thermal equilibrium is reached again Temperature = 440K Kcal/mol or Kelvin t Energy kcal/mol Temperature K t Diatomic molecule Atom E vs. T in inelastic collisions CANONICAL PHASE-SPACE DENSITY Thermal equilibrium is shown below as a Boltzmann distribution of oscillators quantum classical Density of states e n 1 kT 2 THERMAL NONEQUILIBRIUM Initially a Boltzmann distribution After collision, temperature undefined (extreme case) p y t p y t y t y t Part 1 - Time-dependent Hamiltonians When the Hamiltonian is timeindependent the time-evolution is simply When the Hamiltonian is time-dependent the time-evolution is rougher But what if the Hamiltonian does not commute with itself at different times? U t , t0 e U t , t0 e i H t t0 i t H t ' dt ' t0 H t1 , H t2 0 TRADITIONAL QUANTUM DYNAMICS •Differential equation approach d i x, t H t x, t dt H t H 0 H1 t leads to large O.D.E. system i E 0 E 0 t d 0 i 1 2 2 0 1 2 2 a f a f a f ... an an an ... e f n f0 * H1 n0 dt n selection rules emerge when looking for time-dependent transitions… a f1 t 2 TRADITIONAL QUANTUM DYNAMICS •Integral equation approach d i U t , t0 H t U t , t0 dt t i U t , t0 1 H t U t ' , t0 dt ' t0 Iterative form leads to 1. Dyson series 2. Volterra series 3. time-ordering 4. Magnus expansion NON-TRADITIONAL QUANTUM DYNAMICS •Algebraic approach A Lie algebra is a set of elements(operators) that is… 1. Closed under commutation 2. Linear 3. Satisfies Jacobi identity Example: Heisenberg-Weyl algebra: H2 I , x, p x, p iI Exponential mapping to the Lie-Group, the Heisenberg group GH e iaibxicp NON-TRADITIONAL QUANTUM DYNAMICS •algebraic approach Boson algebra Commutation relations U2 a, a , N , I a, a I a, N a Wei-Norman result for time-evolution operator U t e 1 t a 2 t a 3 t N 4 t I e e e (exponential map to the Wei-Norman time-evolution operator group) n f U t ni Transition probabilities 1 n U aU n Phase-space dynamics COMPUTERS EAT ALGEBRA IF FED CORRECTLY d i U t , t0 H t U t , t0 dt d 1 i U t U t H t dt Computer algebra system solves for any algebra U(N) Any Hamiltonian that is constructed of algebra U(N) EXAMPLE: HARMONIC OSCILLATOR IN A TIME-DEPENDENT EXTERNAL FIELD USING U(2) Computer produces Construct a Hamiltonian from the boson algebra d 1 i U t U t dt 1 H t N f t a a 2 Ca a Ca a CN N CI H a a H a a H N N H I THEN FIND THE EVOLUTION OPERATOR, U t e 1 t a 2 t a 3 t N 4 t e e e , 1 i1 if t 2 i 2 if t 3 i 4 if t 1 2i INELASTIC COLLISION LANDSCAPE BATH Amplitudes Reduced mass relative collinear distance atom yt Diatomic molecules leaving thermal equilibrium molecu x t le Pi f Single initial state t Density of states e n 1 kT 2 HARMONIC VS. ANHARMONIC The Morse potential x2 12th order expansion of Morse potential 6th order expansion of Morse potential 4th order expansion of Morse potential