* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download document 8171030
Hidden variable theory wikipedia , lookup
Density matrix wikipedia , lookup
Matter wave wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Wave–particle duality wikipedia , lookup
Coupled cluster wikipedia , lookup
Renormalization group wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Second quantization wikipedia , lookup
Perturbation theory (quantum mechanics) wikipedia , lookup
Path integral formulation wikipedia , lookup
Scalar field theory wikipedia , lookup
Self-adjoint operator wikipedia , lookup
Compact operator on Hilbert space wikipedia , lookup
Coherent states wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Canonical quantum gravity wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Dirac bracket wikipedia , lookup
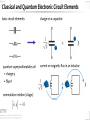
k g vz xz f Quantization of the electrical LC harmonic oscillator: parallel LC oscillator circuit: voltage across the oscillator: total energy (Hamiltonian): with the charge Q stored on the capacitor a flux f stored in the inductor properties of Hamiltonian written in variables Q and f Q and f are canonical variables see e.g.: Goldstein, Classical Mechanics, Chapter 8, Hamilton Equations of Motion Quantum version of Hamiltonian with commutation relation compare with particle in a harmonic potential: analogy with electrical oscillator: - charge Q corresponds to momentum p - flux f corresponds to position x Hamiltonian in terms of raising and lowering operators: with oscillator resonance frequency: Raising and lowering operators: number operator in terms of Q and f with Z c being the characteristic impedance of the oscillator charge Q and flux f operators can be expressed in terms of raising and lowering operators: Exercise: Making use of the commutation relations for the charge and flux operators, show that the harmonic oscillator Hamiltonian in terms of the raising and lowering operators is identical to the one in terms of charge and flux operators.