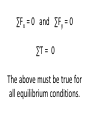Download Equilibrium is not just translational, is is also rotational. While a set

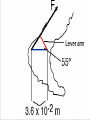
Equilibrium is not just
translational, is is also
rotational. While a set of
forces may not change
the velocity of an object,
it may change its speed
of rotation.
The lever arm is the
distance between the
line of action (direction
of force applied) and
the axis of rotation.
Torque Ƭ is the
magnitude of the
force multiplied by
the lever arm.
Ƭ = Fl
The torque is positive if the
force tends to produce a
counterclockwise rotation, and
negative if it tends to produce a
clockwise rotation.
The unit is the newton•meter
(N•m).
Ex. 1 - A force whose
magnitude is 55 N is applied
to a door. However, the lever
arms are different lengths in
each of three cases:
(a) l = 0.80 m, (b) l = 0.60 m,
(c) l = 0. Find the magnitude
of the torque in each case.
Ex. 2 - In your ankle joint, your
Achilles tendon is attached to the
heel. If the tendon exerts a force of
F = 720 N at a n angle of 55° to the
lever arm, find the torque of this
force about the ankle joint, which
is 3.6 x 10-2 m from the point of
attachment.
If a rigid body is in equilibrium its
motion does not change. Therefore,
the net force is zero. For twodimensional motion, the sum of the x
and y components of the forces are
both zero. In these conditions, we
exclude all internal forces, because
these are all action-reaction pairs.
Under equilibrium conditions,
there is also no net torque.
If there is a net torque, the
object will undergo angular
acceleration.
If an object is in equilibrium,
there is no translational
acceleration and no rotational
acceleration.
∑Fx = 0 and ∑Fy = 0
∑Ƭ = 0
The above must be true for
all equilibrium conditions.
Ex. 3 - A woman whose weight is
530 N is poised at the right end of a
diving board, whose length is 3.90 m.
The board has negligible weight and is
bolted down at the left end, while
being supported 1.40 m away by a
fulcrum. Find the forces F1 and F2 that
the bolt and the fulcrum, respectively,
exert on the board.
The location of the axis is
completely arbitrary,
because if an object is in
equilibrium, it is in
equilibrium with respect
to any axis whatsoever.
Ex. 4 - An 8.00-m ladder of weight
WL = 355 N leans against a smooth vertical
wall. The wall exerts only a normal force and no
frictional force. A firefighter, whose weight is
WF = 875 N, stands 6.30 m from the bottom of
the ladder. Assume that the weight of the ladder
acts at the ladder’s center and neglect the
weight of the hose?!?! (Leggs, maybe?) Find the
forces that the wall and ground exert on the
ladder.
Choosing the direction
of an unknown force
backward in the free-body
diagram simply means that
the value determined for
the force will be a negative
number.
Ex. 4 - A body builder, strengthening
his shoulder muscles, holds a dumbbell
of weight Wd. his arm is extended horizontally
and weighs Wa = 31.0 N. The deltoid muscle is
assumed to be the only muscle acting. The
maximum force M that the deltoid muscle can
supply is 1840 N. What is the weight of the
heaviest dumbbell that can be held, and what
are the horizontal and vertical force
components, Sx and Sy , that the shoulder joint
applies to the left end of the arm?