* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Mechanical Systems - Rose
Brownian motion wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Hamiltonian mechanics wikipedia , lookup
Coriolis force wikipedia , lookup
Modified Newtonian dynamics wikipedia , lookup
Center of mass wikipedia , lookup
Analytical mechanics wikipedia , lookup
Specific impulse wikipedia , lookup
Relativistic quantum mechanics wikipedia , lookup
Lagrangian mechanics wikipedia , lookup
Newton's theorem of revolving orbits wikipedia , lookup
N-body problem wikipedia , lookup
Classical mechanics wikipedia , lookup
Hunting oscillation wikipedia , lookup
Angular momentum operator wikipedia , lookup
Fictitious force wikipedia , lookup
Accretion disk wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Velocity-addition formula wikipedia , lookup
Jerk (physics) wikipedia , lookup
Photon polarization wikipedia , lookup
Derivations of the Lorentz transformations wikipedia , lookup
Matter wave wikipedia , lookup
Relativistic mechanics wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Routhian mechanics wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Centripetal force wikipedia , lookup
Equations of motion wikipedia , lookup
Classical central-force problem wikipedia , lookup
Kinematics
Mechanical Systems
mv G 1
mv G 2
ImpulseMomentum
I G ω2
r
Psys 2
r
L sys O
(
=
−
)
−
2
I G ω1
r
Psys1
r
L sys O
(
=
)
=
1
∫ F dt
1
∫ F dt
2
∫ Mdt
r
∑ Fr∆ t ,
∑ (M ) ∆ t
i
O i
F
Newton’s
Second Law
Conservation of Energy
∆E sys = W
Work:
2
2
r r
W = F ⋅ d s , W = Mdθ
∫
1
F
m(αr)
IGα
E sys = E k + E G + E s + U
W
2
dPsys
dt
r
dL sys o
dt
Ox
Free Body
Diagram
=
=
1
Energy:
Oy
m(ω
r)
Kinetic
Diagram
r
∫
∑
r
F
∑
r
Mo
where
EG = mgz (Gravitational potential energy)
Es =
1 2
kx
2
(Elastic potential energy linear
spring)
1
1
mv G2 + I G ω2 (Kinetic energy (plane motion)
2
2
U (Internal energy)
Ek =
Table of Contents
Chapter 1 – Introduction .......................................................................................1–4
1.1 A Bit of History..........................................................................................1–2
1.2 An overview of the class ...........................................................................1–10
1.3 The general problem solving methodology ...............................................1–15
Chapter 2 Review of Conservation Principles and Basic Kinematics ...................2–1
2.1 Basic Kinematics.........................................................................................2–2
2.2 Conservation of Linear Momentum (general comments)............................2–7
What is linear momentum?........................................................................2–7
How do you calculate the linear momentum of a system of particles? .....2–8
How can linear momentum be transported? ..............................................2–9
How can linear momentum be generated or destroyed?..........................2–11
2.3 Conservation of Linear Momentum (Rate Form).....................................2–12
2.3.1
Procedure for applying the rate form of conservation of linear
momentum (Newton’s 2nd law) to particles.................................................2–14
2.3.2 Frictional forces..................................................................................2–25
2.4 Conservation of Linear Momentum (Finite Time) ...................................2–29
2.4.1 Procedure for applying the conservation of linear momentum (finite time
form) to particles .........................................................................................2–29
2.4 Conservation of Angular Momentum........................................................2–35
What is angular momentum?...................................................................2–35
How do you calculate the angular momentum of a system of particles?.2–38
How can angular momentum be transported into or out of a system?.....2–38
How can angular momentum be generated or destroyed?.......................2–39
Common situations..................................................................................2–40
Modeling Reactions at Supports and Connections ..................................2–40
2.5 Conservation of Energy.............................................................................2–47
Mechanical Work ....................................................................................2–49
Mechanical Power ...................................................................................2–51
Conservation of Energy from Conservation of Linear Momentum.........2–51
Elastic Potential Energy ..........................................................................2–53
2.6 Summary of the Conservation Principles to be Used ................................2–64
2.6.1
Procedure for applying the rate form of conservation of linear
momentum (Newton’s 2nd law) to particles.................................................2–68
2.6.2 Procedure for applying the finite time form of conservation of energy to
particles .......................................................................................................2–68
2.6.3 Procedure for applying the conservation of linear momentum (finite time
form) to particles .........................................................................................2–69
Problems......................................................................................................... .2-71
Chapter 3 Particle Kinematics and Dynamics .......................................................3–1
3.1 Relative Motion...........................................................................................3–2
3.2 Dependent Motion.......................................................................................3–7
3.3 Different Coordinate Systems ...................................................................3–15
3.3.1 Cartesian Coordinates.........................................................................3–15
3.3.2 Normal and Tangential Coordinates...................................................3–16
3.3.3 Radial and Transverse Coordinates ....................................................3–26
3.3.4 Summary of Different Coordinate Systems........................................3–34
3.4 Impact........................................................................................................3–35
3.4.1 Comments on the coefficient of restitution ........................................3–39
Problems..........................................................................................................3-51
Chapter 4 – Rigid Body Dynamics........................................................................4–1
4.1 Introduction .................................................................................................4–2
4.2 Translation...................................................................................................4–3
4.3 Rigid Body Rotation ................................................................................... 4–6
4.3.1 Basic Kinematic Relationships ............................................................ 4–6
4.3.2 Fixed Axis Rotation ........................................................................... 4–9
4.3.3 Comments on applying the conservation principles .......................... 4–12
4.3.4 Rigid Body Impact............................................................................. 4–21
4.4 General Plane Motion ............................................................................... 4–24
4.4.1 Velocity............................................................................................. 4–24
4.4.2 Instantaneous Center of Velocity...................................................... 4–28
4.4.3 Accelerations ..................................................................................... 4–41
4.5 Rotating Axis ............................................................................................ 4–56
Problems ..........................................................................................................4-69
Appendix A - Mass Moments of Inertia ............................................................... A1
A.1 What is the mass moment of inertia? ..........................................................A2
Chapter 1 – Introduction
In this chapter I will present a brief history of dynamics and try to give you an
overview of what we will be discussing in this book.
Sir Isaac Newton from a portrait
by Enoch Seeman in 1726
Portrait of Leonhard Euler
1–2
1.1 A Bit of History
In this section I will present a brief history of dynamics from Newton to Hamilton.
If you are not interested in the history of dynamics just skip to the next section.
The reference I used to obtain much of this historical information is Fundamentals
of Applied Dynamics by James Williams. The biographical information came
primarily from a couple of wonderful websites, http://www-groups.dcs.stand.ac.uk/~history/Indexes/Full_Alph.html and Eric Weissteins’ World of
Scientific Biography (http://scienceworld.wolfram.com/biography/), both of which
had huge collections of short biographies.
Ancient
Aristotle
Dynamics has evolved along two primary lines of thought, the direct approach and
the indirect approach. Some of the main contributors to each approach are shown
in Figure 1.1.
Galileo Galilei
Direct
Approach
- Newton
- Euler
Indirect
Approach
The direct approach, also called vectorial dynamics, has the following
characteristics:
• Force and momentum are primary parameters
• Newton’s laws are considered directly so we get vector equations
The indirect approach, or variational dynamics (also called analytical dynamics), is
an alternative method of obtaining governing differential equations and is
characterized by the following:
• Forces that do no work do not need to be considered
• Accelerations do not have to be computed, only velocities
• In general, operations are on scalars not vectors
A time line showing when some of the primary contributors to dynamics lived is
shown in Figure 1.2. The number in the bar is how old he was when he died and the
number on the left is the year of his birth. The purpose of this figure is to give you
a sense of when they lived relative to each other and how most of the material
covered in this text is really quite old, although our approach to it will be a bit
different.
- Leibniz
- John Bernoulli
- D’Alembert
- Euler
- Lagrange
- Hamilton
Figure 1.1 Two lines of thought when
solving dynamics problems
1805
Hamilton
1736
Lagrange
1717
D'Alembert
1707
Euler
1667
Bernoulli
1646
70
Newton
1642
85
1564
1400
1450
1500
1550
77
66
76
81
Leibniz
Galileo
60
78
1600
1650
1700
1750
1800
1850
Figure 1.2 Some of the primary contributors to dynamics and when they lived.
1900
1–3
It is important to recognize that there are additional individuals who are clearly
important to the development of dynamics, but I will try to focus on those I believe
to be the major contributors. Brief summaries of the lives of these men, and a few
earlier ones, and some of their contributions to the field of dynamics are listed
below.
Aristotle (384-322 B.C.)
Aristotle is generally classified as one of the greatest philosophers of all time. The
main reason for briefly mentioning him in this short discussion of the history of
dynamics is that his works were accepted as fact for a very long time. Quoting D J
Allan from The Philosophy of Aristotle (1978):
Aristotle
Aristotle, more than any other thinker, determined the orientation and the
content of Western intellectual history. He was the author of a philosophical
and scientific system that through the centuries became the support and vehicle
for both medieval Christian and Islamic scholastic thought: until the end of the
17th century, Western culture was Aristotelian. And, even after the intellectual
revolutions of centuries to follow, Aristotelian concepts and ideas remained
embedded in Western thinking.
He did work in fields that we now classify as biology, astronomy, physics,
chemistry, logic, metaphysics, theology, psychology, politics, economics, and
others. Aristotle was the first to conceive of and establish many of these fields of
study as systematic disciplines. From “Treatise on the Heavens and Physics,” his
views regarding terrestrial motion can be summarized as follows:
• The natural state of all earth bound bodies is rest (zero velocity)
• Objects fall in a straight line
• Heavy objects fall faster than light objects
• If a given object falls from a certain height in a particular time interval, an
object that is twice as heavy will fall from the same height in half the time
interval.
Based simply on observation, all of these propositions sound perfectly reasonable
and are consistent with everyday experience, however, they are wrong. This was
basically the state of understanding for approximately 2000 years.
Galileo Galilei (1564-1642)
Galileo was a true Renaissance man. Not only was he a philosopher and scientist,
but also an excellent lute player (his father was a professional musician) and
painter. He attended medical school in Padua and in 1592 he was appointed
professor of mathematics at the university there. He primarily taught geometry and
standard (geocentric) astronomy to medical students. You must remember that
times were quite different then and so was the medical profession. His students
were required to know some astronomy in order to make use of astrology in their
medical practice.
Portrait of Galileo by Justus
Sustermans painted in 1636
Galileo built his own telescope in 1609 and he discovered craters and mountains on
the moon, sun spots, the four largest moons of Jupiter and that the planet Venus
1–4
showed phases like those of the moon, indicating that it must orbit the sun rather
than the Earth.
I’ll only mention a few of his ideas which strongly influenced dynamics. By 1604
he had determined the correct relationship for falling bodies (d ∝ t2) and had stated
that bodies of different weights should fall at the same speed (the difference being
because of air resistance). In “Dialogue Concerning the Two Chief World Systems”
(1632), he conducted a thought experiment in which he concluded that the natural
state of motion for a body is constant velocity. This was a key to the concept of
inertia and the development of dynamics.
“Dialogue Concerning the Two Chief World Systems” was supposed to be an
objective debate between the Copernican and Ptolemaic systems. Unfortunately,
Galileo put the Pope's favorite argument in the mouth of one of the characters, then
proceeded to ridicule it (which, by the way, is not a good idea unless you happen to
be a good friend of the Pope and you know he has a good sense of humor, which
Galileo wasn’t and the Pope didn’t). Galileo suddenly lost favor with the church,
was forced to recant his Copernican views and was condemned to house arrest, for
life, at his villa at Arcetri (above Florence). He was also forbidden to publish.
Isaac Newton (1642-1727)
The most famous person associated with the study of dynamics is Sir Isaac Newton,
affectionately called “needle nose Newton” by his closest friends. That last part is
not true, so please don’t quote me. Newton made truly amazing contributions to
science and mathematics. As famous poet Alexander Pope wrote:
"Nature and Nature's laws lay hid in night; God said, Let Newton be! and all
was light."
Sir Isaac Newton from a
portrait by Kneller in 1702.
This is in the National
Portrait Gallery in London.
Newton was still under 25 years old when he began making revolutionary advances
in mathematics, optics, physics, and astronomy. Newton invented calculus years
before Leibniz, although he did not publish his work. This led to a significant
conflict between those supporting Newton and those supporting Leibniz, basically,
English and continental mathematicians, respectively. Although Newton is now
generally acknowledged as having done the work earlier than Leibniz, Leibniz had
a superior notation, a notation that is still used today. Newton seemed to be
characterized by a lack of publishing for much of his life. This may have been due
to the fact that he was very sensitive to criticism (possibly from being picked on as
a child ... OK, I made that up). For example, the conflict he had with Robert
Hooke over optics resulted in his ceasing all publications until after the death of
Hooke in 1703.
Newton’s most significant work on physics, generally acknowledged as one of the
most important and influential works in science of all time, was called
Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural
Philosophy) (1687), or more commonly referred to as The Principia (1687). This
work contains three books. In Book I he states the three laws that he presumes
governs the motion of all objects (see Table 1.1) as well as the law of universal
gravitation.
1–5
Table 1.1 - Newton’s Three Laws
Law
1
2
3
Original statement
Every body continues in its state of rest or of
uniform motion in a right line, unless it be
compelled to change that state by forces
impressed upon it.
The change of motion is proportional to the
motive force impressed; and is made in the
direction of the right line in which that force
is impressed.
To every action there is always opposed an
equal reaction; or, the mutual actions of two
bodies upon each other are always equal, and
directed to contrary parts.
Modern statement
A particle remains at rest or continues to move in a
straight line with constant velocity if there is no
resultant force acting on it.
A particle acted on by a resultant force moves in
such a manner that the time rate of change of its
linear momentum is equal to the force.
Forces result from the interaction of particles and
such forces between two particles are equal in
magnitude, opposite in direction, and collinear.
Later in life, Newton worked as a highly paid government official in London with
little further interest in mathematical research. I thought you might be interested in
knowing a few other facts about Newton. Newton believed deeply in the necessity
of a God. His theological views are characterized by his belief that the beauty and
regularity of the natural world could only "proceed from the counsel and dominion
of an intelligent and powerful Being." He felt that "the Supreme God exists
necessarily, and by the same necessity he exists always and everywhere." I agree
with this view. Even though he had, in my opinion, a reasonable and logical view
of God, doesn’t mean he didn’t go down some wrong paths. For example, he
devoted a majority of his free time later in life (after 1678) to fruitless alchemical
experiments which likely explains the large amount of mercury that was found in
his body following his death. Finally, a few quotes attributed to him.
“If I have been able to see further, it was only because I stood on the shoulders
of giants,” from a letter to Robert Hooke.
“I know not what I appear to the world, but to myself I seem to have been only
like a boy playing on the sea-shore, and diverting myself in now and then
finding a smoother pebble or a prettier shell, whilest the great ocean of truth
lay all undiscovered before me.” Quoted in Memoirs of Newton by D.
Brewster,
Gottfried Leibniz (1646-1716)
Leibniz was a German philosopher, mathematician and physicist (you’ll note that at
this time there was not much of a distinction between these fields). Leibniz made
major contributions to the field of mathematics and is credited with developing
calculus independent of Newton (and with much superior notation that is still in use
today). He also did work in the area of differential equations as well as many other
areas, but let’s talk about his more interesting work in the area of dynamics. OK,
more interesting from my perspective. If you want to read more about what he did
in math then take a math class, this is dynamics.
Portrait of Gottfried
Leibniz
1–6
Leibniz was a strong believer in what he called vis visa, the living force, which was
equal to mv2. He believed his vis visa to be the most fundamental quantity (in
contrast to Descartes’ momentum, mv) for describing motion. He believed the
amount of vis visa did not change and his statements come very close to an early
statement of conservation of energy. This was the beginning of what we now call
“energy methods” in dynamics. What is interesting to me is that he argued for this
conserved quantity, not so much on the basis of experimentation since inelastic
collisions seem to contradict his assertion that this quantity did not change, but
more from a belief in the order and continuity of the world. He believed the world
had order because it had been created by God.
Finally, I want to share how some others have described him. In the biography of
Leibniz in Encyclopaedia Britannica he is described as follows:
“Leibniz was a man of medium height with a stoop, broad-shouldered but
bandy-legged, as capable of thinking for several days sitting in the same chair
as of traveling the roads of Europe summer and winter. He was an
indefatigable worker, a universal letter writer (he had more than 600
correspondents), a patriot and cosmopolitan, a great scientist, and one of the
most powerful spirits of Western civilization.”
Another quote about him attributed variously to Charles Louis de Secondat
Montesquieu and to the Duchess of Orléans:
“It is rare to find learned men who are clean, do not stink and have a sense of
humor.”
John Bernoulli (1667-1748)
The Bernoulli family was truly amazing in the number of family members who
made significant contributions to mathematics and science. They were also a
family beset with jealousy, rivalry and bitterness. In other words, their family
reunions were probably not very fun, and not only because they were a bunch of
mathematicians (I can say this because my father was a mathematician). There are
a number of things that have been named “Bernoulli’s _____” such as “Bernoulli’s
equation”, “Bernoulli numbers”, “Bernoulli’s principle” and so on. Unfortunately,
they usually don’t refer to the same Bernoulli. A Bernoulli family tree is shown in
Figure 1.3 (only the family members who were well known mathematicians are
shown.) Although I am going to talk about Johann (John) Bernoulli the most, I
thought you might be interested in some of the others and some of the things named
after them.
Portrait of John Bernoulli
Nicolaus
1623-1708
Jacob
1654-1705
Nicolaus
1662-1716
Johann
1667-1748
Nicolaus (I)
1687-1759
Nicolaus (II)
1695-1726
Johann (III)
1744-1807
Daniel
1700-1782
Daniel (II)
1751-1834
Johann (II)
1710-1790
Jacob (II)
1759-1789
Figure 1.3 - Members of the Bernoulli
family who were excellent mathematicians
and/or physicists.
In mathematics, Bernoulli’s equation y ′ = p( x ) y + q ( x ) y n
is named after Jacob
Bernoulli, as are the Bernoulli numbers. Daniel Bernoulli showed that as the
velocity of a fluid increases, the pressure decreases, a statement known as the
Bernoulli Principle and the equation describing the flow of an incompressible,
inviscid, steady fluid is called Bernoulli’s equation. He also won the annual prize
of the French Academy ten times for work on vibrating string, ocean tides, and the
kinetic theory of gases. Only Leonhard Euler won this prize more times.
1–7
Now let’s talk about John (Johann) Bernoulli. First some trivia: I’m sure you have
all learned l'Hospital's rule in one of your math classes. It turns out that Johann
instructed l'Hospital in calculus. l’Hospital later wrote a textbook based on
Bernoulli’s instruction to him and in this book he included what is now known as
l’Hospital’s rule. This rule had actually been developed by Bernoulli. It is
probably better that it was not proved to be John’s result before 1922 because there
would have been something else named after a Bernoulli, Bernoulli’s rule. In a
letter in 1717 he precisely formulated the “Principle of Virtual Work” (for all
admissible variations, the sum of all the work done by the forces must vanish if the
forces are in equilibrium) which is a crucial concept in variational dynamics. His
most famous student was Leonhard Euler.
Portrait of Leonhard Euler
Leonhard Euler (1707-1783)
All of the men I am discussing were extremely brilliant and hardworking, but Euler
stands out in my mind as particularly amazing. I don’t know if it is true, but I read
that he once did a calculation in his head to settle an argument between two
students whose computations differed in the fiftieth decimal place. He also appears
to have had a photographic memory. It is said that early in his life he memorized
the entire Aeneid by Virgil and at age 70 he could not only recite the entire work,
but could also state the first and last sentence on each page of the book he had
memorized it from. His memory and his ability to do calculations and analysis in
his head served him well considering the fact that he was totally blind the last 17
years of his life. Blindness did not seem to hinder him in any way since he
produced almost half of his total works while he was completely blindness. Euler
was the most prolific writer of mathematics of all time, averaging 800 printed
pages/year throughout his life. When asked for an explanation why his memoirs
flowed so easily in such huge quantities, Euler is reported to have replied that “his
pencil seemed to surpass him in intelligence”. His choice of Leibniz’s differential
notation led the way towards our modern notation and techniques in mechanics. He
made major contributions in dynamics, solid mechanics, fluid mechanics, optics,
electricity, magnetism, and mathematics to name a few fields. Over 30 quantities
(equations, numbers, theorems, etc) are named after him. For example: Euler's
formula (eiθ=cosθ+isinθ), Euler's equation (in the calculus of variations), Euler's
equation (in differential equations), Euler's equation (for the motion of an ideal
fluid), and Euler's equations (for the rotation of a rigid body) just to name a few. In
other words, just saying “Euler’s equation” doesn’t give nearly enough information
because there are too many equations named after him.
Let’s talk about his work in the area of mechanics. Euler was the person to extend
Newton’s concepts to rigid bodies (Newton was basically concerned with
particles), so if you don’t like rigid body dynamics (although I can’t imagine this to
be the case since it is much more interesting and fun than particle dynamics), you
have Euler to blame and not Newton. Euler had several major works in mechanics
including Mechanica (1736), which provided a major advance in mechanics
primarily due to the systematic and successful way he presented Newtonian
dynamics in the form of mathematical analysis for the first time. In 1765 he
published Theoria motus corporum solidorum (Theory of the Motions of Rigid
Bodies) in which he decomposed the motion of a solid into a rectilinear motion and
a rotational motion and laid the foundation of analytical mechanics. Euler’s work
1–8
provided the key to solving such problems as the movement of gyroscopes,
spinning tops, the nutation of the earth, and a host of related problems. A major
step toward the solution of such problems was the definition of concepts such as the
“center of inertia” and the “moment of inertia,” which Euler first calculated for
various homogenous bodies.
Finally, I’d like to share a few quotes and a final comment on this amazing man. In
a testament to Euler's proficiency in all branches of mathematics, the great French
mathematician Laplace (you know him for the Laplace transform) told his students,
"Liesez Euler, Liesez Euler, c'est notre maître à tous" ("Read Euler, read Euler, he
is our master in everything" (Beckmann, P. A, History of Pi, 3rd ed. New York:
Dorset Press, 1989). Euler also had 13 children (although only five of them lived to
adulthood) and he claimed that some of his greatest discoveries were made while
holding a baby in his arms with his other children playing around his feet. Based
on everything I read, in addition to being brilliant and extremely hard working,
Euler was a gracious and unselfish person, a loving father, a teacher, and a man of
deep faith and conviction.
Portrait of Jean Le
Rond d-Alembert
Jean Le Rond d’Alembert (1717-1783)
D’Alembert was a French mathematician. With Diderot he worked on the 28
volume encyclopedia Dictionaire raisonné des sciences, des arts et des métiers (the
first volume appeared in 1751). D'Alembert wrote most of the mathematical and
scientific articles and the work was widely acclaimed. His main contribution to
dynamics was in Traité de Dynamique (1743) where he presents what is now
known as d’Alembert’s principle which reduces problems of dynamics to statics by
adding a new force called the “inertial force” (F-ma=0). Many people who teach
dynamics don’t like d’Alembert’s principle since mass times acceleration is not
really a force and we hate to see students getting confused. We will never use
d’Alembert’s principle in this book and you will never, ever find a mass times
acceleration term on a free body diagram! The main reason for including him in
this brief history is that his work strongly influenced the pursuit and development
of minimum principles by Lagrange and Hamilton.
One final piece of trivia concerning d’Alembert: As a baby, he was abandoned by
his mother on the steps of the church of St. Jean Baptiste de Rond where he was
found and taken to a home for homeless children. He was named after the church.
Joseph-Louis Lagrange (1736-1813) Lagrange is the first of the men I have
discussed so far who viewed himself almost exclusively as a pure mathematician
who sought mathematical elegance. In his most famous work on mechanics,
Mechanique Analytique (1788), he states in the preface:
“No diagram will be found in this work. The methods that I explain in it
require neither construction nor geometrical or mechanical arguments, but only
the algebraic operations inherent to a regular and uniform process. Those who
love Analysis will, with joy, see mechanics become a new branch of it and will
be grateful to me for thus having extended its field.”
Portrait of Joseph-Louis
Lagrange
This view is in complete contrast to what I will try to encourage you to do as you
attack problems in this class, that is, I want you to DRAW PICTURES! In
1–9
particular I will encourage you to draw a “Free Body Diagram” and “Kinetic
Diagram.” In Mécanique Analytique, Lagrange summarized all the work done in
the field of mechanics since the time of Newton and it is notable for its use of the
theory of differential equations. In this work Lagrange also laid the foundation for
variational dynamics, generalized the Principle of Least Action (which states that
nature chooses the most economical path for moving bodies and was first
formulated by Pierre de Maupertuis), and presented a new and very powerful tool
for deriving equations of motion, now called “Lagrange’s equations”. We will not
use Lagrange’s equations in this book, but if you continue your study of dynamics
you will certainly come across it.
Portrait of GustaveGaspard Coriolis
Gustave-Gaspard Coriolis (1772-1843)
Like all of the men discussed in this section, Coriolis was a very bright guy. After
all, you don’t ask a slacker to succeed Navier (of the famous Navier-Stokes
equation in fluids) as the chair of applied mechanics at the École des Ponts and
Chaussées and to become a member of the Académie des Sciences as Coriolis was
in 1836, but to be perfectly honest, I wouldn’t place him in the same category as
those I have discussed so far. Why am I discussing him then? His name will
appear when we discuss rotating coordinate systems so I thought you might be
interested in who he was. His primary areas of research were engineering
mathematics and mechanics, in particular friction and machine performance. He
introduced the terms “kinetic energy” and “work” with their modern scientific
meanings, but he is most known for the Coriolis acceleration term that appears
when using rotating coordinate frames. He first discussed this in the paper "Sur les
équations du mouvement relatif des systèmes de corps" (1835). Now for some
trivia: Coriolis proposed a unit of work, called the 'dynamode.' Personally, I like it
better than joule or foot-pound or BTU or whatever other modern unit we may
place on work. Dynamode sounds cooler.
Sir William Hamilton (1805-1865)
I want to briefly mention one other individual, William Hamilton. Hamilton
extended the formulation of Lagrange by giving the first exact formulation of the
Principle of Least Action. This is now called Hamilton’s Principle, and similar to
Lagrange’s Equations, if you continue to study the field of dynamics you will
undoubtedly come across and use Hamilton’s Principle at some time. A few pieces
of trivia concerning Hamilton: As a child, his linguist uncle James taught him 14
languages, and unfortunately, Hamilton was an alcoholic for the last third of his
life.
Sir William Hamilton
Clearly the short snippets I’ve included about these giants in the field of dynamics
leave out a lot of details and interesting facts. Also, there are others who made
significant contributions to the field of dynamics before, during and after the time
these men lived. Since I could not discuss them all, I wanted to give you a brief
snapshot of the ones who, in my opinion, made the most significant contributions
prior to the 20th century, because you no doubt have heard their names in the past
or will hear their names in the future.
1–10
1.2 An overview of the class
&
B
in
&
B
out
dB sys
dt
System
dBsys
dt
& −B
&
=B
in
out
Figure 1.4 - System accounting
for a conserved quantity B
Before we discuss the principles we will be using in this class I want you to have a
feel for how these principles fit into the larger context of engineering science. In
this class, as in most of your engineering science classes, the concept of a “system”
is crucial. A system is anything we set aside for analysis, and it is very important
that you clearly identify your system when solving a problem. After deciding on a
system, we need to decide what principle or principles to use. A generic illustration
of a conservation principle is shown in Figure 1.4. If we have some extensive
property, B, we know that if B is conserved then the rate of B entering the system
minus the rate of B leaving is equal to the rate of change of B inside the system. In
this book, when we state that a property is conserved we simply mean that it cannot
be created or destroyed. The basic conservation and accounting principles (written
in their rate forms) are:
Conservation of Mass:
dm sys
dt
=
∑ m& −∑ m&
i
in
o
out
Conservation of Charge:
dq sys
dt
=
∑i −∑i
i
in
Conservation of Linear Momentum:
r
r
dPsys
=
F+
dt
o
out
∑ ∑ m& v −∑ m&
i
r
i
in
r
o vo
out
Conservation of Angular Momentum:
r
r
dL sys0
r
r
r
r
& o vo
& i vi −
=
Mo +
r ×m
r×m
dt
in
out
∑
Conservation of Energy:
dE sys
& +W
& +
=Q
dt
Accounting of Entropy:
dS sys
dt
∑
in
=
∑
∑
v2
& i h +
+ gz −
m
2
i
∑
out
v2
& o h +
+ gz
m
2
o
&
Q
∑ T + ∑ m& s − ∑ m& s + S&
i
in
o
GEN
out
The first five of these statements are conservation principles and the last one,
entropy, is an accounting principle since entropy can be generated. In the study of
dynamics, we will primarily use only three of these principles: conservation of
linear momentum, conservation of angular momentum and conservation of energy.
The reason I am showing you all of the equations shown above is so that you can
see the similar form of all the conservation principles. Also, you should keep in
mind that the ways we will use the principles in this book contain a number of
assumptions. For example, when we use conservation of energy we typically
assume a closed adiabatic system. Also, when you encounter these principles in
other courses, and they look different because different assumptions are being made
in that course, you will recognize that it is really the same principle.
1–11
Let’s talk about dynamics. The study of dynamics can be broken down into two
primary areas, kinetics and kinematics, as shown below.
Dynamics
The branch of mechanics that deals
with the motion of bodies under the
action of forces.
Kinematics
Kinetics
“The geometry of the motion.”
Describing the motion of bodies without
reference to the forces that either cause
the motion or are generated as a result of
The relations between
unbalanced forces and the
changes in motion they
d
The kinetics portion of dynamics is basically the conservation principles, that is, I
have a system acted upon by the surroundings and I want to determine the
subsequent motion or forces. In this book we will be using conservation of linear
and angular momentum (rate form), conservation of energy (finite time form) and
conservation of linear and angular momentum (finite time form). Unfortunately,
not everyone calls these principles by the same name. For example, what I will call
“the rate form of conservation of linear momentum” will be called “direct
application of Newton’s 2nd Law” by many people. You need to have the maturity
and flexibility to understand that they are referring to the same thing, and in this
book I will use the names interchangeably. You should have seen these kinetics
principles in earlier courses, but I will review them in the next chapter. The
conservation principles we will use to solve kinetics problems (plus their
alternative names) are shown below.
Dynamics
Kinetics
Rate Form of Linear and
Angular Momentum
(Direct Application of
Newton’s 2nd Law)
Kinematics
Finite Time Form
of Conservation of
Energy (WorkEnergy Methods)
Finite Time Form of
Linear and Angular
Momentum (ImpulseMomentum Methods)
The main thing we need to add to these conservation principles in order to solve a
large variety of problems is kinematics. I like to call kinematics “the geometry of
the motion”, that is, I don’t care what is causing the motion, I want to describe it.
How does one describe motion? With terms like “position”, “velocity”,
1–12
“acceleration”, etc. Again, you should have already seen some basic kinematic
relationships, but they will be reviewed in the next chapter. A concept map of all
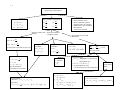
of the kinematics we will discuss in the class is shown in Figure 1.5.
Kinematics
(the geometry of the motion)
Relative
motion
Basic kinematic
relationships for
position, velocity and
acceleration
Separate variables and
integrate
Represent in different
coordinate systems
Acceleration
not constant
Constant
acceleration
Projectile motion
Rectangular
coordinates
Normal and
tangential
coordinates
Translation
(θ = constant)
Dependent
motion
Define position vectors and
differentiate
Polar
coordinates
Fixed axis
rotation
r
r
dQ
dQ
r r
=
+ ω× Q
dt
OXY dt Oxy
General
plane
motion
Translation
+
Rotation
Rotating
axis
Figure 1.5 Concept Map for Kinematics
In this text, every time we introduce a new concept in kinematics, a reduced version
of this concept map will be included to help you see where the topic fits into the
scheme of things. The reduced version of the concept map is shown to the left and
a more complete version (including equations to be derived later in the course) is
shown on the following page. I would mark the following page in the text if I
were you, because it contains a lot of information we will use in this book. It may
not make any sense right now, but it will as you progress through the book.
1–1
Kinematics
(the geometry of the motion)
Dependent motion
1) Define position vectors
2) Write a constraint equation
(length of cable, for example)
3) Differentiate to get an equation
that relates the
velocities/accelerations
Basic kinematic relationships
r
r
r dθ
r dr
ω=
v=
dt
dt
r
r
r dv
r dω
a=
α=
dt
dt
Relative motion notation
r
r
r
rA = rB + rA / B
r
r
r
vA = vB + vA/B
v
v
v
aA = aB + aA/B
Separate variables and
integrate
Acceleration not constant
dv
a(t): use a =
dt
dv
a(x): use a = v
dx
Use analogous expressions for α(θ), α(t)
Rectangular
Coordinates
r
v = v x ˆi + v y ˆj ,
r
a = a x ˆi + a y ˆj
Constant acceleration
1
x = x 0 + v 0 t + at 2
2
v = v 0 + at
v 2 = v 02 + 2a ( x − x 0 )
(there are analogous
expressions for α,ω,θ and t)
Projectile Motion
x-direction: x = x 0 + v 0 x t , v 0 = v 0 x
y-direction:
y = y 0 + v 0 y t − 12 gt 2 , v y = v 0 y − gt , v 2y = v 02 y − 2g (y − y 0 )
Represent in different
coordinate systems
Normal and Tangential
Coordinates
r
v = veˆ t ,
r
v2
eˆ n
a = v& eˆ t +
ρ
Translation
(θ = constant)
v A = vB
aA = aB
Define position vectors and
differentiate
Polar Coordinates
r
v = r&eˆ r + rθ& eˆθ
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆθ
(
) (
r
r
r r
dQ
dQ
=
+ ω× Q
dt OXY
dt Oxy
(Q is any vector)
)
Fixed Axis Rotation
r r
r
v p = ω × rp / o (Magnitude is ωr, direction is
perpendicular to r)
r
r r
r r r
a p = α × rp / o + ω × ω × rp / o
(
)
General Plane
Motion
= αr perpendicular to r and
ω2r directed from p to the fixed point O
General Plane Motion (translation+rotation)
r
r
r
vA = vB + vA / B
r r
r
= v B + ω × rA / B
r
r
r
aA = aB + aA / B
r
r r
r r r
= a B + α × rA / B + ω × (ω × rA / B )
r
r r
r
= a B + α × rA / B − ω2AB (rA / B )
General Plane Motion (rotating axis)
r r
r
r
r
v p = v o + v rel + ω × rp / o
r
r
r
r r
r r r
r r
a p = a o + a rel + α × rp / o + ω × ω × rp / o + 2ω × v rel
(
)
1–15
1.3 The general problem solving methodology
In this book we will be focusing on problem formulation. Never, ever say “I can’t
find the right equation”. Blah! You should be saying “What principle should I be
using?” I am going to assume that you have some sort of computer algebra
program available to use such as Mathematica, Maple, or Mathcad. If you don’t,
you can still solve most of the problems in this book by hand, but some of them
will involve quite a lot of algebra.
Essential Steps in Problem
Solving:
1. Define your system
2. State the principle
3. Keep track of your
unknowns and equations
To focus on the basic principles (not just looking for an equation) and the
derivation of the governing equations, we will, in general, formulate all the
necessary equations prior to attempting the mathematical manipulations required to
get a numerical answer. In addition teaching you dynamics, one of my goals for
this book is that it will help you become a better problem solver. As a result, when
solving example problems I will try to clearly explain the thought process you
should go through. For example, you should clearly state what your system is,
what principle you are using and you must keep track of your unknowns and
equations.
To accomplish this last task, I encourage you to use an
“unknowns/equations” table in which you list the unknown quantities and keep
track of the number of equations you have. You should not proceed to a numerical
solution until you have enough equations. After the governing equations are
derived, you can then solve the resulting equations using Maple or by hand. An
example of an exam problem I have given in the past and a hand written solution is
shown in Figure 1.6.
Because Maple enables you to solve sets of equations in terms of parameters and to
easily integrate differential equations, we will also occasionally look at the time
response of a system and have you plot the response as a function of time or as a
function of one of the system parameters.
1–16
Figure 1.6 – Sample test problem illustrating the “set-up but don’t solve” methodology.
Chapter 2 Review of Conservation Principles
and Basic Kinematics
In this chapter I will introduce you to some basic kinematics and to the
conservation principles that we will use throughout this book. Specifically, we will
use conservation of linear momentum (both rate and finite time forms), angular
momentum (just a bit) and conservation of energy. Most of these concepts should
be familiar to you from physics so much of this chapter may be a review and
therefore may be skipped. I would recommend, however, that you read Section 2.6
for a summary of the principles and how we will be applying them in this book.
2–2
2.1 Basic Kinematics
In this section we will be discussing some basic particle kinematics. Please note
the figure directly to the left of this paragraph. The shaded boxes correspond to the
parts of the kinematics concept map (presented in Section 1.2 - remember, you
were supposed to mark the page!) that I will be discussing in this section. As
mentioned in Chapter 1, kinematics is the “geometry of the motion.” We don’t
care what is causing the motion; we just want to describe it. How do we describe
motion? From physics, you know the way to describe the motion of a particle is in
terms of quantities such as position, velocity and acceleration.
The topics from the kinematics
concept map covered in this
section are shaded.
In this chapter we will be focusing on the motion of particles. The first thing to
note about a particle is that it is not necessarily small, although it might be. All I
mean when I refer to an object as a particle is that we can neglect any rotation of
the object about its own center of gravity. For example, an airplane can be
considered to be a particle if the radius of curvature of its path is sufficiently large.
The basic kinematic relationships between position, velocity and acceleration are
shown in Table 2.1.
Table 2.1 - Summary of Basic Kinematic Relationships
Variable
Position
Symbol
r
v
x (or r )
Velocity
r
v
Acceleration
r
a
Kinematic Relationship
r
r dx
v=
dt
r
r
r dv d 2 x
= 2
a=
dt dt
Units
m or ft
(2.1)
m/s or ft/s
(2.2)
m/s2 or ft/s2
It is important to note that these quantities are vectors and therefore have a
r
magnitude and a direction. For example, an acceleration of a = -4 ft/s2 means that
the object is accelerating in the opposite direction to whatever I defined to be
positive. If I defined positive to be in the direction of the velocity, then the particle
would be slowing down at a rate of 4 ft/s2.
I will typically denote a vector with by placing an arrow over it. A quantity
without the arrow means I am only considering the magnitude. One way of using
these kinematic relationships is to separate variables and integrate (we are just
dealing with the magnitudes when we do this). All I mean when I say “separate
variables and integrate” is that you need to do some algebra to collect similar terms.
For example, all the velocity terms on the “dv” side of the equation and all the time
terms on the “dt” side. We’ll do a lot of examples to try to make this clear. If we
have the acceleration as a function of velocity or time we can use Eq. 2.2, but if we
have the acceleration as a function of position we can either write it as a 2nd order
2–3
differential equation, or we can often use the chain rule. The relationship between
acceleration, velocity and time is shown below.
dv
a=
dt
If I were to give you the acceleration as a function of the position, x, then you
couldn’t separate and integrate since you don’t have a “dx”. How do we get a “dx”
in the problem? Multiply top and bottom by dx! This is the same as multiplying
the equation by 1.
dv dx dx dv
a=
=
dt dx dt dx
Using Eq. 2.1 we finally get
dv
(2.3)
a=v
dx
In Table 2.2 are shown four common cases where Eqs. 2.2-2.3 are used.
Table 2.2 - Four cases of using the kinematic relationships to separate variables and integrate
Case
1) a = f(t)
Integrate the following
dv
Use Eq. (2.2): a = f ( t ) =
dt
separating variables
v
∫
t
t0
a = f (x) = v
Eq. (2.3)
2) a = f(x)
v(t)
∫
dv = f ( t )dt
v0
gives
dv
dx
separating variables
v
x
v0
x0
Comments
I know it is sloppy to use “v” as a limit in
the integral as well as the integration
variable. I’m assuming that none of you
are picky mathematicians (not that there is
anything wrong with that), and that you
have the maturity to handle it.
v(x)
∫ vdv = ∫ f (x)dx
a = f ( v) =
Eq. (2.2)
dv
dt
v(t)
separating variables
t
v
0
v0
dv
∫ dt = ∫ f (v)
3) a = f(v)
or
Use Eq. (2.3)
a = f ( v) = v
separating variables gives
x
v
x0
v0
v
∫ dx = ∫ f (v)dv
dv
dx
v(x)
When you are given the acceleration as a
function of velocity, you can use either
Eq. 2.2 or Eq. 2.3, depending on what you
want to find.
2–4
4) a = constant
a = f (t ) =
dv
dt
a = f ( v) = v
v(t)
dv
dx
v(x)
v = v 0 + at
v 2 = v 02 + 2a ( x − x 0 )
to find position
v=
dx
dt
x(t)
x = x 0 + v0t +
1 2
at
2
These are the familiar equations from Physics. Note:
These are only valid for CONSTANT acceleration.
Example 2/1 Illustration of Case 1 in Table 2.2
The motion of a particle is found to be given by a = t2. At t = 0 the velocity is v = v0. Find an equation for the velocity as a function of
time.
Strategy: Since we are given the acceleration as a function of time and we want to find the velocity, we need to use the kinematic
relationship between these quantities as given by Eq. 2.2 and we need to separate variables and integrate.
a=
dv
= t2
dt
Separating variables we get
dv = t 2 dt
Integrating we get
v
∫
vo
t
∫
dv = t 2 dt
0
v − vo =
1 3
t
3
v = vo +
1 3
t
3
Solving for v we get
2–5
Example 2/2 Illustration of Case 2 in Table 2.2.
The motion of a particle is found to be given by a = x2 . At x = x0 the velocity is v = v0. Find an equation for the velocity as a function
of x.
Strategy: Since we are given the acceleration as a function of position and we want to find the velocity as a function of position, we
need to use the kinematic relationship between these quantities as given by Eq. 2.3 and we need to separate variables and integrate.
a=
dv dx
dv
=v
= x2
dt dx
dx
Separating variables we get
vdv = x 2 dx
Integrating we get
v
∫
x
vdv =
vo
∫x
2
dx
xo
1 2
v
2
v
vo
1
= x3
3
x
xo
1 2 1 2 1 3 1 3
v − vo = x − x o
2
2
3
3
Finally, solving for v we get
v = v o2 +
2 3 2 3
x − xo
3
3
What if I had asked you for the velocity as a function of time? Clearly we cannot use a = dv/dt since we do not have the acceleration as
a function of time. We have two choices. First, we could use the kinematic relationship between position, acceleration and time as
shown below.
a = x2 =
d2x
dt 2
→
d2x
dt 2
− x2 = 0
which is a 2nd order nonlinear differential equation that we could solve for x(t) which we could then differentiate to find v(t) (or we can
just plug it into the equation we found above for v(x). Alternatively, we can integrate the velocity equation we found above for v(x) to
find x(t) using
v=
2
2
dx
= v o2 + x 3 − x 3o
3
3
dt
Separating variables we get
x
∫
xo
dx
v o2 +
2 3 2 3
x − xo
3
3
t
∫
= dt
0
Unfortunately for us, this is not a very easy integral to do. Using Maple, I got about a page of output and the solution was in terms of
elliptic integrals, that is, t(x). It wouldn’t even solve for x(t). Thus, the best way to solve the problem would probably be numerically,
which means I would need to give you v0 and x0. For example, if x0 = 4 and v0 = -11 (I just pulled these out of the air) then if we solve
for x(t) numerically we get
2–6
I only plotted out to t = 3 because the plot blows up quickly thereafter.
Example 2/3 Illustration of Case 3 in Table 2.2
The motion of a particle is found to be given by a = v2.
a) Find an equation for the velocity as a function of time if at t = 0 the velocity is v = v0.
b) Find an equation for the velocity as a function of position if at x = x0 the velocity is v = v0. .
Strategy: Once again, this is a pure kinematics problem. For part a) we will need to use the kinematic relationship between
acceleration, velocity and time and for part b) we will need to use the one that relates acceleration, velocity and position. Since the
procedure is identical, I will solve parts a) and b) in parallel.
a)
b)
dv
a=v =
dt
2
Separate variables
a = v2 =
dv dx
dv
=v
dt dx
dx
Separate variables
dv
v
2
dv
= dx
v
= dt
Integrate
Integrate
v
t
dv
∫ v = ∫ dt
2
vo
−
0
1
v
v
=t
vo
1 1
− −
v vo
=t
Solving for v we get
vo
v=
1− vo t
v
∫
vo
dv
=
v
l n ( v)
v
vo
x
∫ dx
xo
x
=xx
o
ln( v) − ln( v o ) = x − x o
v
ln
vo
= x − xo
Solving for v we get
v = v o e (x − x o )
Note: This is clearly only valid for v/vo > 0.
A graphical interpretation of the relationship between position, velocity and
acceleration is shown in Figure 2.1. Given the position curve shown on the top of
Figure 2.1, we can get the velocity curve because we know v = dx/dt, that is, the
velocity is simply the slope of the displacement verses time curve. Clearly when
2–7
Acceleration
Velocity
Position
the slope is zero the velocity is zero (t = 0, t = 4). The velocity will be a maximum
at a point of inflection, in this case when t = 2. This is all basic calculus so I won’t
spend any more time discussing it in this book.
40
20
0
-20
-40
-60
0
1
2
3
4
T ime (s)
5
6
7
0
1
2
3
4
T ime (s)
5
6
7
0
1
2
3
4
T ime (s)
5
6
7
40
20
0
-20
-40
-60
40
20
0
-20
-40
-60
Figure 2.1 – Position, velocity and acceleration graphs
2.2 Conservation of Linear Momentum (general comments)
To begin our discussion of linear momentum I will use the same approach used in
Basic Engineering Science - A Systems, Accounting and Modeling Approach by
Don Richards. In fact, I will follow his development very closely. Let’s start by
addressing four questions we can ask ourselves when discussing any extensive
properties. These questions are:
1. What is linear momentum?
2. How do you calculate it?
3. How can it be transported?
4. How can it be created or destroyed?
Path of particle
What is linear momentum?
y
r
r
r
For a particle of mass m and velocity v , as shown in the Figure 2.2, the linear
momentum of the particle is
r
r
P = mv
(2.4)
P
r
v
x
z
Figure 2.2 - A particle
traveling through space
It is important to note that linear momentum is a vector, that is, it has a magnitude
and a direction. The direction of linear momentum will be in the same direction as
2–8
the velocity vector. The units of linear momentum are kg-m/s in SI and slug-ft/s in
English units.
The velocity vector can be related to the position vector using basic kinematic
r
relationships presented Section 2.1. If we write the position vector, r , in terms of
rectangular coordinates we get
v
r = xˆi + yˆj + zkˆ
(2.5)
where ˆi , ˆj, and kˆ are unit vectors in the x, y and z directions respectively. Eq. 2.5
can easily be differentiated to obtain the velocity vector
r
r dr
v=
dt
dx ˆ dy ˆ dz ˆ
=
i+
j+ k
dt
dt
dt
ˆ
ˆ
= v i + v j + v kˆ
x
y
(2.6)
z
It is important to note that the velocity must be measured relative to some point.
Conservation of linear momentum uses the absolute velocity, so the velocity should
be measured relative to an inertial reference frame. For our purposes this means
a coordinate system that is not rotating or accelerating with respect to the earth, i.e.
an earth-fixed coordinate system. For motion of spacecraft you would need to use
a sun-centered, non-rotating reference frame.
Linear
What type of property is linear momentum, intensive or extensive?
momentum is an extensive property, meaning it depends on the extent of the
system. From the definition of linear momentum, we can think of velocity in
slightly different terms. From Eq. 2.4 we find
linear momentum
v
v = velocity =
unit mass
Therefore, velocity is an intensive property, that is, it has a value at a point.
How do you calculate the linear momentum of a system of
particles?
For a system of particles, the linear momentum can be determined by adding up the
momentum for each mass,
# of
particles
∑m v
v
p sys =
i
r
i
(2.7)
i =1
For a continuous system this summation can be changed to an integral over the
volume of the system
r
p sys =
r
r
∫ vdm = ∫ vρd∀
m sys
∀
(2.8)
2–9
y
where ρ is the density and ∀ is the volume. We really don’t want to perform the
integral given by Eq. 2.8 if we don’t have to. How do we avoid this? Simple. By
introducing the concept of the center of mass. The center of mass for a system is
often labeled as G or CG as shown in Figure 2.3. The definition for the center of
mass is
r
r ρd∀
r
(2.9)
rG = ∀
ρd∀
∫
G
∫
z
∀
x
∫
where ρd∀ is simply the total mass of the system, msys. If the density is uniform
∀
Figure 2.3 - Center of mass
then Eq. 2.9 reduces to
r
1 r
rG =
r d∀
∀
∫
(2.10)
∀
How does this help us? The center of mass can help simplify the linear momentum
equations. From Eq. 2.9 we see that
r
r
∫ rρd∀ = r ∫ ρd∀
G
∀
∀
or if we take the derivative with respect to time (assuming the density and volume
are not functions of time)
r
r
r
∫ vρd∀ = v ∫ ρd∀ = v
G
∀
so
G m sys
∀
r
r
r
Psys = vρd∀ ≡ m sys v G
∫
(2.11)
r
where v G is the velocity of the center of mass.
How can linear momentum be transported?
There are primarily two mechanisms by which momentum can be transported: with
mass and by forces. Let’s first talk about forces. Forces can be separated into two
categories as shown in Figure 2.4, contact forces and body forces.
External Forces
Surface
Normal
Body
Shear
Gravity
Electrostatic
Force
key: Force Field
key: Contact
Figure 2.4 - Break down of forces
etc.
2–10
A body force always acts in a distributed fashion within the volume of the system
and is the result of placing the system in a force field such as a gravitational field,
electric field, magnetic field, etc. The only body force we will use in this text is the
force exerted by the earth on a mass placed in the earth's gravitational field. We
call this force, weight. Although this force acts throughout the system, its effect is
identical to that of a concentrated force acting at a specified point within the
system. The magnitude of the gravitational force is the mass times the local
gravitational constant (which we will usually assume to be 9.81 m/s2 or 32.2 ft/s2
unless otherwise noted), that is msysg. This force is defined to act at the object’s
center of gravity.
Surface forces are external forces that act at the boundary of a system. For this
reason, they are also called contact forces. Figure 2.5 shows how any contact force
can be resolved into normal and shear components. The normal component is
perpendicular to the surface of contact and the shear component is parallel to it.
mg
Isolate the box
(i.e. draw a free
body diagram)
v
R = Total contact
force on box
surface with
friction
mg
R can be resolved
into components
Rx = Shear Force
Ry, Normal Force
Ry
The ground has an
equal and opposite
contact force, R
Rx
Figure 2.5 - Any contact force can be resolved into a shear and normal component.
nˆ
dA
r
v
I’d like to say a few more words about the transport of linear momentum with
mass. From the definition of linear momentum, it is clear that any mass that has a
velocity will have linear momentum. Therefore, when mass enters a system it will
carry with it its own linear momentum. The rate of transport of linear momentum
with mass is equal to the mass flow rate times the local velocity at the boundary
r
& v . When the velocity is not spatially
(assuming the velocity is uniform), that is, m
uniform at the flow boundary, the formula is a bit more complicated because we
need to use Figure 2.6 and to integrate over the area as shown below
r
r
& dA
Pdue to mass transport = vm
∫
A
=
r
r
∫ (v)(ρv
rel
⋅ nˆ )dA
(2.12)
A
Figure 2.6 - Mass transport of
linear momentum at a boundary
=
r
∫ (v)(ρv )dA
rel n
A
r
where v is the local velocity vector measured with respect to an inertial reference
r
frame, v rel is the local velocity vector measured with respect to the surface through
2–11
which the mass is entering the system, and nˆ is a unit vector perpendicular to the
differential surface area dA and pointing out of the system. All the dot product
r
does is take the component of v rel in the direction of nˆ which I called v reln . The
main point of showing you Eq. 2.12 (since we will never need to do the integral in
this class) is so that you will recognize that the mass flow rate depends on the
relative velocity. If the flow is one-dimensional then the mass flow rate is
& = ρv rel A
m
(2.13)
and the linear momentum transported by mass can be written as
r
r
Pdue to mass transport = (ρv rel A) v
The net transport of linear momentum with mass can be determined by summing
the transports over all the inlets and outlets of the system:
Net transport rate of linear momentum
=
into the system with mass flow
∑ m& v − ∑ m&
i
in
r
i
r
ovo
out
How can linear momentum be generated or destroyed?
It can’t! Linear momentum is conserved. The basis for this conclusion is years of
empirical evidence.
Finally, the rate form for conservation of linear momentum can be written as
Net rate of transport Net rate of transport
Rate of accumulati on
of linear momentum = of linear momentum + of linear momentum
into the system by
into the system by
inside system at time t
external forces at time t mass flow at time t
or in terms of symbols, conservation of linear momentum (rate form) becomes
Important Equation!
Conservation of
Linear Momentum
(rate form)
r
dPsys
dt
=
r
∑ F +∑ m& v −∑ m&
r
i i
in
r
o vo
(2.14)
out
where
r
r
Psys = mvG = linear momentum of the system. For a system containing several
r
objects Psys =
n
∑ (mv
r
G )i
i =1
m = mass of the system
r
v G = velocity of the center of gravity
r
F = external forces
& i = mass flow entering the system
m
r
v i = velocity of mass entering the system
2–12
& o = mass flow exiting the system
m
r
vo = velocity of mass exiting the system
r
& i vi = rate of momentum transfer into the system by mass flow
m
r
& o vo = rate of momentum transfer out of the system by mass flow
m
In words, the finite time statement of conservation of linear momentum is
LM inside
system
at time t 2
LM inside
− system
at time t 1
Net amount of LM
Net amount of LM
= transporte d into system + transporte d into system
by ext. forces during the by mass flow during the
time period ∆t
time period ∆t
or in equation form
Important Equation!
Conservation of
Linear Momentum
(finite time form)
r
∆Psys =
t2
∫∑
t1
t
2
r
Fdt + (
∫∑
t2
∫ ∑ m&
r
& i v i )dt − (
m
in
t1
t1
r
o v o )dt
(2.15)
out
In the next few sections we’ll take a look at how to apply these principles.
2.3 Conservation of Linear Momentum (Rate Form)
As shown in the previous section the rate form of conservation of linear momentum
is:
r
r
dPsys
r
r
& i vi − m
& o vo
=
F+ m
dt
in
out
∑ ∑
Important Equation!
Conservation of
Linear Momentum
for a closed system
(rate form)
∑
which is valid for both an open system and a closed system. Let’s see how this
reduces to Newton’s 2nd Law. If we assume a closed system, that is, no mass flow
into or out of the system then Eq. 2.14 reduces to
r
dPsys
r
=
∑F
=
∑F
(2.16)
r
In fact, let’s just look at a single particle, so Psys = mv where m is the mass of the
dt
particle. Therefore
r
dPsys
r
dt
r
d(mv) r
= Fnet
dt
where I have defined the sum of the forces to be the net force acting on the system.
Since the mass is a constant we can pull it outside the derivative and then use the
kinematic relationship between position, velocity and time resulting in the
following
2–13
r
dv r
= Fnet
m
dt
r
r
ma = Fnet
which is Newton’s 2nd Law. Therefore, the rate form of conservation of linear
momentum for a closed system is Newton’s 2nd law.
How do we apply this principle and when should we use it? This principle is useful
when you want to find the differential equations governing the motion of an object,
the acceleration at an instant, contact forces, etc. If you want to find the velocity or
position of an object you will have to integrate the acceleration (or solve the
differential equation). One key step I will emphasize throughout this book when
applying Newton’s 2nd Law is the importance of drawing a free body diagram,
FBD. Guidelines for drawing a free body diagram are found below.
Guidelines for Drawing a Free Body Diagram*
1.
2.
3.
4.
5.
6.
Select a system. Every system can be broken down into smaller subsystems. For a given
problem, there may be several possible systems and different questions may require a
different system.
Sketch the physical object clearly identifying the boundaries of your system. This is
usually done with a dashed line to indicate the system boundary.
Detach the system from its surroundings and sketch the isolated contour of the
system, i.e. the system boundaries.
Identify the external forces acting between the system and the surroundings. Only
consider the forces exerted by the surroundings on the system. Remember that there are
two types of external forces: contact (or surface) forces that act on the boundaries of the
system and body forces produced by fields such as the gravitational force commonly
called weight.
For each force, draw an arrow on the system diagram showing the direction and
location of the force. Care should be taken to draw each arrow with the correct
direction (line-of-action and sense) and position. Label all forces with a name, number,
or symbol. Draw the vector on the diagram by placing either the tail or the head of the
arrow at the point of application:
• Contact forces should be applied at the appropriate point on the system boundary
where the system was detached from the surroundings.
• The weight vector should be applied at the center of gravity of the body.
• If you do not know the correct direction of a force, assume a direction. If your
analysis results in a negative numerical value, then the actual direction is opposite
to the direction assumed.
Draw a coordinate system and indicate all pertinent dimensions and angles on the
free body diagram.
* Modified from Basic Engineering Science - A Systems, Accounting and Modeling
Approach by Don Richards.
2–14
2.3.1 Procedure for applying the rate form of
conservation of linear momentum (Newton’s 2nd law) to
particles
When should you use this principle? When you want to find forces and/or
accelerations. You can also use this principle to find velocities and distances, but
first you will need to find the accelerations and then to integrate. After deciding
that you should use the rate form of conservation of linear momentum to solve a
problem (we usually don’t use angular momentum for particles) what do you do?
The following procedure is intended to give you a methodic approach when solving
problems of this type. Don’t try to use your intuition or to skip steps. Good
engineering communication requires you to show all of your work and for it to be
neat and organized so that it is easy for someone else to understand what you are
doing. This includes drawing figures and stating what you are doing.
1.
Kinetic
Diagram (KD)
Free Body
Diagram (FBD)
2.
3.
ma G 2
F2
W
4.
F1
5.
Identify the system. The system you pick usually involves the forces and/or
accelerations in the find statement.
Draw the free body diagram (FBD). Include all external forces and moments.
Don’t forget gravity.
Draw the kinetic diagram (KD). On this diagram you put all of the mass times
acceleration terms. For simple rectilinear problems it is OK to skip this step,
but when we get to curvilinear motion and rigid body motion we will discuss
r
the kinetic diagram in more detail. For plane motion be sure to include ma G .
r
The constraints on the problem may permit you to limit the direction of a .
Place a coordinate system between the FBD and KD to be used when applying
conservation of linear momentum.
Apply the scalar equations for conservation of linear and angular momentum to
the FBD and KD. Be sure to define a positive direction for the summations.
dPsys x
dt
6.
=
∑F
,
x
dPsys y
dt
=
∑F
y
Solve the equations for the required unknowns. If the two scalar equations
have more than two unknowns then a kinematic analysis may be required for
the problem solution. If you still need more equations after a kinematic
analysis, then try another FBD/KD of an interrelated system.
Example 2/4
A jet engine is attached to a stationary test stand to measure
its thrust as shown in the figure. The steady-state mass flow
rate through the engine is 60 kg/s. The inlet air velocity is 100 ft/s
and the inlet area is 0.3 m2. The exit velocity is 1000 m/s and the
exit area is 0.25 m2.
Jet
Engine
Rx
Determine the value of the test stand horizontal reaction force, Rx .
Strategy: Since we want to determine the reaction force, we will need to use conservation of linear momentum.
r
dPsys
dt
=
r
∑ F +∑ m& v −∑ m&
r
i i
in
out
r
o vo
2–15
Since the stand is not moving, the left hand side of this equation will be zero. We won’t be doing many static problems in this book, but
I’ve included a few just so you can see how the momentum transported by mass works. Since this is a vector equation, let’s draw a
couple of pictures, a free-body diagram (FBD) for the external forces and a mass-flow diagram (MFD) for the mass flow terms.
FBD
MFD
mg
& vi
m
Jet
Engine
& ve
m
Rx
Ry
We only want the horizontal reaction force, so by applying conservation of linear momentum in the x-direction (positive to the right) we
get:
& vi − m
& ve
0 = Rx +m
Solving for Rx we get
& ve − m
& vi
Rx = m
= (60 kg/s)(1000 m/s) - (60 kg/s)(100 m/s)
= 54,000 N
So the final answer is Rx = 54,000 N to the right. How would your answer change if there were
some sort of flow diverter at the outlet to the nozzle as shown to the right. In this case, there is no
component of the flow exiting the system in the x-direction, so all we get is
MFD
& ve
m
& vi
m
& vi
Rx = 0−m
= 0 - (60 kg/s)(100 m/s)
= -6000 N
so the force is now acting to the left instead of to the right. What if the bend made a 180° turn and
not just 90°? In this case when we apply linear momentum in the x-direction we get
& v i − (−m
& ve )
0 = Rx +m
MFD
& ve
m
& vi
m
& vi − m
& v e = −66000 N
→ R x = − m
A type of problem you are most likely familiar with from physics is projectile
motion. Let’s look at an example to make sure you remember how to do this type
of problem.
2–16
Example 2/5
A ball is thrown with a speed of 40 ft/s at an angle θ with respect
to the horizontal. Assume the ball is released from a height of 6 feet
off of the ground.
a) If α = 30° and θ = 45°, determine the distance the ball travels
down the hill.
b) If α = 30°, the angle the ball should be thrown at, θ, to maximize
the distance the ball travels down the hill before it hits the ground.
c) Does your answer make sense? What if α = 0?
v
θ
α
Strategy: Since we have forces acting on the ball (gravity), we need to use conservation of linear momentum. At this point, I don’t want
you to use the “projectile motion equations” that you have seen in physics. Let’s solve the problem starting with our basic principles to
derive the projectile motion equations just so you are confident as to where they come from and the assumptions they have behind them.
For our system, let’s pick the ball. This is a closed system, so we won’t have any mass flow coming into or out of our system, so our
basic principle is:
r
dPsys
dt
=
r
∑F
The free body diagram for our system is shown to the right. We are obviously assuming no air
resistance in the problem. Applying linear momentum in the x and y directions we get:
y
FBD
x
LM x-direction (+→)
dPx
=
dt
∑F
x
→ ma x = 0
→ a x = 0
mg
LM y-direction (+↑)
dPy
dt
=
∑F
y
→
ma y = −mg
→ a y = −g
So, from linear momentum we find that the acceleration in the horizontal direction is zero and in the vertical direction is -g. Since we
want to find out how far the ball travels, and then to find the angle to maximize this distance, we need an equation for the position. How
do we get this? Use our kinematics to integrate our acceleration (or use the constant acceleration equations, but let’s do the integration
because it is so fun!)
We’ll do the y-direction first.
ay =
dv y
dt
variables
separate
→ dv y = a y dt
Integrating we get
∫
vy
vo y
∫
t
dv y = a y dt
0
v y − v oy = a y t
→
v y = v oy + a y t
→ v y = v o y − gt
Using the kinematic relationship between velocity, position and time we can integrate again.
2–17
∫
y
yo
∫
t
dy = v y dt =
0
y − y o = v oy t +
t
∫ (v
0
oy
1
ayt2
2
+ a y t )dt
→
y = y o + v oy t +
1
ayt2
2
→
y = y o + v oy t −
1 2
gt
2
So, we now have an equation for the position in the y-direction. It turns out that we can do exactly the same thing in the x-direction and
we will get
v x = v x o (the velocity in the x-direction is a constant since there are no forces in that direction)
x = x o + v ox t
y
All we have done so far is to derive the projectile motion
equations (these were also given to you in the concept map
presented in Chapter 1). Now you may be asking yourself,
“Do I have to go through all this trouble every time?” The
answer is, “No, you do not.” I did want to show you the
derivation once, but if you have projectile motion, that is, the
only force acting on the particle is gravity, you can go
straight to the kinematic equations for position and velocity.
Now let’s solve our problem.
vo
θ
x
6 ft
yf
α
Let’s define our coordinate system and unknowns as shown
in the figure. From the figure to the right we see that:
xo = 0
yo = 6 ft
v o x = v o cos θ
v o y = v o sin θ
xf
Using our projectile motion equations we get
x f = ( v o cos θ) t f
y f = 6 + ( v o sin θ) t f −
1 2
gt f
2
(1)
(2)
If we assume that we know θ, then we have 3 unknowns: the final position, xf and yf, and the final time, tf. How do we get more
equations? Well, we know that the ball hits the ground, so we have a relationship between xf and yf as shown below.
tan α =
yf
xf
(3)
Finally, the distance traveled down the hill is
d = x f2 + y f2
We now have 4 equations and 4 unknowns (xf, yf, tf, d) that we can solve either by hand or using Maple. A Maple printout is shown
below.
(4)
2–18
So the answer for part a) is d = 35.46 ft. To solve part b) we will use the same equations (1-4) but solve for d (in the Maple code I call it
“dist”) in terms of θ. To maximize this we just need to take the derivative and set it equal to zero. Conceptually, this is very easy, but it
turns out that the algebra is quite messy. The Maple printout to solve this problem is shown below just so you have an appreciation for
how hard it would be to solve this problem by hand. Feel free to just to the answer at the bottom of it.
Part b)
> alpha:=30*Pi/180:
> g:=32.2:
> v0:=40:
> eq1:=xf=v0*cos(theta)*tf;
> eq2:=yf=6+v0*sin(theta)*tf-1/2*g*tf^2;
> eq3:=tan(alpha)=yf/xf;
> eq4:=dist2=sqrt(xf^2+yf^2);
eq1 := xf = 40 cos ( θ ) tf
eq2 := yf = 6 + 40 sin( θ ) tf − 16.10000000 tf 2
1
yf
eq3 :=
3=
3
xf
eq4 := dist2 = xf2 + yf2
> sol1:=evalf(allvalues(solve({eq1,eq2,eq3,eq4},{xf,yf,tf,dist2})));
sol1 := { xf = 40. cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ), tf =
−.7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. , dist2 =
46.18802154 cos ( θ ) ( − .7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ), yf =
23.09401077 cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ) }, { tf =
−.7172053034 cos ( θ ) + 1.242236025 sin( θ )
− .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. , dist2 =
2–19
46.18802154 cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
− .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ), yf =
23.09401077 cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
− .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ), xf = 40.
cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
− .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ) }
We have two solutions here, so let's pull out the positive value of the distance
> Dist1:=subs(sol1[1],dist2);
Dist1 := 46.18802154 cos ( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. )
Take the derivative and set it equal to zero
> eq2:=diff(Dist1,theta)=0;
eq2 := −46.18802154 sin( θ ) ( −.7172053034 cos ( θ ) + 1.242236025 sin( θ )
+ .004140786749 30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735. ) +
46.18802154 cos ( θ ) .7172053034 sin( θ ) + 1.242236025 cos ( θ )
.002070393374 ( 120000. cos ( θ ) sin( θ ) + 103923.0485 sin( θ ) 2 − 103923.0485 cos( θ ) 2 )
=0
+
30000. cos ( θ ) 2 − 103923.0485 cos ( θ ) sin( θ ) + 90000. sin( θ ) 2 + 21735.
Solve for theta to maximize the distance
> sol2:=solve(eq2);
sol2 := -1.303738877 + 5.466783766 I, .9752808912, 2.642002898, .2670741009 + 5.466794214 I,
-1.303738877 − 5.466783766 I, .2670741009 − 5.466794214 I
We know the angle needs to be less than 90 degrees (otherwise she is throwing
backwards) so let's choose .975 and convert to degrees.
> theta2:=evalf(sol2[2]*180/Pi);
θ2 := 55.87947889
Therefore, the angle to maximize the distance is θ = 55.88° for α = 30°. It turns out that this is a relatively hard problem even if α = 0°.
When you substitute α = 0° into the Maple worksheet shown above you get θ = 41.9°. Now some of you may be thinking, “I thought
you were suppose to throw something at 45° to maximize the distance! I’m confused.” It turns out that θ = 45° give you a maximum
distance only when yo = 0.
How could we make this problem even more difficult? Easy, just add air resistance. In that case we will no longer have constant
accelerations. If we assume the air resistance is proportional to the square of the speed with a constant of proportionality equal to D,
then at any instant the resisting force will oppose the motion as shown below.
v
θ
Dv2
θ
Therefore, the force in the x and y directions will be
Fx = − Dv 2 cos θ = − Dv x v = −Dv x v 2x + v 2y
Fy = − Dv 2 sin θ = −Dv y v = − Dv y v 2x + v 2y
The FBD for this problem is shown to the right. Applying linear momentum in
the x and y directions we get:
Dv y v 2x + v 2y
FBD
Dv x v 2x + v 2y
y
x
mg
2–20
LM x-direction (+ →)
dPx
=
dt
∑F
x
→ ma x = −Dv x v 2x + v 2y
→
dv x
= − Dv x v 2x + v 2y
dt
(1b)
LM y-direction (+↑)
dPy
dt
=
∑F
y
→ ma y = − mg − Dv y v 2x + v 2y
→
dv y
dt
= − mg − Dv y v 2x + v 2y
(2b)
We now have two coupled non-linear first order differential equations which are not easy to solve. We can write the kinematic
relationships for the positions as well, giving us two more equations:
vx =
dx
dt
(3b)
vy =
dy
dt
(4b)
We now have 4 equations, granted they are differential equations, but we can solve them for x, y, vx and vy. I solved these numerically
in Maple and have included the printout below along with a plot of the trajectory of the ball using a 0.25 lbf ball and a damping of D =
0.001 lbf/(ft/s)2.
> with(plots):
> m:=0.25/32.2;
> g:=32.2;
> damp:=.001;
m := .007763975155
g := 32.2
damp := .001
> eq1:=m*diff(vx(t),t)=-damp*vx(t)*sqrt(vx(t)^2+vy(t)^2);
∂
eq1 := .007763975155 vx( t ) = −.001 vx( t ) vx( t ) 2 + vy( t ) 2
∂
t
> eq2:=m*diff(vy(t),t)=-m*g-damp*vy(t)*sqrt(vx(t)^2+vy(t)^2);
∂
eq2 := .007763975155 vy( t ) = −.2500000000 − .001 vy( t ) vx( t ) 2 + vy( t ) 2
∂t
> eq3:=vx(t)=diff(x(t),t);
eq3 := vx( t ) =
∂
x( t )
∂t
eq4 := vy( t ) =
∂
y( t )
∂t
> eq4:=vy(t)=diff(y(t),t);
> sol1:=dsolve({eq1,eq2,eq3,eq4,x(0)=0,y(0)=6,vx(0)=40*cos(45*Pi/180),
vy(0)=45*sin(45*Pi/180)},{x(t),y(t),vx(t),vy(t)},type=numeric,output=listprocedure);
sol1 := [ t = ( proc (t) ... end proc ), x( t ) = ( proc (t) ... end proc ), y( t ) = ( proc (t) ... end proc ),
vx( t ) = ( proc (t) ... end proc ), vy( t ) = ( proc (t) ... end proc ) ]
> odeplot(sol1,[x(t),y(t)],0..3);
2–21
Example 2/6
A fragile piece of equipment is to be shipped in a container containing packing material. The material can be modeled like a spring as
shown.
Compression, mm
model
Fragile
equipment
Fragile
equipment
Material 2
F = k2y2
Material 1
F = k1y
1.5m
1.5m
Force, N
You have two choices of packing material that have different compression characteristics. The force-deflection characteristics of the
two materials are shown in the figure where k1 = 25 N/mm and k2 = 12.5 N/mm2 and is measured from the point where the spring is
undeflected. The mass of the fragile piece of equipment is 5 kg. Before sending the actual piece of equipment you have been asked to
perform some preliminary calculations assuming the equipment will be dropped from a height of 1.5 m. For the two types of packing
material find:
a) the maximum acceleration the equipment will experience
b) the maximum compression of the packing material
Strategy: There are a couple of preliminary calculations we should start with such as determining the velocity that the package will hit
the ground and the initial compression of the packing material. For the velocity we will just use projectile motion and for the initial
compression we will use linear momentum. Our system will be the fragile package. Finally, for the remainer of the compression we
will use linear momentum (rate).
Initial velocity:
As the box falls, the only force acting on it is gravity, so we can use projectile motion, that is, ay = -g. We need to integrate this to get
the velocity. Since we know the distance the box will travel, we will use the chain rule to get the velocity as a function of displacement.
dv y dy
= −g
dt dy
dv y
= vy
= −g
dy
ay =
∫
v
variables
separate
→ v y dv y = −
0
∫
0
h =1.5
gdy gives
→
1 2
v = gh
2
so the velocity of impact is
v impact = 2gh = 2(9.81m/s 2 )(1.5m) = 5.425 m/s
Now let’s find the initial compression of the two different types of packing material.
mg
Drawing a FBD before the package is dropped we get the figure shown. The package is not accelerating so
dPy
dt
=
∑F
y
→ 0 = mg − Fc
→ Fc = mg
Fc
2–22
Therefore we can determine the initial static deflections for our two materials.
→ y st =
Material 1: k 1 y st = mg
→ y st =
Material 2: k 2 y st2 = mg
mg (5 kg)(9.81 m/s 2 )
=
→ y st = 1.962 mm
k1
25 N/mm
(5 kg)(9.81 m/s 2 )
mg
=
k2
12.5 N/mm 2
→ y st = 1.981 mm
In both cases, the initial compression is about 2 mm. To find the subsequent motion after impact we need to apply conservation of linear
momentum to find the acceleration of the mass. The free body diagram we drew earlier is still valid. The only difference is that the left
hand side of our linear momentum equation will not be zero.
LM y-direction (+↓)
dPy
dt
=
∑F
y
→ ma y = mg − Fc
→ m
dv
= mg − Fc
dt
(1)
I dropped the “y” subscript on v since we are only looking at motion in the y-direction. We now have an equation for the acceleration.
The maximum acceleration will occur when Fc is a maximum, so we need to solve part b) first to find the maximum deflection and then
substitute that deflection into Eq. 1. So how do we find the maximum deflection? We can’t separate variables and integrate Eq. 1 since
Fc is a function of y and we don’t have a dy. We have two options: 1) use v = dy/dt so we have a second order differential equation or
2) use the chain-rule so we can separate variables and integrate. Since we want the maximum displacement, and we don’t really care
about the time it takes to reach that displacement, we’ll do option 2.
m
dv dy
= mg − Fc
dt dy
dv
mv
= mg − Fc
dy
Separating variables we get
v
y
v impact
y st
∫ mvdv = ∫
(mg − Fc )dy
(2)
For material 1 we get
∫
v
mvdv =
v impact
∫
y
y st
(mg − k 1 y)dy
y
1
1
1
2
mv 2 − mv impact
= mgy − k 1 y 2
2
2
2
y st
= mgy − mgy st −
1
1
k 1 y 2 + k 1 y st2
2
2
The maximum displacement will occur when the velocity is zero, so solving Eq. 2 for y after setting v = 0 we get
1
1
1
2
k 1 y 2max − mgy max − k 1 y st2 + mgy st − mv impact
=0
2
2
2
We therefore have a quadratic equation that we need to solve for ymax. This is easy to do by hand, but I used Maple since I am lazy. I’ve
included the printout below. Please note that I’ve converted everything to meters to make sure my units are consistent.
2–23
So ymax = 7.87 cm, which is really quite a large displacement. The maximum acceleration can be found by solving Eq. 1 for the
acceleration giving
a max = g −
k 1 y max
(25,000 N/m)(.07868 m)
= 9.81 m/s 2 −
m
5 kg
= −383.6 m/s 2
which is equal to about 39 g’s. Let’s look at material 2. Substituting into Eq. 2 we get
∫
v
mvdv =
v impact
∫
y
y st
(mg − k 2 y 2 )dy
y
1
1
1
2
mv 2 − mv impact
= mgy − k 1 y 3
2
2
3
yst
1
1
= mgy − mgy st − k 1 y 3 + k 1 y 3st
3
3
To find the maximum displacement, we set v = 0 and solve for y = ymax. We need to solve a cubic equation, which is hard to do by hand
but very easy using Maple. The maximum acceleration can be found by using the maximum displacement and substituting into Eq. 1.
The Maple solution to this part of the problem is shown below.
Therefore, the maximum displacement is 2.62 cm, which is much less than we had before, but the maximum acceleration is 1704 m/s2,
or about 174 g’s. So, there is a tradeoff between the amount of deflection and the maximum acceleration. This problem also illustrates
that when you have shock loading, such as dropping a package on the ground, the accelerations can be very high.
2–24
Example 2/7
The 250-kg lunar lander is descending onto the moon’s surface
with a velocity of 80 m/s when its retro engine is fired. The engine
produces a thrust T as shown. If the lunar lander is to hit the ground
with a velocity less than 0.5 m/s, determine when the thruster should
be fired. How high above the surface of the moon will the lander be?
The gravitational constant on the moon is 1.62 m/s2.
Thrust, N
1000
t, s
2
Strategy: We need to use the rate form of conservation of linear momentum since we have forces involved. Since we are given an intial
velocity, a desired final velocity and a desired distance above the moon we need to use kinematics after we find the acceleration.
Picking the lander as our system we will start by drawing a free body diagram.
mg
LM y-direction (+↑)
dPy
dt
=
∑F
y
→ ma = T − mg
(1)
T
We can also write an equation for the thrust T,
T = 500t t ≤ 2
T = 1000 t > 2
Solving Eq. 1 for the acceleration we get
a=
dv T
= −g
dt m
→
∫
vf
v0
dv =
t
T
∫ m − g dt
(2)
0
Let’s start by finding the velocity of the ship and the distance it has traveled when t = 2 s. Substituting in numbers we get
∫
vf
-80
dv =
∫
2 500 t
0
− 1.62 dt
250
v f + 80 = t 2 − 1.62 t
→ v = t 2 − 1.62 t − 80
Separating variables and integrating again we get and
v=
dy
= t 2 − 1.62 t − 80
→
dt
∫
y
0
dy =
∫ (t
which gives
t3
y = − 0.81t 2 − 80t
3
t
0
2
)
− 1.62 t − 80 dt
2–25
For t = 2 s we get v = 22-1.62(2)-80 = -79.24 m/s and y = 23/3-0.81(22)-80(2) = -160.57 m, so the lander has traveled 160.57 meters in
the first 2 seconds and has a speed of 79.24 m/s towards the surface after 2 s.
For t >2 we have T = 1000 N. Plugging this into Eq. 2 we get
v
t 1000
v1
2
∫ dv = ∫ 250 − 1.62 dt
v − v 1 = 2.38( t − 2)
(3)
→
v = v 1 + 2.38( t − 2)
If we let v1 = -79.24 m/s and v = -0.5 m/s and solve for t we get t = 35.084 s. Therefore, from the time we fire the thrusters until the
module has a velocity of 0.5 m/s down will be 35.084 s. Integrating Eq. 3 we get the displacement to be
v=
dy
= v1 + 2.38( t − 2)
dt
→
∫
y
y1
dy =
t
∫ (v
2
1
+ 2.38( t − 2) ) dt
which gives
t2
y − y 1 = v1 t + 2.38( − 2 t )
2
t
= v1 t + 2.38(
2
t2
t2
− 2 t ) − 2v 1 + 4.76
→ y = y1 + v1 t + 2.38( − 2 t ) − 2v 1 + 4.76
2
2
Substituting in y1 = -160.57 and t = 35.084 s we get
y = -160.57 + (−79.24)(35.084) + 2.38(
(35.084) 2
− 2(35.084)) − 2(−79.24) + 4.76
2
= −1479.6 m
Therefore, the rockets need to be fired when the module is 1479.6 m above the ground and it will take 35.08 seconds from the time the
rockets are fired for the module to strike the ground.
2.3.2 Frictional forces
There are two types of friction, dry friction (coulomb friction) and fluid friction. A
friction force is a shear force generated at the interface of two materials. Friction
models, also called constitutive relations, for dry friction and for viscous friction
are shown in Table 2.3. In this table Ff denotes the friction force.
Table 2.3 - Two Friction Models
Dry Friction
Magnitude depends on the magnitude of
the normal force
Fluid Friction
Magnitude depends on the relative velocity
between the surface and the fluid
Ff = µkN
where
µk = coefficient of kinetic friction
N = normal force
Ff = friction force
Possible models:
Ff = k1v (viscous friction)
Ff = k2v2 (drag)
Direction is in the opposite direction to the
velocity of the object.
Direction is in the opposite direction to the
velocity of the object.
2–26
y
x
System boundary
P
Lets explore dry friction in more detail by considering the object shown in Figure
2.7. A system diagram (free body diagram) showing all linear momentum
interactions with the surroundings is shown in Figure 2.8. Conservation of linear
momentum (closed system) can be written
F
r
dPsys
W
dt
x-direction (→+)
P
F
d(mv x )
= F cos θ − Ff
dt
W
Ff
r
∑F
To write this equation in terms of scalar components, let’s use the x, y coordinate
system shown in Figure 2.7.
Figure 2.7
θ
=
and since m is a constant and vx is the same for every point on the body
N
m
Figure 2.8 - Free body
diagram
dv x
= F cos θ − Ff
dt
y direction (+↑)
d(mv y )
dt
= N − P − W − F sin θ
but since vy is a constant in magnitude and direction we find
N = P − W − F sin θ
Dry Friction model
v x = 0 ⇒ Ff = F cos θ < µ s N
v x ≠ 0 ⇒ Ff = µ k N
Ff
where the coefficients of static friction and kinetic friction are µs and µk
respectively.
µ sN
Let’s consider how Ff varies as a function of the applied force F for θ = 0 and P = 0
and when F increases linearly. The resulting friction force is shown in Figure 2.9.
From this figure, it is clear that as long as F is less than µsN the friction force is just
equal to F (and the object won’t move). As soon as the friction force exceeds µsN
then the object starts to move and therefore the friction force will be equal to µkN.
In general, there are three possible cases involving dry friction as summarized in
Table 2.4.
µkN
µ sN
F
Figure 2.9 - Friction force
as a function of the
applied force F
2–27
Table 2.4 – Dry Friction Cases
Case
1
Description
The object does not slide
2
Motion is impending, but
it is not moving yet.
The object is sliding
3
Magnitude of Friction Force
Unknown (but it must be less than µsN). The
friction force is just an unknown to be solved
for similar to a normal force.
Ff = µsN
Ff = µkN
Note: In problems where it is not clear if the object moves or not, it is usually
necessary to solve for the friction forces assuming there is no motion and then
compare to µsN.
Self test on friction
The coefficient of static friction between the block shown below and the floor is 0.4 and the coefficient of kinetic friction is 0.3. What is
the magnitude of the friction force if
a) P = 15 lb
b) P = 35 lb
P
100 lb
c) P = 50 lb
a) 15 lbf
b) 35 lbf
c) 30 lbf
Example 2/8
Blocks A and B are initially at rest when force P is applied.
A weighs 50 lbf and B weighs 100 lbf and the coefficients of
friction between A and B and between B and the ground are
shown in the figure. Determine the accelerations of blocks A and B.
µs = 0.4
µk = 0.3
µ=0
P
A
B
Strategy: Since we are interested in acceleration, we need to use the rate form of conservation of linear momentum. The first question
we need to ask ourselves in a problem like this is, “Does block A slide on block B?” If it does, then the friction force is µkN, if it
doesn’t, then blocks A and B move together and the friction force will be unknown. How do we determine if it slides? The procedure is
always the same, assume it doesn’t slide and then check your assumption. We have at least two ways we can do this. The first way is to
assume it doesn’t slide and solve for the force P required for sliding to be impending and then compare this P to the actual applied force.
The second way is to assume it doesn’t slide and solve for the friction force, F. If F is larger than µsN, then the assumption is wrong and
the block actually slides. Let’s use the second way.
Assuming no sliding:
Let’s start off by using block A as our system. A free body diagram of A is shown.
LM x-direction (+ →)
dPx
=
dt
∑F
x
P
→ m A a A = P − FA
(1)
FA
LM y-direction (+↑)
dPy
dt
=
mAg
∑F
y
→ 0 = N A − m A g
(2)
NA
2–28
So we have 2 equations and 3 unknowns (aA, FA, NA). To get more equations let’s look at block B as a system.
NA
LM x-direction (+ →)
dPx
=
dt
∑F
x
FA
→ m B a B = FA
(3)
→ 0 = N B − N A − m B g
(4)
mBg
LM y-direction (+↑)
dPy
dt
=
∑F
y
NB
We now have 4 equations and 5 unknowns (aA, FA, NA, NB, aB). We still need one more equation. We originally assumed that block A
does not slide on block B, therefore our last equation is
aA = aB
(5)
We can now solve these equations and compare our friction force to the maximum allowable friction force, which is Fmax = µsN. Note in
the Maple solution shown below that the first thing I did was to calculate the mass of each object in slugs, (recall a slug is a lbf-s2/ft), by
dividing the weight by g.
> WA:=50:
WB:=100:
g:=32.2:
P:=50:
mA:=WA/g;
mB:=WB/g;
mA := 1.552795031
mB := 3.105590062
> eq1:=mA*aA=P-FA;
eq2:=0=NA-mA*g;
eq3:=mB*aB=FA;
eq4:=0=NB-NA-mB*g;
eq5:=aA=aB;
eq1 := 1.552795031aA = 50 − FA
eq2 := 0 = NA − 50.00000000
eq3 := 3.105590062aB = FA
eq4 := 0 = NB − NA − 100.0000000
eq5 := aA = aB
> solve({eq1,eq2,eq3,eq4,eq5});
{ NA = 50., NB = 150., aB = 10.73333333, FA = 33.33333333, aA = 10.73333333}
Therefore the maximum allowable friction force is
Fmax = µsN = (0.4)(50) = 20 lbf
Since FA is larger than this, the assumption that the blocks do not slip is wrong. Therefore we need to resolve the problem. We can still
use Eqs. 1-4, but instead of Eq. 5 we will have
FA = µkN = 0.3NA
Once again we can solve Eqns. 1-4 and 5b for (aA, FA, NA, NB, aB) resulting in (I’ll leave off the Maple codes since it is basically
identical to that shown above except with a different eq5):
{ aA = 22.54000000, aB = 4.830000000, NA = 50., NB = 150., FA = 15. }
So our final accelerations are aA = 22.54 ft/s2 and aB = 4.82 ft/s2.
(5b)
2–29
2.4 Conservation of Linear Momentum (Finite Time)
As shown earlier, the conservation of linear momentum equation for a closed
system can be written as
r
dPsys
dt
Impulse is the area under the
curve
=
r
d (m sys v G )
dt
t2
∫
Favg
t1
r
dPsys
dt
t2
dt =
ext
(2.16)
r
∑∫F
ext dt
t1
r
r
r
∆Psys = Psys2 − Psys1
t
r
∑F
If the forces on the right hand side of equation are functions of time it is a straight
forward matter to integrate Eq 2.16 with respect to time
F(t)
Figure 2.10 – Illustration
of Impulse
=
t2
∑∫
(2.17)
r
Fext dt
t1
where
t2
∫
r
Fext dt = “Impulse” = Fext,avg ∆t
(2.18)
t1
The impulse is just the area under the curve as shown in Figure 2.10
Clues as to when to use the finite
time form of linear momentum
Key idea: When
impulsive forces act on a
system, non-impulsive
forces can be neglected.
The finite time form of linear momentum (LM finite) is usually used when you:
1. have a problem involving impacts,
2. have two specific times,
3. have several interacting bodies and you do not know (or care about) the
internal forces,
4. are given a force as a function of time,
5. want to find times, forces (especially impulsive forces), or velocities.
The reason the finite time form is useful for impact is because if there are impulsive
forces in a problem (an impulsive force is a large force that acts over a small time
to produce a definite change in momentum) then non-impulsive forces, such as
gravitational forces or spring forces, can be neglected. Also, if you pick you
system to be both objects, then the internal impulsive forces will not enter the
equations.
2.4.1 Procedure for applying the conservation of linear
momentum (finite time form) to particles
Just like LM rate form, the finite time form of LM is a vector equation so we will
emphasize drawing pictures, in this case called impulse momentum diagrams. A
complete procedure is shown below.
Procedure
1. Identify the system. For impact problems you often start by picking both
objects as your system.
2–30
2.
Draw impulse-momentum diagrams.
mvG 2
System momentum after the
time interval
3.
4.
mv G1
∫ F dt
=
1
∫ F dt
2
Impulses acting during the time
interval
System momentum before the
time interval
Define a coordinate system to be used when applying conservation of linear
momentum.
Apply the scalar equations for conservation of linear momentum to the
impulse-momentum diagrams. We therefore have two scalar equations
a. Linear momentum in the x-direction
b. Linear momentum in the y-direction
t
2
r
r
∆Psys = Fdt
∫
t1
or if there are impulsive loads acting on the system
r
∆Psys =
r
∑ F ∆t
i
It is important to note that these are vector equations, so just like the rate form, we
can obtain scalar equations by looking at the linear momentum in the x and y
directions and the angular momentum about some point.
5.
Solve the equations for the required unknowns. If the two scalar equations
have more than two unknowns then a kinematic analysis may be required for
the problem solution. If you have an impact you may need to use the
coefficient of restitution equation (Section 3.4). If you still need more
equations try looking at an interrelated system.
Notes:
• If there are impulsive forces acting in the system you can neglect nonimpulsive forces.
• This principle is useful for central force problems.
2–31
Example 2/9
The overhead conveyor drops the 12 kg package A into the 1.6 kg carton B.
The package is “tacky” and sticks to the bottom of the carton.
a) Immediately following the drop, what is the velocity of the combined
package and carton?
b) What is the average impulse exerted on the package?
c) If the coefficient of friction between the carton and the horizontal
conveyor is µk = 0.2, how long will the box slide on the belt?
d) After the block stops sliding on the belt what is the friction force between
the belt and the box?
30°
1 m/s
A
0.2 m/s
B
Strategy: Since the package will experience an impulsive force when it hits the carton, we want to use the finite time form of
conservation of linear momentum. Since we have impulsive forces, we can neglect non-impulsive forces. Also, since we are not given
how far the package A drops before it lands in the box, we will assume it is small, so that the velocity of A will be 1 m/s.
For impact problems, I usually start off by picking both objects as my system so the internal forces don’t enter the problem. We still
may need to isolate one of the objects individually, but this is usually a good way to start.
Impulse-momentum diagrams:
mAvA
30°
(m A + m B )v ′AB
mBvB
R∆t
Momentum
after
Momentum
before
Impulses during
time interval
LM x-direction (+ → )
∆Psys x =
∑ F ∆t
x
→
( m A + m B ) v ′AB − ( m A v A cos 30° + m B v B ) = 0
(1)
We only have one unknown in this equation, so we can immediately solve for v ′AB
v ′AB =
(m A v A cos 30° + m B v B ) (12 kg)(1 m/s) cos 30° + (1.6 kg)(0.2 m/s)
=
(m A + m B )
(12 + 1.6)kg
= 0.788 m/s
So the answer to part a) is 0.79 m/s to the right. Note that in this part of the problem we did not need to use LM finite in the y-direction.
We certainly could have looked at the y-direction, but we would introduce one additional unknown, the impulse in the y-direction, R∆t.
For part b) we are interested in the impulse acting on the package. Therefore, we need to isolate the package as our system. We don’t
really need to bother redrawing the impulse-momentum diagrams since we have basically already done this above, but for completeness
2–32
I will anyway. The only thing that will change is we will now have to worry about the impulsive forces between A and B. If we choose
our system to be block A our impulse-momentum diagrams will be:
mAvA
30°
m A v AB
Fx∆t
Momentum
after
Momentum
before
Fy∆t
Impulses during
time interval
Applying linear momentum in the x and y directions we get
LM x-direction (+ → )
∆Psys x =
∑ F ∆t
x
→
m A v ′AB − m A v A cos 30° = − Fx ∆t
(2)
LM y-direction (+ ↑ )
∆Psys x =
∑ F ∆t
x
→ 0 − (− m A v A sin 30°) = Fy ∆t
(3)
We can immediately solve Eq. 2 and 3 for Fx∆t and Fy∆t giving
Fx∆t = 0.94 kg-m/s to the left
Fy∆t = 0.39 kg-m/s up
For part c) we want to determine how long it will be before the box stops sliding on the belt. The impact is already over and the box and
package are traveling at the same rate, so what do we do? We need another principle! Let’s apply LM rate to find the acceleration and
then we can integrate this to determine how long it is until the velocity of the box and package is equal to the velocity of the belt. To
apply LM rate lets pick the box and package as our system and draw a FBD.
(m A + m B )g
LM y-direction (+↑)
r
dPy
dt
=
∑F
y
→
0 = N − ( m A + m B )g
→ N = (m A + m B )g
(4)
LM x-direction (+ →)
r
dPx
=
dt
∑F
x
→
(m A + m B )a = −µ k N = −µ k (m A + m B )g
(5)
µkN
N
From Eq. 5 we see that the acceleration is
a = -µkg
Since we now have the acceleration, we can find the velocity either one of two ways. We can use our kinematic relationship between
acceleration, velocity and time and separate variables and integrate – always fun, but really not necessary in this case – or we can use the
equations we have already derived for constant acceleration. We will use the constant acceleration equations. We know
v = vo + at
or for our problem
v = vo - µkgt
2–33
The time for the package and box to reach 0.2 m/s is therefore
v o − v 0.788 m/s - 0.2 m/s
=
µkg
(0.2)(9.81 m/s 2 )
= 0.30 s
t=
For part d) we want to know the friction force after the block stops sliding. After the box stops sliding, it will be moving at a constant
velocity and therefore the acceleration will be zero and the force in the x-direction will also be zero. The answer to d) is
Friction force = 0
Example 2/10
A 100-kg object is sitting on a frictionless surface when a force P is applied in the horizontal direction. P varies according to the
accompanying graph, remains constant in direction, and is the only applied external force acting on the body in its plane of motion.
a) What is the velocity of the object after 2 seconds?
P, kN
b) How does your answer change if the surface is not
frictionless? Let µs = 0.35, µk = 0.30.
c) What is the maximum velocity of the block for part b)?
0.4
P
0.2
0
0.5
1.5
1.0
time, s
2.0
Strategy: We have two choices as far as what principle to use when solving this problem. We can use LM rate to find the acceleration
and then integrate to find the velocity. Alternatively, since we are asked for velocity and given a force that is a function of time, we can
use LM finite. We will use this second approach. The block will be our system.
t
∫ mgdt
Since LM finite is a vector equation, let’s start with impulse-momentum diagrams.
0
0
mv2
t
∫ Pdt
0
mv1
t
t
∫ Fdt
∫ Ndt
0
0
(parts b and c)
Momentum
after
Momentum
before
Impulses during
time interval
Let’s look at the x and y direction.
LM y-direction (+ ↑ )
∆Psys y =
∑ F ∆t
y
→
∫
t
∫
t
0 - 0 = Ndt − mgdt
→
0
0
N = mg
(1)
2–34
LM x-direction (+ → )
(part a)
∆Psysx =
∑ F ∆t
x
∫
t
→ mv 2 − 0 = Pdt
(2)
0
We can certainly write P as a function of time and do the integral, but it is a lot easier to recognize that the integral is simply the area
under the curve. Therefore, to find the velocity at t=2 all we need to do is determine the area under the curve.
1
t
∫ Pdt = (400 N)(0.5 s) + 2 (400 N + 200 N)(0.5 s) = 350 N − s
0
so
t
∫ Pdt = 350 N - s
=
0
v2
m
100 kg
= 3.5 m/s
Answer to part a)
For part b) the solution will be exactly the same except we will have friction. The first question to ask is “Will the block even move?” If
it doesn’t move, the friction force will be equal to P, that is, it will have a value of 400 N for 1 < t < 2 s. The maximum allowable
friction force is µsN=(0.35)(100kg)(9.81 m/s2) = 343.35 N. Since the applied force is larger than the maximum allowable, the block
must slide. Let’s apply LM finite again. The y-direction doesn’t change, so let’s just look at the x-direction. There will only be friction
when P is acting, so we will start the integrals at t = 1 s.
LM x-direction (+ → )
(part b)
∆Psysx =
∑ F ∆t
∫
t
∫
t
→ mv 2 − 0 = Pdt − µ k Ndt
x
1
1
Solving for v2 we get for t < 2s
v2 =
t
1 t
Pdt − µ k Ndt
1
m 1
∫
∫
(3)
The velocity at t = 2 s is
2
1 2
Pdt − µ k Ndt
1
1
m
1
=
350 Ns − (0.3)(100 kg)(9.81 m/s 2 )(1 s)
100 kg
Answer to part b)
= 0.557 m/s
v2 =
∫
∫
(
)
This is less than the answer we found in part a), which makes sense. Now, onto part c), that is, what is the maximum velocity? A
natural temptation is to assume that the maximum velocity will occur when at t = 2 s since the applied force is being applied until this
point, but I’m afraid this would be wrong. If you didn’t think this, good for you. How do we find the maximum velocity? We have an
equation for the velocity, so all we need to do is take the derivative of Eq. 3 and set it equal to zero to find when the velocity will be a
maximum.
dv 2
1
= 0 = (P − µ k N )
dt
m
→ P = µ k N
From Eq. 4, the maximum will occur when the applied force is equal to the
friction force. Does this make sense? Yes! The derivative of the velocity is
just the acceleration, so the acceleration will be zero when P= µkN, which we
could have also found using LM rate. When does the applied force equal µkN?
µkN = 0.3 (100 kg)(9.81 m/s2) = 294.3 N. We can find the time, let’s call it t*,
at which this occurs simply by looking at our figure of P vs time as shown.
(4)
P, N
400
294.3
200
0
0.5
1.5 2.0
1.0
*
time, s t
2–35
Using similar triangles
t * − 1.5
2.0 − 1.5
=
→ t * = 1.764 s
400 − 294.3 400 − 200
We can now find the velocity using Eq. 3.
v2 =
1 1.764 1.764
Pdt − µ k Ndt
1
m 1
∫
∫
1
1
2
[(400 N)(0.5 s) + (400 N + 294.3N)(1.764 − 1.5) s)] − (0.3)(100 kg)(9.81 m/s )(1.764 − 1) s)
100 kg
2
Answer
to
part
c)
= 0.669 m/s
=
Let’s look at some “what if” scenarios. What if I had asked you how long it will take the block to stop? We know it has a velocity at t =
2 s, so all we need to do is use Eq. 3 and set v2 = 0 as shown below
v2 =
t
1 2
Pdt − µ k Ndt = 0
1
m 1
∫
∫
so
t
∫µ
1
k Ndt
∫
2
= Pdt
1
µ k N( t − 1) = 350
→ t = 1 +
350
350
= 1+
= 2.19 s
µk N
0.3(100)(9.81)
The block will stop at t = 2.19 s. How could we make this problem more interesting? What if we
applied the force P at an angle of 20° as shown? What changes? The main difference is that the
normal force will depend on P and will therefore also be a function of time. Before, it was always a
constant. We can still use Eq. 3, we just need to be careful to remember that the normal force
depends on time when we do the integral.
P
2.4 Conservation of Angular Momentum
In this section I want to introduce the concept of angular momentum. We will not
use it very much in the treatment of particles, but it will be very important in the
treatment of rigid body rotation so I want you to get familiar with it now.
Path of particle
y
What is angular momentum?
r
r
P
r
v
x
z
Figure 2.1 - A particle
traveling through space
r
You will recall that linear momentum of a particle of mass m and velocity v , is
defined to be
r
r
P = mv
(2.4)
Remember that linear momentum is a vector, that is, it has a magnitude and a
direction.
Angular momentum is simply the “moment of momentum”.
Mathematically, the angular momentum of a particle about any point O is
r
r
L O = rP / O × mv
(2.19)
2–36
There are a number of important things to note about angular momentum:
1. Angular momentum is always with reference to some point. To say “The
angular momentum of the particle is …” makes no sense. You should say,
“The angular momentum of the particle about point ___ is ….”.
2. Angular momentum is a vector quantity, that is, it has a magnitude and a
direction. This is clear from the cross product. The direction of the angular
r
r
momentum will be perpendicular to rP / O and v and its sense can be
3.
determined using the right hand rule.
For a 3D problem it is usually easier to use the cross product, but when it is a
2D problem, we will often just use the project of mv and the perpendicular
distance from the line of action.
It has been my observation that many students have difficulties taking moments.
Since angular momentum is simply a moment, let’s do a quick review of what a
moment due to a force is.
Review of a “moment” of a force (also called a torque):
L
A
F
θ
What is the moment about A due to F? From physics or statics you should know
r
r r
that the moment is M A = r × F . We could take the cross product, but it is a lot
easier to take the force times its perpendicular line of action. We have two ways of
doing that in this problem as shown below.
Method 1: Find the distance from the line of action of F to point A.
L
A
F
Perpendicular
distance
θ
Line of action
From this figure it is clear that the perpendicular distance is Lcosθ, so the moment
r
is M A = FL cos θ (counterclockwise).
Method 2: We can resolve F into x and y components and multiply these
components by their perpendicular distances.
2–37
L
A
F sinθ
F θ F cosθ
Perpendicular
distance
Line of action
It is clear from this figure that F sinθ passes through point A, so its contribution to
the moment will be zero, and F cosθ will have a moment arm equal to L.
r
Therefore, we get the same answer we got before, that is, M A = FL cos θ
(counterclockwise). So, you are now an expert in taking moments of forces in 2D.
You determine angular momentum in exactly the same way, but instead of it being
a moment due to a force, it is a moment due to momentum.
Check yourself: Angular momentum
At the instant shown, determine the angular momentum of the object shown below about points
a) A,
b) B
A
c) C
mv
L1
L2
G
answer
B
L3
C
Check yourself again
Particle P has a mass, m, and a speed, v, as shown. What is the angular momentum of the particle about point O?
P
r
O
answer
mvrsinθ (counterclockwise)
v
θ
It is important to note that I can take angular momentum about any point I want to.
The point does not have to be on the object. The object does not need to be
rotating about the point. All I need to know is where the point is with respect to the
center of gravity of the object and the velocity of the center of gravity.
2–38
How do you calculate the angular momentum of a system of
particles?
For a system of particles, the angular momentum about any point can be
determined by adding up the angular momentum for each mass,
# of
particles
r
r
r
L sysO =
ri / O × m i v i
∑
(2.20)
i =1
For a continuous system this summation can be changed to an integral over the
volume of the system
r
r r
r r
L sysO = r × vdm = r × vρd∀
(2.21)
∫
y
G
rG
z
x
∫
∀
m sys
where ρ is the density and ∀ is the volume. The evaluation of the integral can be
very difficult, so in this chapter we will limit ourselves to the very simple case of
translation. In the next chapter we will look at problems involving rotation. In the
case of translation, every point of the continuous system will have the same
velocity. Therefore, we can pull the velocity out of the integral as shown below
Figure 2.2 - Center of mass
r
L sysO =
r
r
∫ rdm × v
m sys
But from Eq. 2.9 we know that
r
r
∫ rdm = r
G m sys
m sys
We also know that the velocity of every point on a translating body is the same, so
r r
v = v G and Eq. 2.21 becomes
r
r
r
L sysO = r × m sys v G
Angular momentum
of a translating body
(2.22)
In Chapter 4 we will discuss how to calculate the angular momentum for rotating
bodies. We now know how to calculate the angular momentum of a particle and a
translating body, so all we need to know is how angular momentum can enter or
leave a system.
How can angular momentum be transported into or out of a
system?
There are primarily two mechanisms by which angular momentum can be
transported: by moments and with mass. When an external force, F, is applied to a
system, it may produce a moment with respect to any point O depending on the line
of action of F. If F does produce a moment, this moment represents a transport rate
of angular momentum. Any pure moment or couple will also represent a transport
of angular momentum. More specifically, the net transport rate of angular
momentum about point O into a system due to external forces is written
mathematically as the sum of the individual moments:
r
∑M
O
= rate of transport of angular momentum at non-flow boundaries.
2–39
Similar to the case of linear momentum, angular momentum can also be transported
into or out of the system with mass. Each little lump of mass that enters or leaves a
system with a velocity, v, will potentially have angular momentum about some
point, O. Thus, the angular momentum of an open system can also be changed by
mass flow carrying angular momentum across the system boundary. The rate at
which angular momentum about point O is transported across the boundary is equal
to the mass flow rate multiplied by the local velocity at the boundary assuming that
the velocity is uniform. That is:
r
r
& v = rate of transport of angular momentum due to mass flow
r×m
The net transport of angular momentum with mass can be determined by summing
the transports over all the inlets and outlets of the system:
Net transport rate of angular momentum
=
into the system with mass flow
r
r
∑ r × m& v − ∑ r
i
i
r
i
in
o
r
& ovo
×m
out
How can angular momentum be generated or destroyed?
It can’t! Angular momentum is conserved. The basis for this conclusion is years
of empirical evidence.
Finally, the rate form for conservation of angular momentum can be written as
Rate of Accumulati on
of Angular Momentum
inside system at time t
Net rate of transport
= of Angular Momentum
into the system by
external forces at time t
Net rate of transport
of Angular Momentum
+
into the system by
mass flow at time t
or in terms of symbols, conservation of angular momentum (rate form ) becomes
Important Equation!
Conservation of
Angular Momentum
(rate form)
r
dLsys0
dt
=
r
∑ M +∑ r × m& v −∑ r × m& v
r
o
in
r
r
i i
r
o o
(2.23)
out
where
r
r
r
L sysO = r × mv G = angular momentum of a particle or translating rigid body about
point O.
m = mass of the system
r
v G = velocity of the center of gravity
r
M o = external moment about point O
& i = mass flow entering the system
m
r
v i = velocity of mass entering the system
& o = mass flow exiting the system
m
r
vo = velocity of mass exiting the system
2–40
Common situations
1. Steady state. In this class steady state means that all intensive properties and
interactions are independent of time. Applying this to conservation of linear
momentum we get
r
0
dLsys0
=
dt
0=
r
∑ M +∑ r × m& v −∑ r × m& v
r
o
∑
r
Mo +
in
∑
in
r
r
i i
r
r
& i vi −
r ×m
out
r
o o
∑ r × m& v
r
r
o o
out
2. Closed system. A closed system means we have no flow at the boundaries, so
conservation of angular momentum becomes:
Important Equation!
Conservation of
Angular Momentum
(rate form) for a
closed system – this
is what we will use
most often in this
book
r
dL sys0
dt
r
dL sys0
dt
=
=
∑
r
Mo +
∑
r
Mo
∑
in
0
r
r
& i vi −
r×m
∑
0
r
r
& o vo
r ×m
out
(2.24)
Modeling Reactions at Supports and Connections
A key to modeling a system correctly is identifying the forces and moments acting
on the system due to supports and connections. These forces and moments are
usually referred to as reactions. In Beer and Johnston’s dynamics book (F. P. Beer
and E. R. Johnston Jr, Vector Mechanics for Engineers: Statics, 6th ed., McGrawHill, New York, 1996) reactions are classified in three broad categories:
(a) Force with a known line of action. Many connections satisfy this condition
such as rollers, rockers, frictionless surfaces, short links and cables, collars on
frictionless rods, and frictionless pins in slots. Each of these reactions is
characterized by the ability to only transport linear momentum by a force in a
single, clearly identifiable direction.
(b) Force of unknown direction and magnitude. Hardware or connections that
provide this type of reaction include frictionless pin, frictionless ball-and-socket
joints, hinges, and rough surfaces. (Although frictionless surfaces only transmit a
force normal to the surface, friction introduces shear forces at the surface.)
(c) Force of unknown direction and magnitude and a couple. This last type of
reaction is usually referred to as a fixed support. The reaction of the ground on a
telephone pole stuck vertically in the ground is an excellent example. When you
push on the telephone pole in any direction, the ground exerts three forces on the
pole—a horizontal shear force, a vertical normal force, and a distributed force that
is a force couple. The couple, as shown earlier, only transmits angular momentum.
Figure 2.11 has some of the most common support conditions we will encounter in
this book. Although these are idealized conditions, they do a pretty good job of
modeling support conditions. Believe it or not, rollers were actually used in the
design of some bridges at the connection between spans. An example of an actual
“roller” condition on an old bridge is shown in Figure 2.12.
2–41
Figure 2.12 – A “roller” connection
between adjacent spans of an old
bridge. Bridges no longer have
connections of like this.
Figure 2.11 – Forces acting at supports (from Basic Engineering Science –
A Systems, Accounting, and Modeling Approach by D.E. Richards)
Example 2/11
Water flows out of a fire hydrant at 5 ft3/s at both A and B, both
of which have cross sectional areas of 0.04 ft2 as shown below. The
pressure at the inlet is 120 psig and the inlet cross-sectional area
is 0.75 ft2. Neglecting the weight of the hydrant and the water in the
hydrant, determine the reactions (forces and moment) at the base of the
hydrant. The mass flow rates at A and B have been calculated for you
using a density of water equal to 1.938 slug/ft3 or about 62.4 lbf/ft3.
20”
& = 5 ft 3 / s
∀
A
& A = 9.69 slug/s
m
& = 5 ft 3 / s
∀
B
& B = 9.69 slug/s
m
Area = 0.04 ft 3
Area = 0.04 ft 3
A
B
30”
30°
24”
C
Pi = 120 psig
Area =Ai= 0.75 ft2
Strategy: Since we are interested in forces and moments we will want to use the rate forms of linear and angular momentum. As a
system we will pick the hydrant. Since the system is not moving our principles will be:
Linear momentum: 0 =
r
∑ F +∑ m& v −∑ m&
i
r
i
in
Angular momentum: 0 =
r
o vo
out
r
∑ M +∑ r × m& v −∑ r × m& v
r
o
in
r
r
i i
out
r
o o
2–42
Let’s start by drawing a FBD for our external forces and moments and a mass flow diagram (MFD) for our mass flow rates. Since the
base is fixed, we will replace the ground with two forces, Rx and Ry, and a moment, M. We also need to put in the force due to the inlet
pressure, which will just be the pressure multiplied by the inlet area.
20”
FBD
MFD
A
& AvA
m
B
20”
& BvB
m
A
B
30”
30”
24”
Ry
C
30°
24”
C
M
Rx
PiAi
& i vi
m
Applying conservation of linear and angular momentum we get:
LM x-direction (+ →)
0=
∑ F +∑ m& v −∑ m& v
x
i ix
& B v B cos 30° − m
& A vA )
→ 0 = R x + 0 − (m
o ox
in
out
(1)
LM y-direction (+↑)
0=
∑ F +∑ m& v −∑ m& v
y
i iy
o oy
in
& i vi ) − (m
& B v B sin 30°)
→ 0 = R y + Pi A i + (m
(2)
out
AM about center point of inlet (+ Counterclockwise (CCW))
0=
r
∑ M +∑ r × m& v −∑ r × m& v
r
o
r
r
i i
in
r
o o
out
30
20
24
& A vA (
& B v B sin 30°( ft ) − m
& B v B cos 30°( ft )
ft) + m
→ 0 = M + 0 - m
12
12
12
(3)
& A,m
& B , Pi , A i so we have 7 unknowns ( m
& i , v i , v B , v B , R x , R y , and M ). We only have 3 equations, so we
In Eqs. 1-3 we know m
need to get the mass flow rate at the inlet and the velocities using something other than linear and angular momentum. Where do we get
more equations? Easy, we see a mass flow rate, so we naturally think of conservation of mass and we can determine the inlet and outlet
velocities using the definition of mass flow rate given in Eq. 2.13. Using the hydrant as our system, conservation of mass is
dm sys
dt
=
∑ m& − ∑ m&
i
o
&i −m
&A −m
&B
→ 0 = m
(4)
Using the definition of mass flow rate we get:
& A = ρv A A A
m
(5)
& B = ρv B A B
m
(6)
& i = ρv i A i
m
(7)
2–43
We now have 7 equations and 7 unknowns which we can solve by hand or using Maple. The only thing we have to be careful about is
to convert the inlet pressure to lbf/ft2 so when we multiply it by the area we get lbf. The Maple solution is shown below.
> A:=0.04:
Ai:=0.75:
rho:=1.938:
mdotA:=9.69:
mdotB:=9.69:
Pinlet:=120*144:
> eq1:=0=Rx+0-(mdotB*vB*cos(30*Pi/180)-mdotA*vA);
eq2:=0=Ry+Pinlet*Ai+mdoti*vi-mdotB*vB*sin(30*Pi/180);
eq3:=0=M+0-(mdotA*vA*30/12+mdotB*vB*sin(30*Pi/180)*20/12mdotB*vB*cos(30*Pi/180)*24/12);
eq4:=0=mdoti-mdotA-mdotB;
eq5:=mdotA=rho*vA*A;
eq6:=mdotB=rho*vB*A;
eq7:=mdoti=rho*vi*Ai;
eq1 := 0 = Rx − 4.845000000vB 3 + 9.69 vA
eq2 := 0 = Ry + 12960.00 + mdoti vi − 4.845000000vB
eq3 := 0 = M − 24.22500000vA − 8.075000000vB + 9.690000000vB 3
eq4 := 0 = mdoti − 19.38
eq5 := 9.69 = 0.07752vA
eq6 := 9.69 = 0.07752vB
eq7 := mdoti = 1.45350vi
> solve({eq1,eq2,eq3,eq4,eq5,eq6,eq7});
{ vA = 125., vB = 125., mdoti = 19.38000000, vi = 13.33333333, M = 1939.553459, Rx = -162.2767297,
Ry = -12612.77500}
So our final answers are
Rx = 162.3 lbf (left), Ry = 12,610 lbf (down) and M = 1939 lbf-ft (CCW)
Example 2/12
A satellite is traveling around the earth in the elliptical
path shown. If the radius of the earth is 6371 km, determine
the velocity of the satellite at point B if the satellite has a
velocity of 33,800 km/hr at position A. Assume the center
of the earth is fixed.
vA
A
B
O
390 km
13520 km
Strategy: What choice of principles do we have at this point? We can use LM rate, LM finite or conservation of angular momentum.
Since the only force acting on the satellite will be gravity, which is always directed towards point O, it turns that out the easiest way to
solve this problem is to use angular momentum about point O.
2–44
No matter where the satellite is in its trajectory, gravity will act towards point O. Therefore, the moment due to gravity about point O
will be zero. Therefore, if we pick the satellite as our system we have
r
dL sys0
dt
=
∑
r
Mo +
∑
r
r
& i vi −
r×m
in
∑
r
r
& ovo
r ×m
→
r
dL sys0
dt
out
=0
or
r
L sysO = 0
So the angular momentum of the satellite about point O must always be constant. We can therefore set the angular momentum at A
equal to the angular momentum at B.
mrA v A = mrB v B
→ v B =
rA v A
rB
where
rA = 6371 km + 390 km = 6761 km
rB = 13,520 km+(13,520 km – 6761 km)=20,279 km
giving
(6,761 km)(33,800 km/hr)
20,279 km
= 11,295 km/hr
vB =
Example 2/13
A completely filled barrel and its contents have a combined
mass of 160 kg. A cylinder C is connected to the barrel at a
height h = 0.6 m as shown in the figure. The coefficient of
static friction is 0.48 and the coefficient of kinetic friction is 0.40.
Determine the maximum value of C so that the block will not
tip over.
0.6 m
0.9 m
h=0.6m
0.45 m
A
B
C
Strategy: Since we have forces involved and we are really just looking at this instant in time we will want to use the rate form of
conservation of linear momentum and angular momentum. This problem is different from others we have looked at so far since the
object could potentially tip over. It is important to note that we are told the barrel doesn’t tip over so it will just be translating. The
problem where the barrel actually tips over and rotates will be looked at in Chapter 4.
Before we can determine the maximum value of C, we need to determine whether or not the barrel will slip. To do this, let’s solve some
statics problems, that is, let’s find out a) the mass of C required so that the barrel is just starting to tip, but not slip, and b) the mass of C
required to cause the barrel to slide.
2–45
T
Mass required if the barrel tips but does not slip:
Let’s start by picking block C as our system. Drawing a FBD we get the figure shown. Using conservation of
LM in the y-direction and recognizing that if the block is not moving, the left hand side will be zero, we get:
LM y-direction (+↑)
dPsys y
dt
=
∑F
y
→ 0 = T − m c g
mcg
(1)
We have two unknowns in this equation, mc and T. If we now pick the barrel as our system, we can draw
another FBD. In this FBD I am assuming the barrel is about to tip, and therefore, the normal force, N, and
the friction force F will both be acting at the lower right corner of the barrel. Applying LM and AM, again
assuming the barrel is not moving we get:
T
mBg
LM x-direction (+ →)
dPsys x
dt
=
∑F
x
B
→ 0 = T − F
(2)
F
N
LM y-direction (+↑)
dPsys y
dt
=
∑F
y
→ 0 = N − m B g
(3)
AM about B (positive CW)
dL sysB
dt
=
∑M
B
→ 0 = T(0.6) − m B g (0.3)
(4)
We now have 4 equations and 4 unknowns (T, F, mc, N) which we can solve in Maple as shown below.
> mB:=160:
g:=9.81:
> eq1:=0=T-mc*g;
eq2:=0=T-F;
eq3:=0=N-mB*g;
eq4:=0=T*(0.6)-mB*g*0.3;
eq1 := 0 = T − 9.81 mc
eq2 := 0 = T − F
eq3 := 0 = N − 1569.60
eq4 := 0 = 0.6 T − 470.880
> solve({eq1,eq2,eq3,eq4});
{ mc = 80., F = 784.8000000, N = 1569.600000, T = 784.8000000}
So, the mass of C if the block tips without slipping is 80 kg. Let’s find the mass of C required to cause the barrel to just start to slide.
Mass required to cause the barrel to slip:
Eqns. 1, 2 and 3 will not change, but Eqn. 4 will because we will not know where the resultant normal force acts. Therefore, we will
only have 3 equations and 4 unknowns. Fortunately, we said the block was about to slide. In this case, the friction force will be equal to
the normal force times the coefficient of static friction as shown in Eq. 4b
F = µs N
We now have 4 equations (1,2,3 and 4b) and 4 unknowns (T, N, F, mc) Solving these we find
mc = 76.8 kg
(4b)
2–46
How do we interpret this? It means that the force required to cause the barrel to slip is 76.8 kg, which is less than the force required to
cause the barrel to tip without sliding. Therefore, it is impossible for the barrel to tip without sliding, so the barrel will be sliding and
tipping at the same time. So, we need to solve the problem again, except this time with C and the barrel accelerating.
Barrel slides and tips:
We will still be using the same principles used above except in this case both the barrel and the mass C will move. Therefore, LM for
block C will be (note that in this case I made positive down since that is the direction C would move):
LMy-direction (+ ↓)
dPsys y
dt
=
∑F
→ m c a c = m c g − T
y
(1c)
We have 3 unknowns in this equation, mc, T and ac. We need at least two more equations. For the barrel, equations 2 and 4 will change.
In this case let’s redraw our FBD and also draw what I call a “kinetic diagram”. We will discuss this in more detail in the next chapter,
but on the kinetic diagram you put all your acceleration terms, in this case just the mass times the acceleration of the barrel. The kinetic
diagram makes applying angular momentum much easier in my opinion. The FBD and KD for the barrel are shown below.
FBD
KD
T
mBg
mBaB
B
B
µkN
N
The normal force is again drawn at B since we are assuming that the barrel is about to tip, and the friction force is the coefficient of
kinetic friction times the normal force since we know the barrel is sliding. Applying conservation of LM in the x-direction (the ydirection won’t change) we get
LM x-direction (+ →)
dPsys x
dt
=
∑F
→ m B a B = T − µ k N
x
(2c)
We now have 3 equations (1c, 2c, 3) and 5 unknowns (T, mc, ac, aB, N). We can use angular momentum about any point we like to get
another equation. Let’s use point B just to show how to use the kinetic diagram. Recall that conservation of angular momentum for a
closed system about any point O is
dL sysO
dt
=
∑M
O
All this means is that the moment of the terms on your kinetic diagram about any point must be equal to the moment of the terms on
your free body diagram. For this problem, when we apply angular momentum about point B we get
AM about B (positive CW)
dL sysB
dt
=
∑M
B
→ m B a B (0.45) = T(0.6) − m B g (0.3)
(4c)
We still need one more equation. We don’t have any more LM or AM equations and we have already looked at both possible systems.
The last equation comes from kinematics. Since the two blocks are connected by a cable, they will have the same acceleration. Than is,
2–47
ac = aB
(5c)
We now have 5 equations (1c,2c,3,4c,5c) and 5 unknowns (T, mc, ac, aB, N) which we can now solve. A Maple solution is shown below.
> mB:=160:
g:=9.81:
muk:=0.4:
> eq1c:=mc*aC=mc*g-T;
eq2c:=mB*aB=T-muk*N;
eq3:=0=N-mB*g;
eq4c:=mB*aB*0.45=T*(0.6)-mB*g*0.3;
eq5c:=aC=aB;
eq1c := mc aC = 9.81 mc − T
eq2c := 160 aB = T − 0.4 N
eq3 := 0 = N − 1569.60
eq4c := 72.00 aB = 0.6 T − 470.880
eq5c := aC = aB
> solve({eq1c,eq2c,eq3,eq4c,eq5c});
{ N = 1569.600000, T = 1255.680000, aB = 3.924000000, aC = 3.924000000, mc = 213.3333333}
So, the smallest mass of C that will cause the barrel to tip is mC = 213.3 kg.
2.5 Conservation of Energy
In this section I will discuss the last conservation principle we will be using in this
book, conservation of energy. I will start by presenting it in the form we will use it,
often called the “work-energy principle”, and then proceed to discuss it in more
detail, in particular, how to apply it to particles. The full blown rate form of
conservation of energy is
dE sys
dt
& +W
& +
=Q
∑ m& h +
i
in
v2
+ gz −
2
i
∑ m&
out
o h +
where
E sys = E k + E G + E s + U + ... (that is, system energy =
v2
+ gz
2
(2.25)
o
kinetic energy +
gravitational energy + elastic energy + internal energy + ...)
& = net rate of heat transfer into the system
Q
& = net power into the system
W
h = specific enthalpy
zi = vertical distance of the inlet from an arbitrary datum
zo = vertical distance of the outlet from an arbitrary datum
We will never use this form of conservation of energy in this book, but I wanted
you to see it in all of its glory because it is just so beautiful. In this class, we will
only apply conservation of energy to closed systems (no mass flow terms),
adiabatic systems (no heat transfer) and we will use the finite time form of the
equation.
The finite time form of conservation of energy for a adiabatic, closed system is
2–48
Key Principle – The
finite time form of
conservation of energy
for an adiabatic closed
system.
∆E sys = W
(2.26)
where:
W = Work of all external forces and moments
2
r r
(Recall for a force: W = F ⋅ d r )
∫
1
Esys = Ek + EG + Es + U ... = total energy in the system
1
mv 2 for each particle in the system
2
(Note: For rigid bodies the kinetic energy will be different).
Ek = kinetic energy =
EG = gravitational potential energy = mgz for each particle in the system
(Note: z is measured from the datum to the center of gravity).
1
Es = elastic potential energy for a linear spring = kx 2 for each spring in
2
the system
(Note: x is measured from the free length of the spring).
U = internal energy in the system
We will usually not need internal energy because the change of internal energy of
the systems we will look at is usually zero. The only exception is when we have an
impact.
Clues as to when to use
conservation of energy
When should we use this principle? The finite time form of conservation of energy
is often the principle to try first when
1) You have a problem involving two locations in space, that is, two times
2) You want to find velocities, displacements or forces (sometimes)
3) You have forces that do work or are given a force as a function of
displacement.
Many problems that you can solve using conservation of energy can also be solved
using conservation of linear and/or angular momentum. Why use energy? Because
it often makes the problems easier. One reason for this is that it is a scalar
equation, that is, we don’t have to worry about directions like we do with vector
equations like linear and angular momentum.
A procedure for applying this principle is shown below:
Procedure for applying
conservation of energy
1.
2.
3.
4.
5.
Identify the system (usually pick everything you can).
Draw diagrams of the system in position 1 and position 2.
Locate a datum (if any center of gravity changes elevation).
Calculate each term in the energy equation.
If you need more equations, try kinematics.
2–49
Before we look at some examples, I want to discuss the work of a force in more
detail and also to show you how you can derive the work-energy equation from
linear-momentum.
The following discussion of mechanical work and the work-energy principle will
follow closely the development in Basic Engineering Science – A Systems,
Accounting and Modeling Approach by D.E. Richards.
Mechanical Work
Fn
r
dr
t
r
F
n
∫
∫
1
θ
Ft
2
r
r
The mechanical work done by a force F is defined to be
2
r r
r r 2
Wmech = F ⋅ d r = δWmech where δWmech ≡ F ⋅ d r
1
(2.27)
1
r
where d r is the differential displacement vector of the point of application of the
force on the boundary and 1 and 2, respectively, refer to the initial and final
positions of the boundary as shown in Figure 2.13. Using the definition of dot
product we see that
r r
δWmech = F d r cos θ
Figure 2.13
=F
(cosθds)
1
424
3
=
(Fcosθ)
1
424
3
ds
(2.28)
Ft = component of the
force in the direction
of the motion
Component of the
displacement that is
parallel to the force
Therefore, we have two ways of interpreting the differential amount of work. We
can interpret it as 1) the product of the force and the component of the displacement
in the direction of the force, or 2) the product of the displacement and the
component of the force in the direction of the displacement. An alternative
expression to Eq. 2.27 is
2
r r 2
(2.29)
Wmech = F ⋅ d r = Ft ds
∫
1
∫
1
Let’s make some observations about work.
1. Mechanical work is a scalar quantity. It can be positive or negative. For
example, if I lift a book from a table, the work of the force applied by my
hand in lifting the book is positive – the force and the motion are in the
same direction. If I then lower the book, the work will be negative – the
force still acts up, but the motion is down.
2. Work has the dimensions of [Force][L] or units of N-m in SI or ft-lbf in
the USCS system. These are both units of energy.
3. The integral, and hence mechanical work, can only be evaluated if one
knows the end states and the path of the process connecting these states.
This means you must know the force as a function of displacement to
evaluate the integral.
4. Mechanical work for a system cannot be evaluated in a specific state or at
a specific time. It can only be evaluated for a process, that is, a change in
state. Mechanical work is an example of a path function because it can
only be determined when the path of the process is known.
Now let’s look at the work of some common forces.
2–50
Check yourself
Determine the work done by F when the block moves from position 1 to position 2 for the cases shown below. Note: The force F is not
necessarily causing the motion, it is just one of many forces that may be acting on the system as it moves.
Position 1
F
a)
Position 2
F
α
α
Position 1
b)
Position 2
d
d
F
F
d)
Position 2
Position 1
F
F
d
d
Position 1
Answers
a) Fdcosα
b) 0
c) Fd
d) -Fd
c)
Position 2
F
F
Example 2/14 Work of a force that depends on displacement.
A nonlinear spring has a force versus deflection relationship given by F = 2x+3x2 where F is in Newtons and x is in meters. If a mass
is placed on the spring and it is found that the spring deflects 0.2 m from its unstretched length, what is the work done by the spring on
the mass?
Strategy: Since we are given a force and we want to find the work, we just need to apply the definition of work. Rarely will we actually
have to take a cross product. In this case, since the spring will be in compressed, the work will be negative, that is, the force and the
direction of the motion are in opposite directions.
From the definition of work we get
2
x
1
x1
0.2 m
2
r r
W = F ⋅ dr = − Fdx
∫
∫
F(x)
Substituting in for F we get
0.2
W =−
∫ (2x + 3x
2
0
2
)dx = x + x
3
F(x)
0.2
0
Position 1
= −0.048 N − m
The most common mistake on this type of problem is for students to forget the negative sign.
Position 2
2–51
Mechanical Power
Power is the rate at which work is done. For a force, F, acting on a system, the
power is defined to be
r r
&
W
mech = F ⋅ v
(2.30)
r
r
where v is the velocity of the point of application of the force F on the boundary
of the system. The relationship between power and work can easily be shown by
integrating the power with respect to time
t2
∫
t1
t2
&
W
mech dt =
t2
t2
r
r r
r r
r ds
F ⋅ v dt = F ⋅ dt = F
⋅ d s = Wmech
{
dt
t
t δW
∫( ) ∫
∫
1
1
t1
or to summarize , and eliminate the intermediate steps,
t2
∫ W&
mech dt
= Wmech
(2.31)
t1
Let’s make some observations:
a) Mechanical power, unlike mechanical work, has a value at an instant in
time. Recall that work is a path function, that is, it depends on the path
and the two end states of the process.
b) The dimensions for mechanical power are [Force][L]/[T] or [M][L]2[T]-3.
c) The units of mechanical power are N-m/s = J/s = W (Watt) in SI and ftlbf/s or hp in USCS.
Conservation of Energy from Conservation of Linear
Momentum
Now I want to show you how you can derive the conservation of energy equation,
at least the way we will use it, Eq. 2.26, from conservation of linear momentum.
The main reason for showing you this derivation is so that you understand that it is
possible to put terms on either side of the equation depending on how you define
your system. For example, if you use gravitational potential energy, then you
don’t need to calculate the work done by gravity. If you put a linear spring in the
system and use elastic potential energy, you don’t need to find the work due to the
spring force. If the spring is outside the system, then you do need to find the work.
Let me show you what I am talking about.
Warning: Derivation of Conservation of Energy from Conservation of Linear
Momentum.
Starting with conservation of linear momentum for a closed system we have
r
r
dPsys
=
F
(D1)
dt
Let’s break the sum of the forces into two parts and for simplicity we will consider
a single particle
∑
∑
r
F=
r
R
{
net external
contact force
+
r
m
{g
weight of
the system
(D2)
2–52
and
r
dPsys
=m
r
dv
dt
(D3)
dt
Substituting Eq. D2 and D3 into D1 we get
r
r
dv r
m
= R + mg
dt
Let’s move the weight to the other side of the equation and take the dot of the
r
resulting expression with v
r
r r r r
dv
− mg ⋅ v = R ⋅ v
m
dt
r
(D4)
r r
r
dv
&
m ⋅ v − mg ⋅ v = W
mech
1
2
3
dt4
1
42
3
inertia term
gravitational
term
Now, let’s look at the inertia term and the gravitational term in more detail.
r
inertia
dv r m d r r
(v ⋅ v )
m
=
⋅v =
term
dt
2 dt
( )
m d 2
d 1
dE k
v = mv 2 =
=
dt
2 dt
dt 2
(D5)
where
1
mv 2 = kinetic energy of a particle
2
When looking at the gravitational term, we will assume that gravity acts in the
negative z-direction.
r r
gravitational
= mg ⋅ v = − mgkˆ ⋅ ( v x ˆi + v y ˆj + v z kˆ )
term
Ek =
= −mg v x {
kˆ ⋅ ˆi + v y {
kˆ ⋅ ˆj + v{z {
kˆ ⋅ kˆ
=0
=0
dz =1
dt
dE
d (mgz)
dz
= −mg
=−
=− G
dt
dt
dt
( )
( ) ( )
(D6)
where
E G = mgz = gravitational potential energy of a particle
Substituting D5 and D6 into D4 we get
r
r r
dv r
&
m ⋅ v − mg ⋅ v = W
mech
1
2
3
dt4
1
42
3
inertia term
gravitational
term
dE k dE G &
−−
= Wmech
dt dt
d(E k + E G ) &
= Wmech
dt
This is the rate form of conservation of energy. If we integrate this by multiplying
through by dt, we get the finite time form
2–53
t2
∫
t1
d(E k + E G )
dt =
dt
t2
t2
t2
t2
∫ dE + ∫ dE
k
t1
t1
G
=
∫ W&
mech dt
t1
∫ W&
mech dt
t1
∆E k + ∆E G = Wmech
14243
∆E sys
so
∆E sys = Wmech
where the right hand side is the work due to all external forces.
k
F
F
x2
x1
Figure 2.14 – An ideal spring
Force
End of Derivation
Elastic Potential Energy
The only thing we are missing in the derivation shown above is elastic potential
energy, which we will define to be the energy stored in an ideal linear spring,
Figure 2.14. An ideal spring is defined to be massless with no energy dissipation
and an ideal linear spring has a linear force versus displacement relationship as
shown in Figure 2.15 and given by
F = k (x 1 − x 2 ) = kx rel
k
1
Relative Displacement
Figure 2.15 – Force-displacement
relationship for an ideal linear
spring
where xrel is the amount the spring is stretched or compressed from its unstretched
length, also called its free length. We will usually drop the “rel” subscript for
convenience. The energy stored in a linear spring is
1
E s = kx 2
(2.32)
2
where x is measured from the free length of the spring. Let’s look at an example,
so we can see where this comes from.
Example 2/15 Spring in the system or out?
A block slides on a frictionless plane and is attached to an ideal linear spring as shown. When the spring is compressed a distance x1
(measured from the free length of the spring) the velocity of the block is v1. Determine the velocity of the block after the spring is
deflected a distance x2 from the free length of the spring using:
a) A system that is just the block,
k
b) A system that includes the spring.
m
Strategy: Since we are given two positions, x1 and x2, and we want to determine a velocity, v2, let’s use conservation of energy.
For part a) we are told to use a system that is just the block. First, draw a FBD of our system (yes, even when
we use conservation of energy, it is helpful to draw a free body diagram so we can determine what forces will
do work.) Our FBD at some intermediate position, x, is shown.
mg
kx
Applying conservation of energy we get
E sys2 − E sys1 = W
(1)
N
2–54
Since the block does not change elevations, we will only have kinetic energy at position 1 and 2:
E sys1 = E k1 =
1
mv12
2
(2)
E sys2 = E k 2 =
1
mv 22
2
(3)
The only external contact force on the boundary of our system that does work is the spring force. The normal force does no work since
it is always perpendicular to the motion. The work of the spring force is found by using the definition of work and integrating:
x2
1
1
Wspring = − kxdx = − kx 22 − kx12
2
2
x
∫
(4)
1
It is interesting to note that this work is only dependent on the two end states, that is, x1 and x2. When this is the case, the force is called
a conservative force. This would not be the case for friction, for example, because the work would depend on the path taken between
points 1 and 2. If we substitute Eqs. 2-4 back into Eq. 1 we get
1
1
1
1
mv 22 − mv12 = − kx 22 − kx 12
2
2
2
2
(5)
The only unknown in this equation is v2, for which we can easily solve.
b) In this part we were told to use a system that includes the spring as shown in the figure to the
right. In this case the energy of the system will be
E sys1 = E k1 + E s1 =
1
1
mv12 + kx 12
2
2
E sys2 = E k 2 + E s 2 =
1
1
mv 22 + kx 22
2
2
mg
kx
N
(6)
(7)
For this system no work is done since the normal force is perpendicular to the motion and the spring force, where we cut the spring at
the wall, does not travel through any distance. Therefore, when we substitute into the conservation of energy equation, we get:
E sys2 − E sys1 = W
1 2 1
1 2
1
2
2
mv 2 + kx 2 − mv1 + kx 1 = 0
2
2
2
2
or rearranging we get
1
1 2
1
2
2 1
2
mv 2 − mv1 + kx 2 − kx 1 = 0
2
2
2
2
(8)
which we can again solve for v2. What I would like to point out is that Eq. 8 and Eq. 5 are exactly the same. The only difference is that
the spring terms are on the right hand side of the equation in Eq. 5 (where we calculated the work of the spring force) and on the left
hand side in Eq. 8 (where we used elastic potential energy).
What do I want you to get from this problem? First, when you have a spring, be careful when defining your system (usually, put the
spring in the system). Second, if you have a conservative force, that is, one where the work done by the force only depends on the end
states, we can always define a potential function and instead of finding the work of the force, we can use the potential energy of the
force and put that term on the other side of the equation. Mathematically, we can say the work of a conservative force is
W = −(V( x 2 , y 2 , z 2 ) − V( x 1 , y1 , z 1 )) = −(V1 − V2 )
2–55
where V is called the potential function. For a linear spring this is obviously equal to
1 2
kx . It turns out the conservative force, F, is
2
equal to the gradient of the potential function, that is
r
r
F = −∇V
r
where the symbol ∇ stands for the vector operator “del”, which is
r
∂ ˆ ∂ ˆ ∂
∇ = ˆi
+ j +k
∂x
∂y
∂z
Example 2/16
Sliders A and B are of equal mass, m = 5 kg, and are confined
to move in the vertical plane through the frictionless guides as shown.
Their connecting link has negligible mass and length L = 1.0 m. The
blocks are released from rest in the position where θ = 30°. The spring,
k = 1000 N/m, is stretched 0.1m when A is released and the force
F = 20 N is constant in magnitude and direction and is applied at the midpoint
of the bar. Determine the velocity of A when θ = 90°.
F
A
θ
L
B
k
Strategy: We should use conservation of energy since we have two definite positions (θ=30° and θ=90°), and we want to determine the
velocity at θ=90°.
When we use conservation of energy, it is often easiest to draw the system in the
two positions. Obviously, we need to first define a system. For this problem, we
will choose the system shown below. We will include both masses and the
connecting rod because then we don’t have to worry about the reactions between the
rod and the sliders - it will be an internal force. We will also include the spring in
the system, so we don’t have to determine the work the spring does. Since it is
inside the system we will take care of it using elastic potential energy.
System
boundary
A
θ
L
We need to draw the system at the two positions we are interested in, so we can
clearly define a datum for the problem as shown.
F
F
k
B
A
θ
L
k
B
Position 1
F
Datum
k
A
B
L
Position 2
Datum
2–56
Conservation of energy is:
E sys2 − E sys1 = W
(1)
Let’s start by determining the work and then we will find the energy at positions 1 and 2. The external forces we have acting on our
system are:
• The normal forces between the sliders and the vertical and horizontal guides. These will do no work since they act
perpendicular to the motion.
• The spring force acting where we cut the spring near the wall. This will also do zero work since it does not travels through a
distance, and
• The force F. This will be the only force that does work.
Work of F
2
r r
W = F ⋅ dr
∫
1
Since F is constant in magnitude and direction, we get
W = Fs where s = -L/2cos30° = -(20 N)(1m/2)cos30° = -8.66 N-m
(2)
Note that the work is negative because the force is acting upwards and the displacement is down. Now let’s find the energy at positions
1 and 2.
Energy at Position 1
E sys1 = E k1 + E g1 + E s1
(3)
E k1 = 0 (released from rest)
(4)
E g1 = m A g(L cos 30°) = (5 kg)(9.81 m/s 2 )(1 m)(cos30°) = 42.479 N - m
(5)
where
E s1 =
1 2 1
kx 1 = (1000 N/m)(0.1 m) 2 = 5.0 N - m
2
2
(6)
Energy at Position 2
E sys2 = E k 2 + E g 2 + E s 2
(7)
where the kinetic energy is
E k2 =
1
1
1
1
m A v 2A + m B v 2B = m A v 2A = (5)( v 2A ) = 2.5v 2A
2
2
2
2
(8)
The velocity of B will be zero at position 2 since it is at this point that B will change directions. The gravitational potential energy will
be zero since both A and B are at the datum when the system is at position 2,
E g2 = 0
(9)
The spring energy is
E s2 =
1 2 1
kx 2 = (1000 N/m)(0.1 m - 0.5sin30°) 2 = 11.25 N - m
2
2
(10)
2–57
With spring energy, the question you should always ask yourself is, “How much is the spring stretched or compressed from its free
length?” In this problem we are told it is stretched 0.1 m in position 1. At position 2, mass B will move L/2sin30° to the right, meaning
the spring will now be compressed 0.1 – 0.5sin30°. Since we square the displacement, the spring energy will always be positive,
whether the spring is in compression or tension. The only energy term that might be negative is gravitational potential energy since it is
measured with respect to some arbitrary datum.
Substituting Eqs. 2-10 into Eq. 1 we get:
E sys2 − E sys1 = W
(2.5v 2A
+ 0 + 11.25) − (0 + 42.479 + 5) = −8.66
Solving for the velocity of A we get:
v 2A =
−8.66 + 42.479 + 5 − 11.25
= 11.068
→ vA = 3.33 m/s
2.5
What would change if I had told you the applied force was 200 N rather than 20 N? The only thing that would change is the work,
which would be 10 times larger or -86.6 N-m. So what? If you look at the velocity of A shown above, if we change the -8.66 to -86.6
we will get
v 2A =
−86.6 + 42.479 + 5 − 11.25
= −20.15
2.5
If we take the square root of this we get a complex quantity! What does this mean? Where did we go wrong? Our problem was at the
very beginning when we defined positions 1 and 2. We assumed the system would actually get to position 2! If you ever get an answer
that makes no sense, like a complex velocity, it may be that you have an incorrect assumption. In the case where F = 200 N, it makes no
sense to ask the velocity of A when θ = 90° since it will never reach that point. I would probably change the problem and ask you to
find the maximum angle θ. How could we make this problem considerably harder? Easy, I could tell you that the small rollers lock up,
so instead of having essentially frictionless guides, the blocks would slide along the slots. There would now be a friction force acting on
each block equal to µkN. Why is this much harder? Because the friction force will depend on the displacement, so if you want to find
the work of the friction force as block A or B moves from position 1 to position 2, you will need to calculate the integral. For example,
for block B we would have
2
r r
WB = F ⋅ d r
∫
1
x2
∫
→ - µ k N( x )dx
x1
and you would need to determine the normal force as a function of x. To do this, you need to use conservation of linear momentum.
2–58
Example 2/17 Picking your system carefully.
The 5 kg collar A slides with negligible friction on the fixed vertical shaft.
When the collar is released from rest at the bottom position shown, it
moves up the shaft under the action of the constant force F = 200 N applied
to the cable. Determine the spring stiffness if the mass is found to have a
velocity of 1 m/s when the spring is compressed 75 mm. The position of
the small pulley B is fixed.
400 mm
k
F
B
450 mm
75 mm
A
Strategy: We have two definite positions and we are given a velocity, so let’s use conservation of energy. The first thing we need to
decide is what system to pick. I can think of three choices as shown:
F
B
F
B
System 3
System 2
System 1
A
F
B
A
A
Which one should we use? You can solve the problem using any of them, but it turns out that some systems make the problem harder
than others. I am going to suggest that we use system 3, for the following reasons:
For System 1 we can make the following observations:
Objection 1: The spring is outside the system boundary, so it will apply an external force on the system and we will have to find the
work the spring force does, which will involve taking an integral. This is not hard to do, but I prefer to deal with elastic potential
energy.
Objection 2: The tension in the rope is F, but for the System 1 only the component of F in the direction of the motion will do work.
This component is continually changing directions, so again we will need to do an integral.
For System 2 we have included the spring in the system. This takes care of objection 1, but not objection 2, that is, it is still not easy to
find the tension in the rope where the system boundary cuts it.
For System 3, we have the spring in the system and the work the force F does will just be the magnitude of F (since it is constant) times
the distance the force travels. So, we’ll solve the problem using System 3. To start, let’s draw the system in the two positions as shown
below. Since the figure will be very cluttered if I draw the two positions on the same figure, I will draw them side by side.
400 mm
k
400 mm
B
k
F
B
75 mm
450 mm
75 mm
450 mm
A
Position 1
datum
A
Position 2
F
2–59
Applying conservation of energy we get
E sys2 − E sys1 = W
(1)
Let’s start by determining the work, since this is the hardest part of this problem, and then we will find the energy at positions 1 and 2.
The external forces we have acting on our system are:
• The normal force between A and the vertical guide. This force will do no work since it acts perpendicular to the motion.
• The reactions at the pulley B. Again, these will do no work since they do not travel through a distance.
• The spring force acting where we cut the spring near the wall. This force will do zero work since it does not travels through a
distance, and
• The force F. This will be the only force that does work.
Work of F
2
r r
W = F ⋅ d r = Fs (since F is a constant force)
∫
1
where s is the distance the force F travels. From the figure it is clear that the distance F travels will simply be the amount of rope that
goes over the pulley at B, that is
s = 0.4 2 + 0.45 2 − 0.4 = 0.2021 m
so
W = Fs = (200 N)(.2021 m) = 40.42 J
(2)
Note that the work is positive because the force and the displacement are in the same direction. Now let’s find the energy at positions 1
and 2.
Energy at Position 1
E sys1 = E k1 + E g1 + E s1
where
E k1 = 0 (released from rest)
E g1 = 0 (at the datum)
E s1 = 0 (spring is initially unstretched)
so
E sys1 = 0
(3)
Energy at Position 2
E sys2 = E k 2 + E g 2 + E s 2
where
1
1
mv 2 = (5 kg)(1 m/s) 2 = 2.5 J
2
2
= mgz 2 = (5 kg)(9.81 m/s 2 )(0.45 m) = 22.07 J
E k2 =
E g2
E s2 =
1 2 1
kx 2 = (k )(.075) 2 = 0.00281k
2
2
so
E sys2 = 2.5 + 22.07 + 0.00281k = 24.57 + 0.00281k
(4)
2–60
Substituting Eq. 2-4 into Eq. 1 we get
(24.57 + 0.00281k ) − 0 = 40.42
→
k = 5,640 N/m
What if the force had only been 20 N instead of 200 N? The work would have been a factor of 10 smaller (4.04 J) and we would have
calculated a negative value for k. What does this mean? We’ve seen this type of nonsensical answer before, so you should know. Yep,
it means we have an assumption that is wrong, in this case that it will have a velocity of 1 m/s at position 2 or that it will even reach
position 2 at all.
What if I had asked you to solve this problem using the system we called “System 2” above? What would change? The only thing that
would change would be the work. Let’s see how we would calculate it in this case. Let’s look at a FBD at some intermediate position,
that is, displaced up a distance x.
θ
Remember, we don’t need to find the work of the weight since we moved that term to the other side
of the equation and are considering gravitational potential energy. The work of the only external
contact force, F, will be
2
r r
W = F ⋅ dr =
∫
x2
∫
0.45
Fx dx =
x1
1
∫ F cos θdx
F
A
x
mg
0
To do this integral we need to know θ as a function of x. From geometry we can write
tan θ =
0.4
0.4
→ θ = tan −1
0.45 − x
0.45 − x
so
0.45
W=
∫ F cos tan
0
−1
0.4
0.45 − x
dx
There may be some algebraic or trig identities to make this integral look nicer, but who cares, let’s let Maple solve it as shown below. It
is also interesting to note that Maple does express the cos(tan-1( ) term) as an algebraic expression.
> F:=200;
inside:=cos(arctan(0.4/(0.45-x)));
inside :=
F := 200
1
1+
> int(F*inside,x=0..0.45);
0.16
( 0.45 − x )2
40.41594579
This is the same value we had calculated earlier for the work. Is there any advantage to doing it this way? Not really, unless you enjoy
integration, which I have to admit, is always quite fun. The only reason you may want to pay attention to this approach is my next
“what if”. What if I told you there was friction between the bar and A? Assume I give you the coefficient of friction, µ. What changes
now? We have another work term to worry about, that is, the work of friction. The FBD we have in this case is shown below.
θ
Applying linear momentum in the horizontal direction, positive to the right, we get
r
dPsys
dt
=
∑F
→ 0 = F sin θ − N
→ N = F sin θ
so the work due to the friction force will be
F
N
A
x
µkN
mg
2–61
2
x
1
x1
0.45
2
r r
W = F ⋅ d r = − µ k Ndx = − µ k F sin θdx
∫
∫
0.45
=−
∫µ
k F sin
tan
0
∫
0
−1
0.4
0.45 − x
dx
We can again do this integral using Maple in the same way we did earlier. So, in the case of a vertical guide with friction, there is no
way to avoid doing a rather messy integral when we use conservation of energy.
Example 2/18
Initially block A and cart B are stationary and positioned as
shown in the figure. A is released from rest and slides on B.
Assume that all the surfaces in the problem are frictionless and
that right side of the cart is horizontal. Block A drops a distance h
before leaving B.
Block A
µk=0
Cart B
h
Find the velocity of block A and cart B immediately after A leaves B.
Express your answer in terms of mA, mB, g, and h.
Strategy: We have two positions and we want to find the velocity, so let’s use conservation of energy.
For our system we will choose both objects, and as usual, we will start by
drawing the system in the two positions of interest. Position 1 is drawn with
solid lines and position 2 is drawn with dotted lines.
Position 2
Position 1
h
Applying conservation of energy we get
datum
E sys2 − E sys1 = W
Let’s start by determining the work.
Work
The only external forces we have acting on our system are the normal forces between the cart and the ground. These forces will do no
work since they act perpendicular to the motion. Therefore, for this system, the work is zero.
W=0
Energy at Position 1
E sys1 = E k1 + E g1
where
E k1 = 0 (both masses released from rest)
E g1 = m A gh
so
E sys1 = m A gh
Energy at Position 2
E sys2 = E k 2 + E g 2
where
2–62
1
1
m A v 2A + m B v 2B
2
2
=0
E k2 =
E g2
so
E sys2 =
1
1
m A v 2A + m B v 2B
2
2
Substituting the initial energy, the final energy and the work into the conservation of energy equation we get
1
1
m A v 2A + m B v 2B − m A gh = 0
2
2
(1)
We have one equation and two unknowns (vA, vB). How do we get more equations? Let me tell you two things you can’t do, but some
students are tempted to do.
1. You can’t say vB = 0. I only mention this because some students are tempted to do this.
2. You can’t pick another system, that is, A or B by themselves. In general, this is not a bad approach; you need more equations,
so pick another system. If you tried to do that for this problem what would you get? Let’s do it. If we pick A as our system we
would have the two positions shown. I have also drawn A at an intermediate position so
Position 1
we can see the contact forces acting on it. I’m assuming you could easily find the initial
and the final energy. The problem is how do you determine the work? The only external
contact force acting on A will be the normal force, N. In every problem we have had so
far that had a normal force, we said the work of the normal force is zero since it is
Intermediate
h
position
perpendicular to the motion. That is not true in this case! If B was fixed, it would be
true, but since the ramp moves, the normal force will travel through a distance and will do
N
datum
work. How do we calculate this work? Who knows! Looks like a pain to me! So, let’s
Position 2
look someplace else for more equations.
We have decided that we don’t have any more systems that will help us, so what do we do now? You should be asking yourself, are
there any more principles we can use? Of course there are! We still have conservation of LM and AM rate or LM and AM finite.
In this case since we have two definite times, let’s use LM finite.
r
r
Psys2 − Psys1 =
t2
r
∫ ∑ Fdt
t1
Let’s draw some impulse-momentum diagrams.
A
∫m
A
mBvB
B
mAvA
B
B
∫ N dt
1
Momentum after time
interval
Momentum before time
interval
∫m
B gdt
A gdt
A
∫N
2 dt
Impulses during time
interval
Applying the finite time form of LM (positive to the right) we get
−m B v B + m A v A − 0 = 0
We now have 2 equations and 2 unknowns and we can solve for vA and vB! We get
(2)
2–63
vA = mB
2gh
m 2B
+ mAmB
(to the right),
vB = mA
2gh
m 2B
+ mAmB
(to the left)
What would happen if we changed the problem slightly? What if
Block A
B had a lip so that A, instead of flying off into space, hit and stuck
to B? A modified figure is shown. Can we still use conservation
of energy? Of course! The question is what are my two
µk=0
Cart B
times/positions? Can we use conservation of energy from when A
h
and B are initially released to the point after the impact when they
have the same velocity? No! No! No! You may be saying to
yourself, “Why not? I thought energy was always conserved!” I
would reply, “It is!” The problem is that when you have an
impact, there is one other term in the energy equation you need to
worry about, and that is the internal energy, U. So far, the change in internal energy has been zero for every problem we have looked at,
but it is not zero when you have an impact! The bottom line: Don’t use conservation of energy through an impact! So, what would
we do? The problem would be exactly the same as the one we just solved up until the impact. In other words, we would use the
following:
1. Conservation of energy from the time A is released until immediately before impact.
2. Conservation of linear momentum (finite time) from when A is released until immediately before impact
And finally,
3. Conservation of linear momentum (finite time) for the times immediately before impact to immediately after impact.
We have already done step 1 and 2, so let’s do step 3. Once again, let’s draw impulse-mometum diagrams. I’ve replaced all the
impulses with the average impulses.
m B g∆t
(mA+ mB) v’
B
mBvB
A
A
R 1 ∆t
Momentum right after
impact
m A g∆t
mAvA
Momentum right
before impact
R 2 ∆t
Impulses acting during
the impact
Applying the finite time form of LM (positive to the right) we get
(m A + m B ) v ′ − (−m B v B + m A v A ) = 0
We now have 3 equations (1, 2, 3) and 3 unknowns (vA, vB, and v’), which we can solve.
(3)
2–64
2.6 Summary of the Conservation Principles to be Used
In this chapter we have discussed some very basic kinematic relationships and the
conservation principles we will use throughout the remainder of this book. This
section is intended to be a review of this chapter. Almost everything presented in
this section has been discussed earlier in this chapter. The only exceptions are
Table 2.5 and Figure 2.16. The basic principles we will be using in this book are
conservation of linear momentum, conservation of angular momentum and
conservation of energy. The rate forms of these principles are shown below.
r
dPsys
Linear Momentum:
dt
=
r
∑ F +∑ m& v −∑ m& v
r
r
i i
in
o o
(2.14)
out
where
r
r
Psys = mvG = linear momentum of the system. For a system containing several
r
objects Psys =
n
∑ (mv
r
G )i
i =1
m = mass of the system
vG = velocity of the center of gravity
n = number of objects
r
F = external forces
& i = mass flow entering the system
m
r
v i = velocity of mass entering the system
& o = mass flow exiting the system
m
r
vo = velocity of mass exiting the system
r
& i vi = rate of momentum transfer into the system by mass flow
m
r
& o vo = rate of momentum transfer out of the system by mass flow
m
Angular Momentum about point O:
r
dLsys0
dt
=
r
∑ M +∑ r × m& v −∑ r × m& v
r
o
in
r
r
i i
r
(2.23)
o o
out
where
r
L syso = angular momentum of the system about point O (if the system is a single
v
r r
r
rigid body undergoing plane motion L syso = I G ω + rG / o × mv G )
r
M o = external moment about point O
Energy:
dE sys
dt
where
& +W
& +
=Q
∑
in
v2
& i h +
m
+ gz −
2
i
∑
out
v2
& o h +
m
+ gz
2
o
(2.25)
2–65
E sys = E k + E G + E e + U + ... (that is, system energy = kinetic energy +
gravitational energy + elastic energy + internal energy + ...)
& = rate of heat transfer into the system
Q
& = power into the system
W
h = specific enthalpy
zi = vertical distance of the inlet from an arbitrary datum
zo = vertical distance of the outlet from an arbitrary datum
In this book we will primarily, but not always, look at closed systems so Eqs 2.14,
2.23, and 2.25 become:
Linear Momentum:
Key kinetics
concepts for
closed systems
Angular Momentum
Energy:
r
dPsys
dt
=
r
dL sys0
dt
dE sys
dt
r
∑F
=
(2.16)
r
∑M
&
=W
o
integrate
→ ∆E sys = W
(2.24)
(2.26)
In most dynamics books, Eqs. 2.16 and 2.24 are referred to as direct applications of
Newton’s 2nd Law, the finite time forms of Eqs. 2.16 and 2.24 are referred to as
impulse-momentum methods and the finite time form of Eq. 2.26 is referred to as
the work-energy method. You should be comfortable using either name.
A summary of the equations you are expected to know from this chapter and how
they are typically referred to in dynamics textbooks are shown in Table 2.5. Table
2.5 will be very useful in this book in helping you determine which principle to use
when solving a problem. An alternative way of showing this information is the
concept map shown in Figure 2.16. The next few subsections will provide more
detailed procedures to apply depending on which principle you decide to use.
2–66
Table 2.5 - Conservation principles as typically used in Mechanical Systems
Principle
r
dPsys
dt
r
F
=
∑
=
∑M
dt
r
dL sys0
ES201 Name
r
o
Dynamics
Name
Rate form for
conservation of
linear and angular
momentum for a
closed system.
Direct
application
of Newton’s
2nd Law
Finite time form
of conservation of
linear and angular
momentum for a
closed system.
Impulsemomentum
methods
Finite time form
of conservation of
energy for an
adiabatic closed
system.
Workenergy
method.
t
2
r
r
∆Psys = Fdt
∫
t1
t2
r
r
∆L sys0 = M 0 dt
∫
t1
or if there are impulsive loads
acting on the system
r
∆Psys =
r
∆L sys0
Comments
When to use:
want to find forces and/or accelerations
want to find velocities and/or distance
traveled (which can be found by
separating variables and integrating
the basic kinematic relationships)
Other:
Be careful! These are vector equations.
When to use:
have an impact or impulsive forces
the system consists of several objects
given a force as a function of time
want to find velocities, times, or forces
(especially impulsive forces)
Other:
Be careful! These are vector equations.
r
∑rF ∆t
= ∑ ( M ) ∆t
i
0 i
where Fi and Mi are only
external impulsive forces and
moments acting on the system.
∆E sys = W
Key steps in applying
conservation principles
When to use:
have two locations in space
given a force as a function of position
want to find velocities, distances, or
forces (sometimes)
Other:
This is a scalar equation.
Recall that the key steps in applying a conservation principle are:
1. Identify the system
2. Identify the property to be counted
3. Identify the time interval, that is, do you want the rate form or finite time form
of the conservation principle?
2–67
Kinetics
Conservation Principle:
Rate form of conservation of linear
and angular momentum
Finite time form of
conservation of energy
Finite time form of conservation of
linear and angular momentum
- have two locations in space
- have an impact or impulsive forces
- want to find velocities, distances,
and sometimes forces
- are considering several objects that
are interacting
- given a force as a function of
displacement
- given force as a function of time
Clues as to when to use:
- want to find forces and/or
accelerations
- want to find velocities and/or
distance traveled (which can be
found by separating variables and
integrating the kinematic
relationships for a or α ).
- want to find velocities, times,
forces (especially impulsive
forces)
Procedure:
Define the system
Draw FBD and KD
Define a coordinate system
Apply the principle
Check to make sure there are
enough equations
Define the system
Draw the system in two locations
Define a coordinate system
Apply the principle
Check to make sure there are
enough equations
Define the system
Draw impulse-momentum
diagrams
Define a coordinate system
Apply the principle
Check to make sure there are enough
equations
Figure 2.16 - Concept map of conservation principles, clues when to use and brief procedures
It is often possible to solve a problem using more than one conservation principle,
that is, there is often not a unique solution to a problem. For example, you may
solve a problem using conservation of energy or conservation of linear momentum
(rate form). Even though there is not a unique solution, often one of the principles
will be easier to apply than the others. The purpose of the “when to use” sections
of Table 2.1 and Figure 2.16 are to help you to identify which principle to try first.
The next few sections give some procedures to use when applying these principles
to particles. They have all been presented earlier in this chapter, but I wanted to
collect them in one place. We will add to these procedures when we discuss rigid
bodies.
2–68
2.6.1 Procedure for applying the rate form of
conservation of linear momentum (Newton’s 2nd law) to
particles
After deciding that you should use the rate form of conservation of linear
momentum to solve a problem (we usually don’t use the rate form of angular
momentum for particles), what do you do? As shown in Table 2.5 and Figure 2.16,
you should use this principle when you want to find forces and/or accelerations.
You can still use this principle to find velocities and distances, but you will first
need to find the accelerations and then integrate. The following procedure is
intended to give you a methodic approach when solving problems of this type.
Don’t try to use your intuition or skip steps. Good engineering communication
requires you to show all of your work and for it to be neat and organized so it is
easy for someone else to understand what you are doing. This includes drawing
figures and stating what you are doing.
1.
Kinetic
Diagram (KD)
Free Body
Diagram (FBD)
2.
3.
ma G 2
F2
W
4.
5.
F1
Identify the system. The system you pick usually involves the forces and/or
accelerations in the find statement.
Draw the free body diagram (FBD). Include all external forces and moments.
Don’t forget gravity.
Draw the kinetic diagram (KD). In this diagram you put all of your mass times
r
acceleration terms. For plane motion be sure to include ma G . The constraints
r
on the problem may permit you to limit the direction of a .
Place a coordinate system between the FBD and KD to be used when applying
conservation of linear momentum.
Apply the scalar equations for conservation of linear and angular momentum to
the FBD and KD. Be sure to define a positive direction for the summations.
dPsys x
dt
6.
=
∑F
x
,
dPsys y
dt
=
∑F
y
Solve the equations for the required unknowns. If the two scalar equations
have more than two unknowns, then a kinematic analysis may be required for
the problem solution. If you still need more equations after a kinematic
analysis, then try another FBD/KD of an interrelated system.
2.6.2 Procedure for applying the finite time form of
conservation of energy to particles
As shown in Table 2.5 and Figure 2.16 when you have a problem involving two
locations in space, you want to find velocities, distances or forces that do work, or
are given a force as a function of displacement, then the finite time form of
conservation of energy is often the principle to try first. A procedure for this
principle is shown below.
1.
2.
3.
4.
Identify the system.
Draw diagrams of the system in position 1 and position 2.
Locate a datum (if any center of gravity changes elevation).
Calculate each term in the energy equation.
2–69
Principle:
∆E sys = W
where:
W = work of all external forces and moments
2
r r
for a force: W = F ⋅ d r
∫
1
Esys = Ek + EG + Es + U ...
1
mv G2 for each particle in the system
2
EG = gravitational potential energy = mgz for each particle in the system
(Note: z is measured from the datum to the center of gravity).
1
Es = elastic potential energy for a linear spring = kx 2 for each spring in
2
the system
(Note: x is measured from the free length of the spring).
Ek = kinetic energy =
2.6.3 Procedure for applying the conservation of linear
momentum (finite time form) to particles
Clues as to when to use the finite
time form of linear momentum
The finite time form of linear momentum (LM finite) is usually used when you:
1. have a problem involving impacts,
2. have two specific times,
3. have several interacting bodies and you do not know (or care about) the
internal forces,
4. are given a force as a function of time,
5. want to find times, forces (especially impulsive forces), or velocities.
Just like LM rate, the finite time form of LM is a vector equation so we will
emphasize drawing pictures, called impulse momentum diagrams. A complete
procedure is shown below.
Procedure
1. Identify the system. For impact problems you often start by picking both
objects as your system.
2. Draw impulse-momentum diagrams.
mvG 2
mv G1
=
System momentum after
the time interval
System momentum
before the time interval
∫ F dt
1
∫ F dt
2
Impulses acting during the time
interval
2–70
3.
4.
Define a coordinate system to be used when applying conservation of linear
momentum.
Apply the scalar equations for conservation of linear momentum to the
impulse-momentum diagrams. We therefore have two scalar equations
1. Linear momentum in the x-direction
2. Linear momentum in the y-direction
t
2
r
r
∆Psys = Fdt
∫
t1
or if there are impulsive loads acting on the system
r
∆Psys =
r
∑ F ∆t
i
It is important to note that these are vector equations, so just like the rate form we
can obtain scalar equations by looking at the linear momentum in the x and y
directions and the angular momentum about some point.
5.
Solve the equations for the required unknowns. If the two scalar equations
have more than two unknowns, then a kinematic analysis may be required for
the problem solution. If you have an impact, then you may need to use the
coefficient of restitution equation (Section 3.4). If you still need more
equations try looking at an interrelated system.
Notes:
• If there are impulsive forces acting in the system you can neglect nonimpulsive forces.
• This principle is useful for central force problems.
2-71
Problems
Problem 2.1
Problem 13.1 (taken from Fundamentals of Fluid
Mechanics by Munson, Young and Okiishi)
A vertical, circular cross-sectional jet of air strikes a
conical deflector as indicated in the figure. A vertical
anchoring force of 0.1 N is required to hold the deflector
in place. Determine the mass (kg) of the deflector. The
magnitude of the air velocity remains constant and the
density of air is 1.23 kg/m3.
Problem 2.3
The resistance R to penetration of a 0.25 kg projectile
fired with a velocity of 600 m/s into a certain block of
fibrous material is shown in the graph below. Represent
this resistance by the dashed line and compute the velocity
of the projectile for the instant when x = 25 mm if the
projectile is brought to rest after a total penetration of 75
mm.
R (N)
Rmax
x
Problem 2.2
The conveyor belt shown below moves a constant speed
of vo = 24 ft/s.
Determine the angle α for which the sand is deposited on
the stockpile at B.
If the sand falls with practically zero velocity onto the
& as shown below, determine
conveyor at a constant rate m
the magnitude of the net force P required to maintain a
constant belt speed v (use the smaller of the two angles
from part a). Note: P would not act at the location shown
below - it is placed there for convenience only. Assume
you can neglect the mass of the belt, but not the mass of
the sand on the belt. L = 20 ft.
vo
75
Problem 2.4
A 125 lb block initially at rest is acted upon by a force P
which varies as shown. Knowing that the coefficients of
friction between the block and the horizontal surface are
P (lbf)
125 lb
100
A
15 ft
B
α
L
0
P
25 ft
8
16
Time (s)
µs =0.50 and µk = 0.40, determine,
a) the time at which the block will start moving
b) the maximum velocity reached by the block
c) the time at which the block will stop moving.
P
x (mm)
2-72
Problem 2.5
Boxes A and B are at rest on a conveyor belt that is
initially at rest. The belt suddenly started in an upward
direction so that slipping occurs between the belt and the
boxes. The coefficients of kinetic friction between the
belt and the boxes are (µk)A = 0.30 and (µk)B = 0.32.
Determine the initial acceleration of each box.
If the two block remain in contact how long will it take
them to travel 3 ft? If they separate, what will the
distance between the two blocks be after A has traveled up
the incline 3 ft?
80 lb
100 lb
B
A
Problem 2.8 (modified version of a problem taken from
Vector Mechanics for Engineers by Beer and Johnson)
At an intersection car B was traveling south and car A was
traveling 30 degrees north of east when they slammed into
each other. Upon investigation it was found that after the
crash the two cars got stuck and skidded off at an angle of
10 degrees north of east. Each driver clamined that he
was going at the speed limit of 50 km/h and that he tried
to slow down but couldn’t avoid the crash because the
otehr driver was going a lot faster. Knowing the mass of
the two cars A and B were 1500 and 2000 kg,
respectively, determine
a) which car was going faster
b) the speed of the faster car if the slower car was
traveling at the speed limit.
15°
N
Problem 2.6
If the coefficient of kinetic friction between the 20-kg
block A and the 100-kg cart B is 0.50, and the coefficient
of static friction is 0.55, determine the acceleration of
each block when:
a)
P=40 N,
b)
P=60 N,
c)
P=100 N.
(Hint: To determine it A slides on B assume that it
doesn’t, solve for the friction force and compare to µsN)
A
B
P
20 kg
100 kg
Problem 2.7 (modified version of a problem taken from
Vector Mechanics for Engineers by Beer and Johnson)
A 10 kg package drops from a chute into a 25-kg cart with
a velocity of 3 m/s. Knowing that the cart is initially at
rest and can roll freely, determine,
a) the final velocity of the cart
b) the impulse exerted by the cart on the package.
3 m/s
30°
v
10°
B
A
vA
30°
vB
Problem 2.9 (modified version of a problem taken from
Vector Mechanics for Engineers by Beer and Johnson)
A mother and her child are skiing together, with the
mother holding the end of a rope tied to the child’s waist.
They are moving at a speed of 7.2 km/h on a flat portion
of the ski trail when the mother observes that they are
approaching a steep descent. She decides to pull on the
rope to decrease her child’s speed. Knowing that this
maneuver causes the child’s speed to be cut in half in 3 s
and neglecting friction, determine
a) the mothers speed at the end of the 3-s interval
b) the average value of the tension in the rope during that
time interval.
55 kg
20 kg
2-73
Problem 2.10
A 0.02 kg bullet strikes block A with a velocity of v0 =
150 m/s as shown below. The masses of the blocks are
given in the figure. Assume the bullet becomes lodged in
A and the time of impact is very small. Determine:
a) the velocity of A after the impact
b) the acceleration of A and C after the impact
c) the time it will take for block C to stop sliding on
block A (assume block A is large enough so that C
will not fall off of it.
Problem 2.12
A ball with mass m = 5 lbm is mounted on a horizontal
rod that is free to rotate about a vertical shaft as shown in
the figure. In the position shown (position A), the rod
rotates and the ball is held by a cord attached to the shaft.
In this state, the speed of the ball is V1 = 24 in/s. The cord
is suddenly cut and the ball moves to the position B as the
rod continues to rotate. Neglecting the mass of the rod,
determine the speed of the ball after it has reached the
stop B. Be careful to show all of your work.
Hints:
• The friction force between the blocks is not an
impulse force.
• There will be sliding between the blocks.
µk = 0.3
mc = 1 kg
mb
30°
v0
C
A
frictionless
mA=3 kg
Problem 2.11
A high speed jet of air issues from the nozzle A with a
velocity of 240 m/s and mass flow rate of 0.36 kg/s and
impinges on the vane OB, shown on its edge view. The
vane and its right angle extension have negligible mass
compared to the attached 6-kg cylinder and are freely
pivoted about a horizontal axis through O.
Determine:
a) the steady state angle θ assumed by the vane with the
horizontal.
b) the reaction forces at O.
Point mass
6 kg
240 mm
very light
(assume
massless)
θ
v=240 m/s
B
v=240 m/s
O
120 mm
A
Problem 2.13 (From Dynamics by Beer and Johnson)
Coal is being discharged from a first conveyor belt at the
rate of 120 kg/s. It is received at A by a second belt
which discharges it again at B. Knowing that v1 = 3 m/s
and
v2 = 4.25 m/s and that the second belt assembly
and the coal it supports have a total mass of 472 kg,
determine horizontal and vertical components of the
reactions at C and D.
2-74
Problem 2.14
A conveyor system is fitted with vertical panels, and a 300
mm rod AB of mass 2.5 kg is lodged between the panel as
shown. Assume all the surfaces are smooth. Knowing the
acceleration of the panel and the rod is 1.5 m/s2 to the left
determine the reactions of the carrier on the rod at C and B.
mrod = 2.5 kg
A
mpanel = 10 kg
Problem 2.17
Packages are thrown down an incline at A with a velocity
of 4 ft/s. The packages slide along the surface ABC to a
conveyor belt which moves with a velocity of 8 ft/s.
Knowing that µk = 0.25 between the packages and the
surface ABC determine the distance d if the packages are
to arrive at C with a velocity of 8 ft/s.
4 ft/s
d
8 ft/s
C
A
C
a
30°
B
200 mm
Problem 2.15 (Modified from Dynamics by Beer and
Johnson)
The forklift shown weighs 2250 lb and is used to lift a
crate of weight W = 2500 lb. The coefficient of static
friction between the crate and the fork lift is 0.3.
Determine:
a) the maximum deceleration the forklift can have for
the crate not to slip
b) the maximum deceleration the forklift can have for
the forklift not to tip.
c) If the truck is moving to the left at a speed of 10 ft/s
when the brakes are applied determine the smallest
distance in which the truck can be brought to a stop if
the crate is not to slide and if the truck is not to tip
forward.
Problem 2.16
In an iron ore mixing operation, a bucket full of ore is
suspended from a traveling crane which moves along a
stationary bridge. The bucket is to swing no more than 4
m horizontally when the crane is brought to a sudden stop.
Determine the maximum allowable speed v of the crane.
stationary bridge
traveling crane
20 ft
B
70°
Problem 2.18
An elastic cable is to be designed for bungee jumping
from a tower 130 ft high. The specifications call for the
cable to be 85 ft long when unstretched, and to stretch to a
total length of 100 ft when a 600 lb weight is attached to it
and dropped from the tower. Determine:
a) the required spring constant k of the cable
b) how close to the ground a 185 lb man will come if he
uses this cable to jump from the tower
c) the maximum acceleration experienced by the man.
bungee
130 ft
Problem 2.19
The 4 lbf object is dropped 5 ft onto the 20 lbf block that
is initially at rest on two springs, each with a stiffness k =
5 lb/in. Calculate the maximum deflection of the springs
assuming the two objects stick together after the impact.
4 lbf
v
pivot
10 m
bucket
20 lbf
k
k
2-75
Problem 2.20
The system is at rest in the position shown, with the 10 kg
collar A resting on the spring
(k = 500 N/m), when a constant 0.5 kN force is applied to
the cable. What is the velocity of the collar when it has
risen 0.2 m? Assume there is no friction between the
vertical shaft and A.
0.5 kN
0.5 m
A
k
0.4 m
Chapter 3 Particle Kinematics and Dynamics
In this chapter we will continue our discussion of particle dynamics by looking at
additional elements of kinematics. We will examine relative motion, dependent
motion, normal and tangential coordinates, radial and transverse coordinates and
impacts (which are not really kinematics, but we’ll put it here for lack of a better
place).
3–2
3.1 Relative Motion
This is one of the most important topics in this course. All motion is relative. We
have to have some frame of reference (coordinate system) in order to measure
position, velocity and acceleration.
For this course, these frames of reference can be divided into two groups. First,
reference points that are fixed, usually with respect to the earth or the laboratory. I
know these frames of reference are moving with respect to the sun and the stars, but
they don't have much acceleration to speak of. It's usually safe to think of them as
"fixed."
Where relative motion
fits in the kinematics
concept map
The second frame of reference is going to be discussed at length in these notes. It
is a reference system that is itself moving.
Let's say that observer A is at the origin of a moving reference frame. He or she
observes the motion of another point B. A can measure a position, velocity and
acceleration for B. But these motions are not the same that an observer in the fixed
frame would measure by observing B. The difference is A's motion. It's common
sense, I hope.
y
A
r
rA
O
B
r
rB / A
Here are the basic relationships, which can be seen in the figure to the left. Note
that to get to point B we can either go there straight from O, or we can go to A first
and then head over to B. This idea can be expressed vectorially as follows:
r
r r
rB = rA + rB / A
r
rB
x
O = origin of fixed coordinate system
A = origin of moving coordinate system
B = another moving point
(3.1)
In words, Eq. 3.1 says that: the position of B is equal to the position of A plus the
relative position of B with respect to A. Now let's differentiate the previous
equation with respect to time. What we obtain is a similar statement about the
velocities.
r
r
r
vB = vA + vB / A
(3.2)
or in words, the velocity of B is equal to the velocity of A plus the relative velocity
of B with respect to A. Now differentiating with respect to time again gives
r
r
r
aB = aA + aB / A
(3.3)
This equation says that the acceleration of A plus the acceleration of B as seen from
A is equal to the acceleration of B measured in the same fixed frame that A's
position is measured in.
For now, we will only consider translating frames and not rotating ones. The topic
of rotating frames will be discussed in the next chapter. The only equations
required to solve problems involving relative motion in this chapter are Eqs. 3.13.3. The following examples illustrate this.
3–3
Example 3/1
There are two escalators, as shown in the figure. Objects A and B are
y
both traveling at constant speeds of 1.5 m/s in the directions shown.
Determine the relative velocity of B with respect to A.
30
30
1.5 m/s
B
A
1.5 m/s
x
Strategy: Use relative motion relationships.
r
r
r
vB = vA + vB / A
We know
(1)
We have two approaches at this point, 1) vector diagram and 2) vector algebra. We will solve the problem both ways to illustrate both
of these approaches.
Vector diagram approach:
r
v A =1.5 m/s
r
v B =1.5 m/s
r
vA
30°
r
vB
30°
r
vB / A
v
Clearly from the diagram and the angles given in the problem this is an equilateral triangle so v B / A = −1.5 m / s ↓
Vector algebra approach: Write all of the velocities in terms of their components and then equate components.
r
r
r
v B = 1.5 cos(30°)ˆi - 1.5sin(30°)ˆj , v A = 1.5 cos(30°)ˆi + 1.5sin(30°)ˆj , v B/A = v B/A x ˆi + v B/A y ˆj
Substituting into the relative velocity equation given by Eq. 1 we get:
1.5 cos(30°)ˆi - 1.5sin(30°)ˆj = 1.5 cos(30°)ˆi + 1.5sin(30°)ˆj + v B/A x ˆi + v B/A y ˆj
Equating components gives:
ˆi : 1.5 cos(30°) = 1.5 cos(30°) + v
→
B/A x
v B/A x = 0
ˆj : - 1.5sin(30°) = 1.5sin(30°) + v
→ v B/A y = −1.5
B/A y
What if the velocity of B was 1 m/s instead of 1.5 m/s? How would the problem change? In this case you can still do either method, but
the vector algebra approach requires less trig. The vector triangle for this problem is shown below. Clearly this triangle is no longer an
equilateral triangle, so you have to use the law of cosines (if you remember it) or what basically turns out to be the vector algebra
r
r
r
approach, that is, the x component of v B / A will be the x component of v A minus the x component of v B .
If you remember the law of cosines then
3–4
r
v A =1.5 m/s
r
v B =1.0 m/s
r
vA
v 2B / A = v 2A + v 2B − 2 v A v B cos(60°)
30°
= 1.52 + 12 − 2(1.5)(1) cos(60°)
= 1.75
r
vB
so v B / A = 1.75 = 1.323 m/s
30°
r
vB / A
This is just the magnitude. To get the direction we would need to use something like the law of sines. As mentioned earlier, if you
don’t remember the law of cosines, then it is still easy to solve the problem. All you need to do is to recognize that the x component of
r
r
r
v B / A will be the x component of v A minus the x component of v B . This can be clearly seen looking at the figure above.
v B / A x = −1.5 cos(30°) + 1cos(30°) = −0.433 m/s
Similarly for the y components
v B / A y = −1.5 sin(30°) − 1sin(30°) = −1.25 m/s
This last approach of looking at the components is obviously just the vector algebra approach as shown below.
Vector algebra approach: Write all of the velocities in terms of their components and then equate components.
r
r
r
v B = 1.0 cos(30°)ˆi - 1.0sin(30°)ˆj , v A = 1.5 cos(30°)ˆi + 1.5sin(30°)ˆj , v B/A = v B/A x ˆi + v B/Ay ˆj
Substituting into the relative velocity equation given by Eq. 1 we get:
1.0 cos(30°)ˆi - 1.0sin(30°)ˆj = 1.5 cos(30°)ˆi + 1.5sin(30°)ˆj + v B/A x ˆi + v B/Ayˆj
Equating components gives:
ˆi : 1.0 cos(30°) = 1.5 cos(30°) + v
→
B/A x
v B/A x = −0.433 m/s
ˆj : - 1.0sin(30°) = 1.5sin(30°) + v
→ v B/Ay = −1.25 m/s
B/Ay
Example 3/2
A police car is entering a highway at 35 mph when he takes a radar reading of a car traveling on the highway. The radar gun reads 75
mph. Assuming the radar gun gives the magnitude of the relative velocity between the two cars, what is the actual velocity of the car in
mph?
Police car
Strategy: Use relative motion equations.
The vector equation relating the motion of the two cars (let’s call the police car A and the other car B) is
r
r
r
vB = vA + vB / A
We have two choices at this point. We could draw the vector triangle or we could use vector algebra. Which one is best? It really
doesn’t matter although usually one of them is easier than the other (it depends on the problem). Let’s do the problem both ways just to
illustrate how.
3–5
Method 1 - Vector Triangle:
We know the direction of both cars and the magnitude of the relative velocity and of the velocity of A. So, we can draw a vector
vB
triangle as shown below.
vA = 35 mph
vB/A = 75 mph
2
2
2
Clearly from this triangle we can use the Pythagorean theorem to get v B
/ A = v A + v B and solve for the velocity of car B.
v B = v 2B / A − v 2A
= (75 mph ) 2 − (35 mph) 2
= 66.3 mph
Method 2 – Vector Algebra:
When using the vector algebra method, let’s just plug everything we know into the vector equation and see if we get enough equations to
solve for our unknowns. We’ll use the standard x-y coordinate system shown.
r
r
r
vB = vA + vB / A
− v ˆi = −35ˆj + v
B
ˆj
ˆi
ˆ
ˆ
B / A x i + vB / A y j
Equating components we get
ˆi :
− v B = v B / Ax
(1)
ˆj :
0 = v B / Ay
(2)
Well, we now have 2 equations and 3 unknowns. Fortunately, we also have one more equation because we know the magnitude of the
relative velocity, that is:
v B / A = 75 =
(v B / A )2 + (v B / A )2
x
y
(3)
We now have three equations and three unknowns and can solve these three equations (by hand or using Maple).
Example 3/3
A toy car is propelled by water that squirts from an internal
tank at 3 m/s relative to the car. If the mass of the empty car
is 300 g, it holds 1 kg of water, and you neglect other tangential
forces, what is its top speed? Neglect friction and assume the
wheels are small (which basically means to neglect friction
between the tires and the road).
20°
I know, I know. It is a stupid picture, but it
is the best I could find on short notice!
Strategy: Since the car is squirting out water, let’s consider an open system and use LM rate. We also are given a relative velocity, so
we will likely need to use our relative motion equations.
In the problem statement we are given:
v w / c = 3 m/s (velocity of the water with respect to the car)
mc = 0.3 kg (mass of the car)
3–6
LM rate for an open system:
r
dPsys
dt
=
r
∑ F +∑ m& v −∑ m& v
r
r
i i
in
o o
out
To use this we need to draw a KD, FBD and what I like to call the “mass flow diagram.” Again, these are just visual representations of
the conservation principles and help us to apply it correctly (since it is a vector equation).
FBD
KD
& evw
m
mg
Mass flow diagram
θ
d(mvc )
dt
N
Note that the direction of the momentum transfer out is at an angle θ, not 20°. We know the direction of the relative velocity is at 20°,
but we really don’t know the direction of the total velocity.
0
Linear momentum in the x-direction (+ →)
dPsys x
dt
=
0
∑ F +∑ m& v −∑ m& v
x
i ix
in
o ox
out
d(mv c )
& e (− v w )
= −m
x
dt
Take the derivative
dv
dm
& evw
vc + m c = m
x
dt
dt
(1)
At this point we have four unknowns, m (the mass of the car + water), vc (the velocity of the car), v w x (the velocity of the water
& e (the mass flow rate of the water leaving the car). So, we need some more equations.
leaving the car in the x direction, and m
r
r r
v w = vc + v w / c
Relative motion:
Let’s plug in what we know using a standard x-y coordinate system and the directions assumed in the diagrams.
− v w x ˆi + v w y ˆj = v cˆi + (− v w / c cos(20°)ˆi + v w / c sin (20°)ˆj)
Equate components
ˆi :
ˆj :
− v w x = v c − v w / c cos(20°)
(2)
v w y = v w / csin(20°)
We didn’t number the j components since we really don’t care what v w y is. We still need more equations. Hmmm. Since we have
mass flow, let’s use conservation of mass.
0
dm
&i −m
&e
=m
dt
(3)
3–7
OK, now what? We’ve used all of the appropriate conservation principles and we’ve used kinematics. What’s left? Is there anything
else in the problem statement that might be useful? Yes! We know the initial mass of the system, so let’s substitute Eq. 2 and 3 into 1
and integrate.
dm
dv
dm
vc + m c = −
(− vc + v w / c cos(20°))
dt
dt
dt
dm
dm
=
vc −
v w / c cos(20°)
dt
dt
so
m
dvc
dm
=−
v w / c cos(20°)
dt
dt
Now separate variables and integrate assuming the starting mass is mo and the final mass is mf.
∫
vc
0
dv c = − v w / c cos(20°)
∫
mf
mo
dm
m
m
v c = − v w / c cos(20°) ln m m f = − v w / c cos(20°)(ln m f − ln m o )
o
m
= − v w / c cos(20°) ln f
mo
= v w / c cos(20°)ln
mo
mf
Clearly the velocity of the car, vc, will be largest when the final mass is smallest, that is, when all of the water has been expelled.
Substituting in numbers vw/c = 3 m/s, mo = 1.3 kg, mf = 0.3 kg we get
vc = v w / c cos(20°) ln
= 3 cos(20°) ln
mo
mf
1.3
= 4.13 m / s
0.3
3.2 Dependent Motion
Sometimes the motion of two or more objects is related because of a constraint. To
relate the motion of the objects a constraint equation needs to be determined. A
common example of dependent motion is when an inextensible cable connects
objects.
The following procedure is very helpful when approaching problems of this type:
Where dependent
motion fits in the
kinematics concept map
1.
2.
3.
Set up a datum for each position vector and draw the position vectors.
Determine a constraint equation (such as the length of cable connecting the
objects).
Differentiate the constraint equation with respect to time to determine velocity
and acceleration constraint equations.
This procedure is most clearly illustrated by looking at some examples.
3–8
Example 3/4
Two objects are connected by a cable as shown. Determine
the relationship between the accelerations of the two objects.
d = constant
xA
A
yB
B
Strategy: This is a dependent motion problem since the motions of the two objects are related because of the cable. Determine a
constraint equation using the fact that the length of cable remains constant.
Step 1: Define datums and position vectors as shown. Note: This is already done in the figure, but will be the first step on homework
problems.
Step 2: Write a constraint equation: L = 2(d-xA) + yB + constants. Note: We’re not going to worry about all the constants (like the
amount of cable on the pulley) since when we differentiate they will all go to zero.
Step 3: Differentiate: 0 = - 2 vA + vB and if we differentiate again we get 0 = - 2 aA + aB
Comments:
1. Note that in these equations the positive direction for aA and aB are to the right and down respectively. This is important if a
constraint equation is used in conjunction with conservation of linear momentum. For example, if we applied conservation of linear
momentum to block B we would get:
FBD
KD
mBaB
T
Linear momentum in the y-direction (+↓)
r
dPy
mBg
∑
=
Fy
dt
m Ba B = m Bg − T
If up had been defined to be positive in the linear momentum equation, then the equation obtained would be inconsistent with the
constraint relationship derived earlier. The lesson to be learned? Be careful!!
2. This problem probably could have been done by inspection by counting the number of cables associated with each block and then by
reasoning out the kinematic relationship.
3–9
Example 3/5
Three objects are connected by cables as shown. Determine
a relationship between the accelerations of the objects.
Cable 1
yD
yA
yC
A
C
yB
Cable 2
B
Strategy: Determine a constraint equation using the fact that the lengths of the cables remain constant. Note: the first step in any
problem will be to define the coordinates. In this example, this is already done for you (which makes the problem easier), but for
problems you solve on your own, you will need to do this first.
Step 1: The coordinates are defined as shown.
Step 2: Since there are two cables, we will have two equations.
L1 = 2yC + 2yD + constants
L2 = yA + yB + (yB - yD)+ constants
Step 3: Differentiate
→ 0 = 2aC + 2aD
0 = 2vC + 2vD
differentiate again
(1)
→ 0 = aA + 2aB - aD
0 = vA + 2vB - vD
differentiate again
(2)
The acceleration of point D can easily be eliminated from Eqns. 1 and 2, giving a single kinematic relationship between the
accelerations of masses A, B and C:
0 = 2aC + 2aA + 4aB
3–10
Example 3/6
Two objects are connected by a cable and one is moving at a
constant velocity. Determine the velocity of object B as a
function of xA.
H
h
B
VA = constant
yB
A
xA
Strategy: Determine a constraint equation using the fact that the length of the cable remains constant.
Step 1: See illustration for the definition of the coordinates.
Step 2: Constraint equation
L = (H − y B ) + h
= (H − y B ) + H 2 + x 2A
Step 3: Differentiate
0 = -v B +
x A vA
2
H +
x 2A
→ v B =
x AvA
H 2 + x 2A
Example 3/7
A 6-kg block B rests as shown on a 10-kg bracket A. The coefficients of friction are µs = 0.30 and µk = 0.25 between block B and
bracket A, and there is no friction in the pulley or between the bracket and the horizontal surface.
a) Determine the equations necessary to find the maximum mass of block C such that block B does not slide on bracket A and to find
the corresponding accelerations.
b) Determine the numerical answers to part a).
c) If the mass of block C is 10% larger than the maximum such that B does not slide on A, determine the equations necessary to find the
accelerations of A, B and C.
A
B
C
Strategy: Since we want the mass of block C, it looks like we need to use a conservation principle. Which one? Not energy since we
are interested in the object at this instant. Not LM finite because there are no impacts and again we are interested in a particular instant.
Therefore we are left with LM rate form (direct application of Newton’s 2nd Law). We’ll see if we need anything else as we go along,
but it looks like we may have a dependent motion problem on our hands because of the cable.
3–11
Solution to part a)
When we use LM rate, we need free body diagrams and kinetic diagrams. Let’s start with block C (be careful with notation, that is
subscripts, since we have three objects).
System: Block C
A
T
FBD
KD
B
C
mCg
mCaC
r
dPy
Linear momentum in the y-direction (+ ↓)
dt
=
∑F
→
y
mCa C = mCg − T
(1)
We have three unknowns (T, mC and aC) and one equation, so we obviously need more. Where do we look? Pick another system! We
could pick block A, block B or block A and B together. Let’s pick block B.
System: Block B
A
FBD
KD
B
mBaB
C
T
NB
r
dPy
=
dt
r
dPx
=
dt
LM y-direction (+↑):
LM x-direction (+ →):
mBg
FB
∑F
→
0 = N B − m Bg
(2)
∑F
→
m Ba B = FB − T
(3)
y
x
Now we have 3 equations and six unknowns (T, mC, aC, aB, FB, NB ). Let’s look at bracket A.
System: Bracket A
KD
A
mAg
C
LM x-direction (+ →):
T
mAaA
B
LM y-direction (+↑):
T
A
A
r
dPy
∑
Fy → 0 = N A − m A g − N B
=
r
dPx
=
Fx → m A a A = 2T − FB
dt
dt
∑
FBD
FB
NB
NA
(4)
(5)
Now we have 5 equations and 8 unknowns (T, mC, aC, aB, FB, NB, aA, NA). So, we need three more equations. What do we do? We
don’t have any more systems, so we can either look to kinematics or look for more information in the problem statement. For part a) we
were told we want to find the maximum mC so that B does not slip on A. If we assume B is about to slip we get
FB = µs N B
(6)
3–12
Since there is no slipping, we know all of the objects will move together, that is
aA = aB
(7)
aB = aC
(8)
and
We now have 8 equations and 8 unknowns and we can solve in Maple.
Solution to part b) The Maple solution is shown below with the numerical answers.
> mB:=6:
mA:=10:
mu[s]:=0.30:
mu[k]:=0.25:
g:=9.81:
> eq1:=mC*aC=mC*g-T;
eq2:=0=NB-mB*g;
eq3:=mB*aB=FB-T;
eq4:=0=NA-mA*g-NB;
eq5:=mA*aA=2*T-FB;
eq6:=FB=mu[s]*NB;
eq7:=aA=aB;
eq8:=aB=aC;
eq1 := mC aC = 9.81 mC − T
eq2 := 0 = NB − 58.86
eq3 := 6 aB = FB − T
eq4 := 0 = NA − 98.10 − NB
eq5 := 10 aA = 2 T − FB
eq6 := FB = 0.30 NB
eq7 := aA = aB
eq8 := aB = aC
> solve({eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8},{T,mC,aC,aB,FB,NB,aA,NA});
{ mC = 1.425742574, NB = 58.86000000, FB = 17.65800000, NA = 156.9600000, aB = 0.8026363636,
T = 12.84218182, aC = 0.8026363636, aA = 0.8026363636}
Therefore, the maximum mass of block C is mC = 1.42 kg for block B not to slide relative to bracket A.
Solution to part c)
In this part we are told that the mass of C is 1.1 times the answer found in part b). Let’s just call this mC. How does the problem change
from part a)? Equations 1-5 remain the same. We only have 7 unknowns now (since mC is known) so we need 2 more equations. Since
we know there is slipping, we get
FB = µ k N B
(6a)
The motion of the objects will be related because of the cable, so we have a dependent motion problem. Let’s go through our procedure.
The first step is to define coordinates. We have already picked positive directions for each mass when we used Newton’s 2nd law, so we
must be consistent. Therefore we have
D = constant
xB
xA
A
B
yC
C
3–13
The length of cable is:
L = (x B − x A ) + (D − x A ) + y C + constants
When we differentiate this twice we get
0 = −2a A + a B + a C
(7a)
We now have 7 equations (1-5, 6a, 7a) and 7 unknowns (T, aC, aB, FB, NB, aA, NA) and we are done.
Example 3/8
For the system shown, the mass of A is mA and the mass
of B is mB and the applied force is P. Assume the friction
between all surfaces is negligible. Derive the equations
necessary to solve for the tension in the cable and the
accelerations of the two blocks.
B
15°
P
A
Strategy: Since we are asked to find the tension and the accelerations, we will probably need to use direct application of Newton’s 2nd
law, that is, the rate form of conservation of linear and angular momentum. There is also a cable connecting the two objects, so we’ll
likely need to relate the velocity of A and B. Let’s see how it goes and decide if we need anything else as we go along.
We always draw pictures when using LM rate, so let’s start with a KD and a FBD of block A. Note the system boundary.
System boundary
for A
B
15°
P
A
System: Block A
KD
FBD
y
15°
NB
T
x
mAaA
15°
T
T
mAg
P
NA
Note that in the FBD we have assumed that there is no friction in the pulleys. Let’s apply LM.
3–14
r
dPx
=
dt
r
dPy
=
dt
LM x-direction (+ →):
LM y-direction (+↑):
∑F
x
∑F
y
→
m A a A = P − 2T + T cos(15°) − N B sin (15°)
(1)
→
0 = N A − m A g − T sin (15°) − N B cos(15°)
(2)
So we have 2 equations and 4 unknowns (aA, T, NA, NB). We need more equations, so let’s look at another system, that is, block B.
The FBD is fairly straight forward, but the KD is not because the acceleration of B is not down the incline (as many students might be
tempted to say). Why? Because the incline, A, is not fixed! It’s moving. So, since we don’t really know the direction of the
acceleration of block B we’ll just put generic x and y components.
System: Block B
FBD
y
KD
mBg
x
T
a Bx
a By
r
dPx
=
dt
LM x-direction (+ →):
LM y-direction (+↑):
r
dPy
dt
=
∑F
x
∑F
y
→
NB
m B a B x = −T cos(15°) + N B sin (15°)
(3)
− m B a B y = N B cos(15°) − m B g + T sin (15°)
(4)
→
So now we have 4 equations and 6 unknowns (aA, T, NA, NB, aBx, aBy). We need more equations! Where do we look? Right.
Kinematics or the problem statement to see if anything else is given. We said we don’t know the direction of the acceleration of B
because A is moving, but we do know the direction of A with respect to B, that is the relative acceleration, which will be down the
incline (or up the incline, it really doesn’t matter which we assume). So, let’s use the relative acceleration equation.
r
r
r
aB = aA + aB / A
15°
aB/A
Plugging in what we know we get
a B x ˆi − a B y ˆj = a A ˆi + a B / A cos(15°)ˆi − a B / A sin (15°)ˆj
Equating components we get
ˆi :
a B x = a A + a B / A cos(15°)
(5)
ˆj :
− a B y = −a B / A sin (15°)
(6)
Are we done? Not quite, since we have 6 equations and 7 unknowns (aA, T, NA, NB, aBx, aBy, aB/A ). Since the two blocks are connected
by a cable, let’s use dependent motion. The first step is to define position vectors. Note: We can’t just put these in whatever direction
we want! In our equations above we have already defined the relative acceleration aB/A to be down the incline and the acceleration of A
to be to the right. This is shown below.
xB/A
B
15°
A
xA
P
3–15
Step two is to define the constraint equation, in this case, the length of cable (again neglecting the constant lengths).
L = x B / A + 2x A + constants
Differentiating this twice we get
0 = a B / A + 2a A
(7)
So we now have 7 equations and 7 unknowns and are done. We can solve these by hand or using a computer algebra program. Word
processed solutions always look different (and are much longer) than solutions done by hand, so I’ve pasted a copy of my original
solution below so you can see what it looks like.
3.3 Different Coordinate Systems
In this section we will discuss how we can describe the kinematic quantities such as
position, velocity and acceleration in a variety of coordinate systems. We will
review the Cartesian coordinate system and introduce normal and tangential
coordinates and radial and transverse coordinates. The coordinate system you
choose is typically dependent on the information you are given and what you are
asked to find.
3–16
3.3.1 Cartesian Coordinates
Cartesian or rectangular coordinates are what we have been using up to this point,
that is, we break the vectors into components in the x, y and z directions. In this
coordinate system (let’s just consider 2D motion to make the figures clearer) we
can write the position vector as:
r
r = xˆi + yˆj
(3.4)
If we differentiate this we get
Where Cartesian
coordinates fit in the
kinematics concept map
r
v = x& ˆi + y&ˆj = v x ˆi + v y ˆj
r
a = &x&ˆi + &y&ˆj = a x ˆi + a y ˆj
(3.5)
(3.6)
d( )
. All we are
dt
doing is representing vectors in terms of their x and y components as shown in the
figure below. The magnitude of the velocity is called the speed and the direction of
the velocity is tangent to the path. It is important to note that when traveling in a
curved path, the acceleration is not tangent to the path.
.
where the dot indicates a derivative with respect to time, ( ) =
y
y
Path of
particle
A
A
yˆj
A
a y ˆj
v
xˆi
Position
x
ˆj
O ˆi
ˆj
x
Velocity
Path of
particle
v x ˆi
v y ˆj
r
r
ˆj
O ˆi
y
Path of
particle
a
a x ˆi
O ˆi
x
Acceleration
Figure 3.1 - Position, velocity and acceleration represented in Cartesian coordinates.
This is the coordinate system we used for projectile motion and for all of the
problems in ES201.
3.3.2 Normal and Tangential Coordinates
When describing the motion of a point traveling along a curved path it is often
convenient to use a coordinate system attached to the particle with one unit vector
directed tangent to the path, eˆ t , another normal to the path and directed towards the
center of curvature, eˆ n , and finally a unit vector perpendicular to eˆ t and eˆ n called
the binormal unit vector, eˆ b . The plane that contains eˆ t and eˆ n is called the
Where normal and tangential
coordinates fit in the
kinematics concept map
osculating plane. Since the velocity is always tangent to the path of the particle,
the tangential unit vector is easily determined if you know the velocity as shown
below
r
r
v v
eˆ t = r =
v v
3–17
r
where v = v = speed, that is, the magnitude of the velocity. The velocity vector
Direction of
motion
can be represented in this coordinate system as shown in Equation 3.7.
eˆ b
eˆ n
eˆ t
r
v = veˆ t
eˆ b
eˆ n
Path of
particle
Figure 3.2 - Normal and
tangential unit vectors –
attached to the point of
interest
eˆ t
(3.7)
To the astute observer this may not seem that impressive. This equation basically
says that the velocity is equal to the magnitude of the velocity (the speed) times the
direction of the velocity (a unit vector in the tangential direction). This coordinate
system really becomes useful when we take the derivative of this to get the
acceleration. I’ll give you the final result first and then if you are interested you
can look at the derivation.
r
v2
a = v& eˆ t +
eˆ n = a t eˆ t + a n eˆ n
ρ
(3.8)
where
v = speed of the particle
dy 2
1 +
dx
ρ = radius of curvature =
d2y
3/ 2
dx 2
Before we do the derivation, let’s make some observations:
• The acceleration vector always lies in the osculating plane, that is, the plane
defined by eˆ t and eˆ n . Therefore, the acceleration in the binormal direction is
•
•
always zero.
dv
= a t = the time rate of change of the speed. This is the tangential
v& =
dt
component of the acceleration and reflects a change in the speed of the
particle, that is, the particle is speeding up or slowing down. If at > 0, the
particle is speeding up, if at < 0, the particle is slowing down, and if at = 0 the
particle has a constant speed.
v2
= the normal acceleration. This component of the acceleration
an =
ρ
reflects a change in direction and always points towards the center of curvature
(which is obvious if you look at the derivation shown below.) It is important
to note that a particle may have a constant speed and still have an acceleration
because the velocity vector is changing directions.
The magnitude of the acceleration is obviously just the square root of the sum of
the squares,
r
a = a 2t + a 2n
(3.9)
Figure 3.3 shows what the acceleration components of a woman on a roller coaster
at two selected locations. (Note: I am making the person on the roller coaster
a woman because I don't like roller coasters and my wife does). I just don’t
understand what is so great about feeling like your stomach is going to crawl out of
3–18
Direction
of motion
1
at
a
an
a
Speeding
up
an
at 2
Slowing
down
Figure 3.3 – Acceleration of a
person on roller coaster at two
points along the path
your mouth.) As the car starts to move down the hill, as shown in position 1, the
person is speeding up so she has a tangential component in the direction of the
velocity. The normal component of acceleration is perpendicular to the path. At
position two, when the car starts to go up a hill, the car is slowing down, so the
tangential acceleration is directed opposite to the velocity and again, the normal
acceleration is directed towards the center of curvature. The total acceleration is
simply the vector sum of the two components of acceleration. Let’s look at the
derivation of Eq. 3.8.
Warning! Derivation of acceleration in normal and tangential coordinates.
If we take the derivative of Eq. 3.7 we get
r
r dv d ( veˆ t )
a=
=
dt
dt
(3.10)
deˆ
dv
eˆ t + v t
=
dt
dt
So, all we really need to do is figure out how to take the derivative of the tangential
unit vector. The easiest way to do this is to use the chain rule, that is
deˆ t deˆ t dθ ds
=
dt
dθ ds dt
∆θ =
eˆ n eˆ t
ρ
∆s
ρ
∆θ
P2
eˆ n
P1
∆s
eˆ t
Figure 3.4 - Illustration of how
the unit vectors change with θ.
unit circle
eˆ ′t
∆θ
eˆ t
∆eˆ t
Figure 3.5 - Tangential unit
vectors drawn tail to tail. Note
the direction of ∆eˆ t .
(3.11)
We know that ds/dt is simply the speed of the particle, that is
ds
=v
(3.12)
dt
Now all we need to determine is dθ/ds and the derivative of the tangential unit
vector with respect to θ. Let’s first look at dθ/ds. Assume the motion is as shown
in Figure 3.4, and the particle is moving from point P1 to point P2. From this figure
(and knowing the arc length of a line in terms of the radius of curvature and the
angle) we know ∆θ=∆s/ρ. In the limit, and after rearranging a bit, we will get
dθ 1
=
(3.13)
ds ρ
To find the derivative of the tangential unit vector with respect to θ, let’s redraw
the figure and put the unit vectors tail to tail as shown in Figure 3.5. From basic
trig (just bisect the triangle to get two right triangles), we can note that
∆eˆ t = 2 sin(∆θ/2)
so, we can find the magnitude of the derivative of the tangential unit vector with
respect to θ to be
∆eˆ t
deˆ t
2 sin( ∆θ / 2)
sin( ∆θ / 2)
= lim
= lim
= lim
=1
∆θ → 0
dθ ∆θ → 0 ∆θ ∆θ → 0
∆θ
∆θ / 2
From Fig. 3.5 we can easily see that in the limit as ∆θ goes to zero, the direction of
∆eˆ t will be in the normal direction. Therefore we get
deˆ t
= eˆ n
(3.14)
dθ
3–19
Substituting Eqs. 3.12-3.14 into 3.11 we get
deˆ t v
= eˆ n
dt
ρ
(3.15)
Substituting Eq. 3.15 into Eq. 3.10, we have the final equation for representing the
acceleration of a particle in normal and tangential coordinates
r
v2
a = v& eˆ t +
eˆ n
ρ
End of Derivation
Example 3/9
Determine the banking angle θ of the circular track (see the figure)
so that the wheels of the sports car shown will not have to depend
upon friction to prevent the car from sliding either up or down the
curve. The car travels at a constant speed of 100 ft/s. The track radius
is 600 ft.
θ
ρ = 600 ft
Strategy: Since we have forces involved, this is not a pure kinematics problem, so which conservation principle should we use?
Hopefully by now you recognize that we should try LM rate form (direct application of Newton’s 2nd law) and since we are traveling in
a curved path, let’s try normal and tangential coordinates (it helps that in the problem statement we are given ρ!)
Since we are using LM rate, let’s start off with a FBD and a KD. For
the system we will pick the car. The normal direction, n, is directed
towards the center of curvature, the tangential direction (not shown)
would be out of the plane of the paper, and I have labeled the
binormal direction, z.
System: Car
KD
z
mg
FBD
ma
n
Note that we left off the friction force and the acceleration is drawn
towards the center of curvature. Let’s apply conservation of linear
momentum (rate form):
N
θ
LM n-direction (+ →)
r
dPn
=
dt
∑F
n
→
ma = N sin(θ)
(1)
0 = N cos(θ) − mg
(2)
LM z-direction (+↑)
r
dPz
=
dt
∑F
z
→
We now have 2 equations and in these two equations we have 4 unknown quantities, m, N, a and θ. The mass is not a dynamic quantity
so we will never be able to solve for it (unless we are given additional information), so we will just solve the problem in terms of m
which means that we need one more equation. Where do we go? Yep, kinematics. Since the car is traveling in a circle at a constant
velocity we know
a=
v2
ρ
So we now have 3 equations and 3 unknowns that we can solve. We can do this by hand or with Maple. In this problem it is actually
easier to solve the problem by hand (sometimes Maple is tricky when you have a quantity such as sin(θ)).
(3)
3–20
By hand solution: From (3) we get
a = (100ft/s)2/600 ft = 16.67 ft/s2
If we move the mg to the right hand side of Eq. 2 and divide Eq. 1 by Eq 2 we get
ma N sin(θ)
a 16.67ft / s 2
=
→ tan(θ) = =
= 0.518
mg N cos(θ)
g
32.2ft / s 2
Solving for θ we get
θ = tan −1 (0.518) = 27.4o
Example 3/10
A bucket is filled with sand and released from an angle of θ = 0°.
The cable can support a maximum tension of 500 N. Determine the
mass of the sand and the bucket if the cable breaks when θ = 50°.
3m
θ
Strategy: We should probably look at the bucket at 50° since that is where the cable breaks and where we know the tension. Since we
are given the force we should try to use LM rate using normal and tangential coordinates.
For LM rate we always start with a KD and a FBD. We’ll draw these at 50° and then use our principles.
LM n-direction (+
r
dPn
=
dt
∑F
→
n
LM t-direction (+
r
dPt
=
dt
∑F
t
)
→
System = Bucket
KD
2
m
v
= T − mg sin θ (1)
r
man
θ
(2)
T
eˆ n
θ
eˆ t
θ
)
ma t = mg cos θ
FBD
mat
mg
We have 2 equations and 3 unknowns (v, at, m). Where do we look for another equation? Another system? Nope. Kinematics? Nope,
we’ve already substituted the equation for normal acceleration into Eq. 1. Another conservation principle? Yes. We have two locations
in space, so let’s use conservation of energy.
E sys2 − E sys1 = W
Position 1
where
W = 0 (Tension does no work since it is ⊥ to motion)
E sys1 = E g1 = mgr sin θ
r = 3m
θ
Datum
Position 2
3–21
E sys2 = E k 2 =
1
mv 2
2
Substituting into conservation of energy we get
1
mv 2 − mgr sin θ = 0
2
(3)
So we have 3 equations and 3 unknowns (v, at, m). We can use Maple, but the easiest way to solve this is to solve Eq. 3 for the velocity
and substitute into Eq. 1.
v 2 = 2gr sin θ = 2(9.81 m/s)(3 m) sin (50°)
= 45.09 m 2 /s 2
→
v = 6.71 m/s
Substituting into Eq. 1 and solving for m gives
m=
T
2
v
+ g sin θ
r
=
500 N
2
(6.71m/s)
+ 9.81m/s 2 sin (50°)
3m
→
m = 22.18 kg
The Maple solution is shown below:
> r:=3:
g:=9.81:
theta:=50:
thetar:=theta*Pi/180:
T:=500:
> eq1:=m*v^2/r=T-m*g*sin(thetar);
eq2:=m*at=m*g*cos(thetar);
eq3:=1/2*m*v^2-m*g*r*sin(thetar)=0;
m v2
5π
= 500 − 9.81 m sin
3
18
5π
eq2 := m at = 9.81 m cos
18
m v2
5π
eq3 :=
− 29.43 m sin
= 0
2
18
eq1 :=
> solve({eq1,eq3});
{ m = 22.17817345, v = -6.714862316}, { m = 22.17817345, v = 6.714862316}
What if I asked you to use this mass and solve for the tension as a function of the angle, θ, for θ = 0 to 90°? We’ve basically already
solved this. Let’s just use Eqs. 1 and 3 with the two unknowns (T, v) and plot T. The Maple solution is shown below.
>r:=3:
g:=9.81:
m:=22.178:
thetar:=theta*Pi/180:
>eq1:=m*v^2/r=T-m*g*sin(thetar);
eq2:=m*at=m*g*cos(thetar);
eq3:=1/2*m*v^2-m*g*r*sin(thetar)=0;
θπ
eq1 := 7.392666667v2 = T − 217.56618sin
180
θπ
eq2 := 22.178 at = 217.56618cos
180
θπ
eq3 := 11.08900000v2 − 652.69854sin
= 0
180
3–22
>sol1:=solve({eq1,eq3},{v,T});
3
θπ
sol1 := { T = 652.6985400sin( 0.01745329252θ ), v = RootOf 2 _Z 2 − 327 sin
, label = _L3 }
5
180
> T1:=subs(sol1,T);
T1 := 652.6985400sin( 0.01745329252θ )
> plot(T1,theta=0..90);
The previous example problem was fine, but let’s face it, who really cares about a bucket of sand swinging? Let’s look at a similar
problem except in this case it is a matter of life and death and therefore should be significantly more suspenseful. The gist of the
problem? Does Tarzan Save Jane?
Example 3/11 Does Tarzan save Jane?
In order to save Jane from hungry cannibals, Tarzan must
swing over a pit of hungry alligators. He begins swinging
when the vine is horizontal, but alas, he leaped before he
looked, and the vine he is swinging on hits a branch as shown
below. Tarzan has a mass of 90 kg and the vine has a length of 9 m.
Neglect the mass of the vine. Does Tarzan clear the alligator pit
and save Jane? Assume the vine can only support three times
Tarzan's weight. If the vine does not break, assume he lets go
when he is directly below the branch.
L
Tarzan
45°
branch, P
2L
3
2m
Save
me!
10 m
alligator pit
Strategy: We will start by looking at Tarzan after the vine hits the branch, thereby changing the radius of the curvature of the path. We
have two positions, so we will use conservation of energy, and since we need to know if the vine breaks, that is, if the force exceeds
three times Tarzan’s weight, we will use LM rate using normal and tangental coordinates.
Conservation of Energy:
We have two locations in space, so let’s use conservation of energy.
L= 9m
θ=45°
E sys2 − E sys1 = W
where
W = 0 (Tension does no work since it is ⊥ to motion)
E sys1 = E g1 = mgr sin θ
E sys2 = E k 2 =
1
mv 2
2
Substituting into conservation of energy we get
Position 1
Datum
Position 2
3–23
1
mv 2 − mgL sin θ = 0
2
We can easily solve for the velocity
v 2 = 2gL sin θ = 2(9.81 m/s)(9 m) sin (45°)
= 124.86 m 2 /s 2
→
v = 11.174 m/s
Now let’s find the tension immediately before the vine strikes the branch and immediately after (the only difference is that the radius of
curvature changes). To do this, we will use LM rate.
Conservation of Linear Momentum (rate form):
For LM rate we always start with a KD and a FBD. We’ll draw these at
θ = 45° and then use our principles.
LM n-direction (+
r
dPn
=
dt
∑
Fn
man
)
→
System = Tarzan
KD
m
v2
= T − mg sin θ
r
θ
FBD
eˆ n
θ
eˆ t
(1)
T
θ
The only unknown in this equation is T, which we can solve for and
substitute for v
2gL sin θ
v2
= mg sin θ + m
r
r
2L sin θ
= mg sin θ +
r
T = mg sin θ + m
using r = L and r = L/3 (before and after it strikes the branch) we get
2L sin (45°)
Tbefore = mg sin (45°) +
= 2.12mg
L
2L sin (45°)
Tafter = mg sin (45°) +
= 4.95mg
1 / 3L
So, the rope breaks! Does this mean Tarzan dies? Of course not! We are not done with the problem yet. If the rope breaks, he will still
continue moving (he doesn’t just drop straight down), so we have a projectile motion problem to solve. The problem we have now is
shown below.
We can just use our projectile motion equations. In the y-direction we know
y = y 0 + v 0y t −
1 2
gt
2
45°
The first thing we need to determine is how long it takes Tarzan to reach the
ground. If we use the coordinate system shown, we know
y=0
y0 = 10 – 3 sin(45°) = 7.879 m
v 0 y = −11.174 sin (45°) = −7.901 m/s
substituting we get
1
0 = 7.879 − 7.901t − (9.81) t 2
2
3m
10 m
2m
45°
vo=11.174 m/s
y
x
alligator pit
3–24
Solving for t we get t = 0.696 s. In the x-direction the acceleration is zero so
v x = v 0 x = 11.174 cos(45°) = 7.901 m/s
x = x 0 + v 0 x t = 0 + 7.901(0.696) = 5.50 m
So Tarzan will travel 5.50 meters in the horizontal direction before hitting the ground. The end of the alligator pit is 2+3cos(45°)=4.12m
from where Tarzan is when the cable breaks. What does this mean? He clears the pit and saves Jane! I will give you a hint if you face
this type of problem anywhere else in this text. The good guy will always win and we will never kill an innocent creature! If the
question is “Does the car hit the deer?”, the answer will always be “No, of course we will not kill Bambi!” Does Tarzan save Jane?
The answer will always be “Of course he does!”
Example 3/12
A ball is thrown at a speed of 10 m/s at an angle of 30° with respect to the horizontal. What is the radius of curvature of the path of the
ball immediately after it is released and when the ball is at its maximum elevation?
Strategy: What, no picture? The first thing we need to do is to draw a picture. Since we want the radius of curvature, we will probably
need to use normal and tangential coordinates.
10 m/s
30°
The only equation we have discussed so far involving the radius of curvature is
an =
v2
v2
→ ρ =
ρ
an
(1)
So, all we need in order to find the radius of curvature is the normal acceleration. Let’s use LM rate to find the acceleration. Since we
are going to try LM rate, let’s draw a KD and FBD
r
dPy
dt
=
FBD
KD
LM y-direction (+ ↓):
∑F
y
→
ma = mg
a=g
mg
ma
Clearly from LM in the y direction we get that the acceleration of the ball is g down. You probably already knew this since this is just
projectile motion. So, what do we do now? We need the normal component of this acceleration. Do we know the normal direction?
We know it is perpendicular to the tangential direction and we know the tangential direction is in the same direction as the velocity. So,
let’s draw a picture.
eˆ t
Clearly from this picture we can find an = g cos(30°).
Substituting into Eq. 1 we get the radius of curvature when the ball is
is initially released.
ρ=
(10 m/s) 2
v2
=
= 11.77 m
a n 9.81m/s 2 cos(30°)
at
eˆ n
30° an
a=g
3–25
To find the radius of curvature at the maximum elevation, we need the velocity at the maximum elevation and the normal acceleration.
This is simply a projectile motion problem.
vyo = (10m/s)sin(30°)
= 5 m/s
10 m/s
30°
vxo = (10m/s)cos(30°)
= 8.66 m/s
For projectile motion problems we look at the motion in the x and y directions. We know the x component of velocity does not change
(since the acceleration is only in the y direction) and that at the maximum elevation vy = 0. Therefore, at the maximum elevation the
velocity will be 8.66 m/s (directed horizontal) and the normal acceleration will be equal to the total acceleration, g. So, we get
ρ=
v 2 (8.66 m/s) 2
=
= 7.65 m
an
9.81m/s 2
What if I had asked you to plot the radius of curvature as a function of time? Could you do it?
Example 3/13
A bus starts from rest and speeds up at a rate of 5 m/s2 on the
curve as shown. How long will it take for the total acceleration
of the bus to be 10 m/s2.
bus
r = 300 m
Strategy: This looks like a pure kinematics problem since we are not given the mass of the bus or any forces and we’re not asked to find
any forces. Since the bus is traveling in a circle, let’s use normal and tangential coordinates. We are told that the bus speeds up at 5
m/s2, which is the tangential acceleration.
Using normal and tangential components the magnitude of the total acceleration is
a = a 2n + a 2t
So we have one equation and there is one unknown in it, an. Solving for an we get
a n = a 2 − a 2t = (10m / s 2 ) 2 − (5m / s 2 ) 2
= 8.66 m / s 2
This is fine, but what do we do now? Let’s use the equation for normal acceleration to find the velocity of the bus when the total
acceleration is 10 m/s2.
an =
v2
ρ
→ v = a n ρ = (8.66m / s 2 )(300m) = 50.97 m / s
So, all we need to do is to determine how long it will take for the velocity to be 50.97 m/s. Fortunately, we know the tangential
acceleration, which we can integrate.
at =
dv
dt
(1)
3–26
Separating variables and integrating we get
∫
vf
0
∫
t
dv = a t dt
0
vf = a t t
→
t=
v f 50.97 m / s
=
= 10.2 s
at
5 m / s2
3.3.3 Radial and Transverse Coordinates
Another coordinate system that is often convenient to use in solving problems is
radial and transverse coordinates, also known as polar coordinates. This coordinate
system is used when the most convenient way to describe a system is in terms of r
and θ, for example, when tracking an airplane with a radar tracking station as
shown in Figure 3.6 where
Where radial and transverse
coordinates fit in the kinematics
concept map
eˆ r
eˆ θ
eˆ r = a unit vector in the radial direction
eˆ θ = a unit vector in the transverse direction, that is, in the direction you would go
if you kept r constant and increased θ.
In this coordinate system we can write the position vector as
r
r = reˆ r
r
θ
Figure 3.6 - Plane tracked by
radar.
(3.16)
We can differentiate this to get the velocity and the acceleration. Again, I will
initially skip the derivation and just give the final results. I will include the
derivation after I give you the bottom line. The velocity in radial and transverse
coordinates is
v
r
v = r&eˆ r + rθ& eˆ θ = v r eˆ r + v θ eˆ θ
(3.17)
where
r
v θ = rθ& eˆ θ
r
v r = r&eˆ r
θ
r
O
v r = r& = the radial component of the velocity
v = rθ& = the transverse component of the velocity
θ
Figure 3.7 - Velocity vector
broken into radial and transverse
components
r
v = v 2r + v θ2 = speed
All we are doing is representing the velocity vector in terms of its components in
the radial and transverse directions as shown in Figure 3.7. If we take the
derivative of Eq. 3.17, we get the acceleration as shown in Eq. 3.18.
(
) (
)
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆ θ = a r eˆ r + a θ eˆ θ
where
a r = &r& − rθ& 2 = the radial component of the acceleration
a = r&θ& + 2r&θ& = the transverse component of the acceleration
θ
r
a = a 2r + a θ2 = the magnitude of the acceleration
(3.18)
3–27
a
r
a θ = r&θ& + 2r&θ&
r
a r = &r& − rθ& 2
r
O
The radial and transverse components of the acceleration are shown in Figure 3.8.
It is important to note that ar is not the time derivative of vr and aθ is not the time
derivative of vθ. When we were dealing with Cartesian coordinates, we could just
integrate ax to get vx (like we did for projectile motion problems), but that is no
longer the case for normal and tangential coordinates or radial and transverse
coordinates. This will become clear as we look at the derivation.
Warning! Derivation of velocity and acceleration in radial and transverse
coordinates.
θ
Figure 3.8 - Acceleration vector
broken into radial and transverse
components
r
If we take the derivative of the position vector r = reˆ r in radial and transverse
coordinates we get
r
r d r d(reˆ r )
v=
=
dt
dt
(3.19)
deˆ r
= r&eˆ r + r
dt
so, just as in the derivation for normal and tangential coordinates, we need the
derivative of a unit vector. Once again we will use the chain rule, that is,
deˆ r deˆ r dθ
=
dt
dθ dt
(3.20)
The derivative of the radial unit vector with respect to the angle θ is found in the
same way we found the derivative of the tangential unit vector with respect to θ in
the previous section. We find
deˆ r
= eˆ θ
(3.21)
dθ
and similarly for the derivative of the unit vector in the transverse direction (which
we will need later) we find
deˆ θ
= −eˆ r
(3.22)
dθ
unit circle
∆eˆ θ
∆θ eˆ θ
eˆ ′θ
eˆ ′r
∆θ
eˆ r
Looking at Figure 3.9 it is clear that the direction of ∆eˆ θ is in the negative eˆ r
∆eˆ r
Figure 3.9 - Illustration of
the change of the unit vectors
with θ.
direction. Substituting Eq. 3.21 into 3.20 we get
deˆ r &
= θeˆ θ
dt
(3.23)
Substituting Eq. 3.23 into Eq. 3.19 gives
r
v = r&eˆ r + rθ& eˆ θ
To find the acceleration we simply differentiate the velocity as shown in Eq. 3.24.
r
deˆ
deˆ
v = (&r&eˆ r + r& r ) + (r&θ& eˆ θ + r&θ&eˆ θ + rθ& θ )
dt
dt
(3.24)
3–28
We already have
deˆ θ
deˆ r
but we need
. Yes, you guessed it, we need to use the
dt
dt
chain rule again.
deˆ θ deˆ θ dθ
=
dt
dθ dt
(3.25)
Substituting Eq. 3.22 into Eq. 3.25 gives
deˆ θ
= −θ& eˆ r
dt
(3.26)
Now, if we substitute Eqs. 3.23 and 3.26 into Eq. 3.24 and collect terms we have
the acceleration of a point described in radial and transverse coordinates.
(
) (
)
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆ θ = a r eˆ r + a θ eˆ θ
End of Derivation
Example 3/14
P
A crane has a retractable boom as shown. The boom is
being retracted at a constant rate of 0.5 m/s while the crane
is being raised at 0.1 rad/s. Calculate the acceleration and
velocity of point P at the end of the boom at the instant shown.
10 m
θ=20°
Strategy: Since we are not given any forces or masses or told what is causing the crane to move, it looks like this is a pure kinematics
problem. The most natural way to describe the position of point P is by using polar coordinates.
The velocity and acceleration of a point in polar coordinates are
r
v = r&eˆ r + rθ& eˆ θ
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆ θ
(
) (
)
Let’s write what we know from the problem statement in terms of r and θ.
r = 10 m
r& = - 0.5 m/s = constant, &r& = 0
θ = 20o
θ& = 0.1 rad/s = constant, &θ& = 0
So, what we have here is a plug and chug problem.
r
v = (−0.5m / s)eˆ r + (10m)(0.1rad / s)eˆ θ
= −0.5eˆ r + 1eˆ θ m/s
(
)
r
a = 0 − (10m)(0.1rad/s) 2 eˆ r + ((10m)(0) + 2(−.5m/s)(0.1rad/s) )eˆ θ
= −0.1eˆ r − 0.1eˆ θ m/s
2
3–29
We have the velocity and acceleration in terms of radial and transverse unit vectors, but what if we want the magnitude and direction of
these? Let’s start by drawing a picture.
eˆ θ
y
v
eˆ r
ax
1
20°
eˆ θ
vy
x
eˆ r
20°
-0.1
20°
vx
-0.5
-0.1
ay
a
20°
From these figures we can easily determine the x and y components of the velocity and acceleration.
v x = −0.5 cos(20°) − 1 sin (20°) = −0.812 m/s
r
→ v = −0.812ˆi + 0.769ˆj m/s
v y = −0.5 sin (20°) + 1 cos(20°) = 0.769 m/s
a x = −0.1 cos(20°) + 0.1 sin (20°) = −0.0598 m/s
r
→ a = −0.0598ˆi − 0.128ˆj m/s
a y = −0.1 sin (20°) − 0.1 cos(20°) = −0.128 m/s
What if we wanted the magnitude and direction of the velocity and acceleration? The easiest way to determine these is to use the figures
shown above and the x and y components (or for the magnitudes we can just use the r and θ components) that have already been
determined.
r
r
v = (−0.812) 2 + (0.769) 2 = (−.5) 2 + (1) 2 = 1.12
→ v = 1.12 m/s 43.4 o
r
−1
o
angle of v = tan (0.769 / 0.812) = 43.4
r
r
a = (−0.0598) 2 + (−0.128) 2 = (−0.1) 2 + (−0.1) 2 = 0.14
→ a = 0.14 m/s 2 65.0 o
r
o
−1
angle of a = tan (0.128 / 0.0598) = 65.0
One more what-if and then I’ll let this problem go. What if I asked you to find the radius of curvature? The only equation we have with
the radius of curvature in it is the normal acceleration. That is,
an =
v2
v2
→ ρ =
ρ
an
We know the speed is 1.12 m/s so all we need is the normal component of the acceleration. How do we determine this? So far we know
the total magnitude and direction of the total acceleration, the x and y components of the total acceleration and the radial and transverse
components of the total acceleration, but unfortunately we don’t know the normal component of acceleration. Do we know the normal
direction? We know it is perpendicular to the tangential direction. Do we know the tangential direction? Yes! It is in the same
direction as the velocity vector! So, we have two choices at this point: 1) draw another picture of the acceleration with the normal and
tangential unit vectors labeled and then resolve the acceleration into normal and tangential coordinates, or 2) use some of the math
you’ve learned that you never thought you would use again. Let’s use the math. We know the dot product between a unit vector in the
tangential direction and the acceleration will give you the component of the acceleration in the tangential direction.
Tangential unit vector:
Take dot product:
r
v − 0.812ˆi + 0.769ˆj
eˆ t = r =
= −0.725ˆi + 0.687ˆj
v
1.12
r
r
a t = a ⋅ eˆ t = (−0.0598ˆi − 0.128ˆj) ⋅ (−0.725ˆi + 0.687ˆj)
= 0.0434 - 0.079 = -0.0446 m/s 2
3–30
The normal acceleration is therefore
a n = a 2 − a 2t = (0.14) 2 − (−.0446) 2
= 0.133 m/s 2
Let’s check this with the first approach we discussed, that is, draw a picture. From this
picture we see that β = 65° - 46.6° = 18.4° so
eˆ t
43.4°
2
an = a cos(18.4°) = 0.133 m/s
46.6° eˆ n
β
which is the same result we got using the dot product. Therefore, we can find the radius of
curvature at this instant:
65°
a = 0.14 m/s2
v 2 (1.12m / s) 2
=
a n 0.133m / s 2
= 9.45 m
ρ=
Example 3/15
At the bottom of a loop in the vertical (r-θ) plane at an altitude of
600 m, the airplane P has a horizontal velocity of 150 m/s and is speeding
up at a rate of 25 ft/s2. The radius of curvature of the loop is 1200 m.
The plane is being tracked by radar at O.
a) What is the force the pilot experiences at the instant shown?
Express your answer in terms of his mass, m.
150 m/s
r
600 m
θ
800 m
b) What are the recorded values of r&, &r&, θ& and &θ& for this instant?
Strategy: Since we want to find the force the pilot experiences at this instant, we should use LM rate, and since we are traveling in a
curved path we should either use normal and tangential coordinates or radial and transverse coordinates. For part b) we should use
radial and transverse, but for part a) we might as well use normal and tangential.
Summary of knowns: ρ = 600 m, v = 150 m/s and at = 25 ft/s2. We can also determine r and θ:
r = 800 2 + 600 2 = 1000m
θ = tan −1 (600 / 800) = 36.87o
Let’s pick the pilot as our system and draw the FBD and KD.
System: Pilot
LM n-direction (+↑ )
r
dPn
=
dt
KD
∑F
n
→
2
mp
v
= N − m pg
ρ
mpa n = m p
v2
ρ
FBD
eˆ n
(1)
mat
eˆ t
F
LM t-direction (+ →)
r
dPt
=
dt
∑F
t
→
mpa t = F
(2)
N
mpg
3–31
Solving these we get:
N = mp
(150m / s) 2
v2
+ m pg = m p
+ 9.81 = 47.3m p ↑
600m
ρ
F = 25mp→
We have solved for the x and y components of the force on the pilot. If we want the magnitude of the total force, we just need to take
the square root of the sum of the squares.
Ftotal = (25m p ) 2 + (47.3m p ) 2
= 53.5m p (which is 53.5/9.81 = 5.45g' s)
Let’s now work on part b). We want to find r&, &r&, θ& and &θ& , so let’s write the velocity and acceleration equations in terms of radial and
transverse components.
r
v = r&eˆ r + rθ& eˆ θ = v r eˆ r + v θ eˆ θ
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆ θ = a r eˆ r + a θ eˆ θ
(
) (
)
These vector equations result in 4 scalar equations
v r = r&
(1)
v θ = rθ&
(2)
a r = &r& − rθ& 2
(3)
a θ = r&θ& + 2r&θ&
(4)
We have 4 equations and 8 unknowns (vr, vθ, ar, aθ, r&, &r&, θ& , &θ& ). Where do we get more equations? We know the velocity and
acceleration, so we should be able to get the radial and transverse components of these.
vr = v cosθ
(5)
vθ = - v sinθ
(6)
eˆ r
eˆ θ
vr
θ
v = 150m/s
vθ
Similarly we can resolve the two components of acceleration into radial and transverse components.
ar = at cosθ + an sinθ
(7)
aθ = ancosθ – at sinθ
(8)
an =
eˆ θ
So we have 8 equations and 8 unknowns and can solve for vr, vθ, ar, aθ, r&, &r&, θ& , &θ& .
θ
eˆ r
θ
v2
= 36.5 m/s 2
ρ
at = 25m/s2
3–32
Example 3/16
A centrifugal pump with smooth radial vanes rotates about its
vertical axis with a constant angular velocity, ω = θ& . Find the
magnitude of the force exerted by a vane on a particle of mass m
as it moves out along the vane. The particle is introduced at r = r0
with no angular velocity. Assume there is no shear force between
the particle and the vane.
r0
r
Particle
Strategy: Since we want to find the force exerted on the particle, let’s use LM rate. The particle will be moving along a curved path, so
we should use normal and tangential or radial and transverse coordinates. Let’s try radial and transverse first.
LM r-direction (+
r
dPr
=
dt
KD
∑F
r
∑F
θ
ma r = m(&r& − rθ& 2 ) = 0
→
LM θ-direction (+
r
dPθ
=
dt
)
→
)
(1)
maθ
System = Particle
(top view)
mar
FBD
eˆ θ eˆ r
0
ma θ = m(r&θ& + 2r&θ& ) = N
(2)
N
From Eq. 2 we find N = 2mr&θ& , so all we need is r& since we are given ω = θ& . How do we get r& ? From Eq. 1 we have &r&, so we
should be able to integrate this to get r& .
&r& =
dr&
= rθ& 2 = rω 2
dt
(3)
To integrate this, we need a dr, so let’s use the chain rule
&r& =
dr& dr
dr&
= rθ& 2
→ r& = rω 2
dt dr
dr
Separate variables and integrate
r&
∫
r
∫
r&dr& = rω 2 dr
r0
0
1 2
r&
2
r&
0
1 2 1 2 2 2
r& = ω (r − ro )
2
2
=
1 2 2
ω r
2
r
ro
→ r& = ω r 2 − ro2
Substituting into Eq. 2 we get the normal force
N = 2mω2 r 2 − ro2
What if (you know we have to have a what if) you had been asked to find the normal force as a function of time? We can still use Eq. 3
except we cannot separate variables and integrate. What we have is a differential equation.
3–33
d2r
dt
2
− rω 2 = 0
If you have had differential equations, you know this is easy to solve. If not, we can always use Dsolve in Maple as shown below.
So if we differentiate this to get r& , we get
r& =
dr
= ro ω sinh( ωt )
dt
which when substituted into Eq. 2 gives
N = 2mro ω 2 sinh(ωt )
Example 3/17
To simulate “weightlessness” in its cabin, a jet transport traveling
at 800 km/hr (222.2 m/s) moves on a sustained vertical curve as shown.
This means that the plane remains approximately parallel to the ground
but its center follows the curve shown. This maneuver takes place at a
mean altitude of 8 km where the gravity may be taken as 9.79 m/s2.
Determine:
a) the radius of curvature, ρ
β&
ρ
β&
b) the rate β& in degrees per second at which the pilot should
drop his longitudinal line of sight to cause the desired condition.
Strategy: We want to find the radius of curvature, which leads us to think of normal and tangential coordinates. Since we want to
experience “weightlessness”, that is, the normal force between a passenger and the plane is zero, we should use LM rate.
Let’s start with a FBD and KD. Since we are traveling in a circle, we will put the normal acceleration on the KD.
FBD
KD
mg
System: Passenger
m
LM n-direction (+ ↓)
which we can solve for ρ
r
dPn
=
dt
∑F
n
v2
ρ
N=0
→
m
v2
= mg
ρ
3–34
ρ=
v 2 (222.2 m / s) 2
=
= 5043 m
g
9.79 m / s 2
For part b) we want the rate of change of the angle, β. Let’s use polar coordinates for the velocity. The general equation is
r
v = r&eˆ r + rθ& eˆθ
0 (since we are traveling in a circle)
so we get (for this problem θ = β)
r
v = rβ& eˆ θ
The magnitude of the velocity is therefore v = rβ& so solving for β& we get
v 222.2 m/s
β& = =
= 0.044 rad / s = 2.52 o / s
r
5043 m
3.3.4 Summary of Different Coordinate Systems
In summary, for particles we have looked at three ways of describing the velocity
and acceleration vectors: Cartesian coordinates, normal and tangential coordinates
and radial and transverse coordinates. The coordinate system we choose depends
on the type of problem and the type of information given. A summary of how an
acceleration vector can be broken down into these three different coordinate
systems is shown in Figure 3.10 and a summary of all of the equations is shown in
Table 3.1.
Particle
ax
at
ar
aθ
r
an
y
θ
ay
a
(total acceleration)
Path of
particle
x
Figure 3.10 - Illustration of how an acceleration vector
can be resolved into Cartesian, normal-tangential or
radial-transverse components.
3–35
Table 3.1 Summary of equations for representing position, velocity and acceleration in various coordinate
systems
Coordinate System
Position
r
r = xˆi + yˆj
Velocity
r
v = x& ˆi + y&ˆj
Acceleration
r
a = &x&ˆi + &y&ˆj
Cartesian
Normal and Tangential
N/A
r
v = veˆ t
r
v2
a = v& eˆ t +
eˆ n
ρ
Radial and Transverse
r
r = reˆ r
r
v = r&eˆ r + rθ& eˆ θ
r
a = &r& − rθ& 2 eˆ r + r&θ& + 2r&θ& eˆ θ = a r eˆ r + a θ eˆ θ
(
) (
)
3.4 Impact
In ES201 you have already dealt with plastic impact, that is, when the two objects
stick together. In this chapter we will be examining cases where objects bounce off
of each other. Before we do that, let’s define some terms. The “line of impact” is a
line along the common normal to the surfaces in contact as shown in Figure 3.11.
The “plane of contact” is perpendicular to the line of impact.
vA
line of impact
t
A
plane of contact
vB
B
n
Figure 3.11 - Generic illustration of an impact showing
the definition of the line of impact (along the normal) and
the plane of contact.
In most Dynamics books, impacts are usually broken down into a number of types
depending on the location of the mass center with respect to the line of impact and
the alignment of the velocity vectors with respect to the line of impact. These
categories are shown below.
Central Impact: Both mass
centers are located on the line
of impact (always true for
particles).
3–36
Eccentric Impact: Both mass
centers are not located on the line
of impact.
Direct Impact: Both
velocities, vA and vB,
lie along the line of
impact.
Oblique Impact: Both
velocities, vA and vB,
do not lie along the
line of impact.
Impacts can therefore be categorized as “direct-central” or “oblique-central” or
“direct-eccentric” or “oblique-eccentric”.
These delineations are really
unnecessary when solving a problem, however, since all you need is the finite time
form of conservation of linear (and possibly angular) momentum and something
called the “coefficient of restitution.”
The coefficient of restitution is an
experimentally determined quantity and is assumed to be a constant for a given
combination of materials. The most general equation for the coefficient of
restitution in terms of the velocities before and after impact is shown in Eq. 3.27.
v ′PB n − v ′PA n
e = −
v PB − v PA
n
n
or
(
) (
v ′PB n − v ′PA n = -e v PB n − v PA n = e v PA n − v PB n
)
(3.27)
where
e
= the coefficient of restitution (0 ≤ e ≤ 1)
3–37
n
B
after the impact
′
=
the
velocity of the point of contact on object B in the normal direction
v PB n
after the impact
v PA n = the velocity of the point of contact on object A in the normal direction
P
A
v′PA n = the velocity of the point of contact on object A in the normal direction
t
v PB n
Figure 3.12 - The coefficient of restitution
uses the normal component of velocity at
the point of contact.
before the impact
= the velocity of the point of contact on object B in the normal direction
before the impact
This equation is valid for either rigid bodies (discussed in the next chapter) or for
particles. One important thing to note is that the coefficient of restitution uses the
normal component of the velocity of the point of contact as shown in Figure 3.12.
For particles we usually simplify this equation to
(
v′B n − v′A n = e v A n − v B n
)
(3.28)
Eq. 3.28 is what we will be using in this chapter. There are two special cases that
are given names.
• e = 0 is called a plastic impact
• e = 1 is called an elastic impact. This is the only case in which mechanical
energy is conserved.
Note: The most common mistake
when applying the coefficient of
restitution equation is getting the
signs wrong on the various terms.
The most common mistakes made when applying these equations are sign errors.
Students draw impulse-momentum diagrams, therefore defining the directions for
vA and vB and then they are not consistent when they use the coefficient of
restitution equation, so be careful!
Warning: Derivation of where the coefficient of restitution comes from (sort
of).
vA > vB
Before
Impact
A
B
vA
vB
Maximum
Deformation
During Impact
A
B
v AB
v ′A < v ′B
After
Impact
A
v ′A
B
v ′B
Figure 3.13 - Details of a
direct central impact.
In the next few paragraphs I will explain the traditional way of showing where the
coefficient of restitution comes from, but the fact of the matter is that you should
just consider Eq. 3.27 or Eq. 3.28 to be constitutive relationships where e must be
determined experimentally. Let’s look at a direct central impact in more detail.
Figure 3.13 shows a typical impact assuming A and B are initially traveling in the
same direction both before and after the impact. This will obviously affect the final
equation we will derive. If one of the objects were traveling in the opposite
direction, we would need to be sure to make that velocity a negative quantity in our
final equation. Before the impact, A must have a greater velocity than B (or else
there won’t be an impact). When the two objects hit, they will deform until both A
and B have the same velocity, vAB (this will be the point of maximum deformation
of the objects). We’ll call this the deformation phase of the impact. The objects
will then rebound until they are no longer touching (we’ll call this the restoration
part of the impact) and object B will now be traveling faster than object A. We will
use a prime to denote the velocities after the impact.
3–38
If we draw impulse-momentum diagrams for A during the deformation and
restoration phases of the impact, we get the figures shown in Figure 3.14. We will
define t1 to be the time it takes to reach the maximum deformation and t2 the time
until A and B finally separate. Applying the finite time form of conservation of
linear momentum during these two parts of the impact we get
m A v AB − m A v A = −
Particle A
(deformation)
t1
0
Pdt
and
m A v AB
mAvA
∫
t1
0
m A v ′A − m A v AB = −
Pdt
m A v ′A
m A v AB
∫
t2
t1
∫
t2
t1
Rdt
We will define the coefficient of restitution to be equal to the restoration impulse
divided by the deformation impulse, that is,
t2
Particle A
(restoration)
∫
∫
e=
∫
t1
Rdt
t1
0
Rdt
=
Pdt
m A v ′A − m A v AB v ′A − v AB
=
m A v AB − m A v A v AB − v A
We can do the same thing for particle B resulting in
Figure 3.14 - Impulse-momentum
diagrams for object A
t2
∫
e=
∫
t1
t1
0
Rdt
=
Pdt
m B v ′B − m B v AB v ′B − v AB
=
m B v AB − m B v B v AB − v B
Eliminating vAB we get
e=−
v ′B − v ′A
vB − vA
This equation is only valid for direct central impact, but if we know the velocities
before and after the impact, we can determine the coefficient of restitution, which is
the way it is determined experimentally. The main reason for showing this to you
is to help you understand how this generalizes to other types of impact problems.
In this discussion we used the ratio of the deformation and restoration impulses to
define the coefficient of restitution. For oblique impacts, only the normal
component of velocity will affect these impulses, which is why our equation uses
the normal components of velocity as shown below.
v ′B − v ′A n
e=− n
v Bn − v A n
This is Eq. 3.28 which was given before the derivation. Finally, to get Eq. 3.27,
our most general form for the coefficient of restitution, we just need to realize that
for a rigid body, since different points on the object will have different velocities,
we simply need to use the normal component of the velocity of the point of contact,
we’ll call it point P, between the two objects.
v ′PBn − v ′PA n
e=−
v PBn − v PA n
End of derivation
3–39
3.4.1 Comments on the coefficient of restitution
It turns out the coefficient of restitution is really an idealization that is not that
realistic except in special cases. In general, it will depend on the sizes, shapes and
material properties of the two objects colliding, in addition to the velocity of the
impact. Impacts and other types of contact, such as rolling and sliding, are very
difficult to model in practice. Some rigid body dynamics codes such as Working
Model use the coefficient of restitution to model impacts, but the user should
recognize the difficulty in determining this parameter and that it is generally not a
constant. So, is there anything else we can do? Yes, using a coefficient of
restitution is not the only way to model an impact. Another common way of
modeling an inelastic impact is to put a spring and damper between the two objects
that are hitting each other. The problem with this method is determining the
stiffness and damping values to be used to model the impact, because again, in
general they will not be constants. In this book we will exclusively use the
coefficient of restitution to model inelastic impacts.
Example 3/18
For the two object shown, determine their final velocities
after they collide. Assume the coefficient of restitution
is 0.5 and the mass of the objects A and B are 1 lbm
and 0.8 lbm respectively.
40°
A
vA= 1 ft/s
B
25°
vB= 1 ft/s
Strategy: We have an impact problem which immediately makes us think of LM finite time. We will also need to use the coefficient of
restitution equation.
Before we start with our principle, I like to get some of the preliminary calculations out of the way. Let’s determine the mass of A and
B in a more useful unit, i.e. slugs. The easiest way to do this is to use the conversion factor between lbm and slugs, that is, 32.174 lbm =
1 slug, so mA = 0.0311 slug = .0311 lbf-s2/ft, and mB = 0.0249 slugs = 0.0249 lbf-s2/ft.
To use LM finite time, let’s draw our impulse momentum diagrams and label our n and t directions. For most impact problems it is
easiest to draw this diagram using both objects as our system.
n
40°
m A v ′A n
m A v ′A t
t
m B v′B t
B
Momentum after
time interval
n
t
40°
A
m B v ′Bn
n
mAvA
t
A
A
B
F∆t
25°
mBvB
Momentum before
time interval
B
F∆t
Impulses during
time interval
I’d like to make a few observations on these figures before we use them. The time interval we are considering is immediately before the
impact to immediately after the impact. Since we don’t know the directions of A or B after the impact I have just put general n and t
components. In the figure on the far right, i.e. the “Impulses during” figure, I’ve included the internal force between the two objects
3–40
(equal and opposite on each object), so we can use these same figures for any of the following systems: A and B together, A alone or B
alone. We only have two objects, so remember we only get two independent systems.
System A+B
LM n-direction (+
)
∆Psysn =
LM t-direction (+
∑ F ∆t
n
→
(m A v′A n + m B v′B n ) − (−m A v A cos(40°) + m B v B cos(25°)) = 0
(1)
(m A v′A t + m Bv′B t ) − (m A v A sin (40°) − m B v B sin (25°)) = 0
(2)
)
∆Psys t =
∑ F ∆t
t
→
So, we have 2 equations and 4 unknowns ( v ′A t , v ′A n , v ′B t , v ′Bn ) . We need two more equations. Let’s pick a new system, particle A,
and look in the t-direction.
System A
LM t-direction (+
)
∆Psys t =
∑ F ∆t
t
→
(m A v′A t ) − (m A v A sin (40°)) = 0
(3)
Should we also look at the n-direction? We could, but we really don’t care what the internal impulse F∆t is, so looking in the n-direction
doesn’t help (we get another equation, but we also get another unknown). Can we look at B by itself? NO! We only get two systems.
Note that if we were going to solve this problem by hand (and were therefore concerned about the amount of algebra), instead of Eq. 2
we could have looked at B in the t-direction to obtain an alternative equation to Eq. 2 where we looked at A and B together. We still
need another equation. We don’t have any more systems, but we still have the coefficient of restitution equation. We’ll write the
equation in general terms first and then substitute in for our problem.
(
v′B n − v′A n = e v A n − v B n
)
Substituting in we get
v′B n − v′A n = e((− v A cos(40°)) − ( v B cos(25°)) )
So we now have 4 equations and 4 unknowns and can solve in Maple.
(4)
3–41
We now have the n and t components of the final velocities of A and B. If we want the x and y components (or a magnitude and
direction) we simply need to draw a picture and find the components in the x and y direction. I’ll do this for one of them, A, to illustrate
t
(although we’ve already done it several times in this chapter so far, so feel free to skip this if you’d like).
n
v A x = 0.643 sin (40°) − 0.488 cos(40°) = 0.039 ft/s
v′A n = 0.488 ft / s
v A y = 0.643 cos(40°) + 0.488 sin (40°) = 0.806 ft/s
A
v′A t = 0.643 ft / s
40°
or
r
v A = (0.039 ˆi + 0.806ˆj)ft/s
= 0.81 ft/s ∠87.2 o
The exact same approach is valid for B.
Example 3/19
A 10-kg ball moving horizontally at 12 m/s strikes a 10-kg block. The coefficient of restitution of the impact is 0.4 and the coefficient
of kinetic friction between the block and the inclined surface is 0.5. Determine the necessary equations to solve for the distance the
block will slide before stopping.
25°
Strategy: We have an impact, so we will need to use LM finite and the coefficient of restitution. The time interval will be immediately
before the impact to immediately after the impact. After the impact we want to determine how far the block will slide up the incline.
We can either use LM rate to find the acceleration and then integrate or we can use conservation of energy. Let’s use the latter.
Impulse-momentum diagrams
m A v′A t
n
25°
mAvA
m B v′B n
m A v′A n
n
n
25°
t
F∆t
25°
F∆t
t
t
R∆t
Momentum after
time interval
Momentum before
time interval
Impulses during
time interval
Since we do not care about F∆t or R∆t, let’s just use conservation of LM finite in the n-direction.
System A+B
LM n-direction (+
)
∆Psysn =
∑ F ∆t
n
→
(m A v′A n + m B v′Bn ) − (m A v A cos(25°)) = 0
(1)
3–42
So, we have 1 equation and 2 unknowns ( v′A n , v′B n ). We need one more equation that involves the n components, which is of course,
the coefficient of restitution equation.
(
v ′Bn − v ′A n = e v A n − v Bn
)
(2)
= e(( v A cos(25°)) − (0) )
We now have 2 equations and 2 unknowns and can solve for the normal components of the velocities after the impact. We get
v′A n = 5.24 m/s
v′Bn = 5.64 m/s
To solve the second part of the problem, we will use conservation of energy (finite time) with block B as the system.
E sys2 − E sys1 = W
1
m B ( v′B ) 2
2
= m Bgd sin 25
E sys1 = E k1 =
E sys 2 = E g 2
2
d
where
datum
1
25°
W = work due to friction. To find the friction force we can use LM rate
and draw a FBD and KD. We will find that the normal force, N, is
N = mgcos(25°)
and therefore the sliding friction is
F = µkN = µk mgcos(25°)
The work of friction is
W = -µkNd = -µkmgdcos(25°)
Substituting into conservation of energy we get
m Bgd sin( 25°) −
1
m B ( v′B ) 2 = -µ k m Bgd cos(25°)
2
We can now solve for d since it is the only unknown in this equation.
The final answer is therefore d = 1.85 m.
3–43
Example 3/20
The university’s tennis coach has asked your help in developing
a technique for sorting tennis balls according to their coefficient of
restitution. The general concept is shown in the figure where h = 6 ft.
You have been asked to determine
a) the optimal angle, θ, to maximize the distance x given the
coefficent of restitution, e = 0.5.
b) the minimum distance, b, assuming we want tennis balls to enter the
bin on the right for 0.5 < e < 1.0.
c) plot the angle as a function of e.
h
x
b
θ
reject bin
accept bin
Strategy: We have three stages of motion in this problem. 1) tennis ball falls (conservation of energy), 2) impact (LM finite) and 3)
projectile motion.
Tennis ball falls (conservation of energy). System = tennis ball.
E sys2 − E sys1 = W
where W = 0, E sys1 = E g1 = mgh (datum is at the bottom), E sys 2 = E k 2 =
mgh −
1
mv 2 = 0
2
→
1
mv2 so substituting we get
2
v = 2gh
(1)
For the impact, let’s use LM finite, so we need to draw our impulse momentum diagrams. Our system will be the tennis ball (note: you
cannot put the ground in your system!).
θ n
mv θ
mv′n
n
mv′t
t
t
Momentum after
time interval
LM t-direction (+
θ
F∆t
Momentum before
time interval
n
t
Impulses during
time interval
)
∆Psys t =
∑ F ∆t
t
→ (mv ′t ) − (mv sin θ) = 0
so
v′t = v sin θ
(2)
3–44
Applying LM finite in the n-direction really doesn’t help (since we don’t care what F∆t is), so let’s use the coefficient of restitution
equation. The general equation is
(
v ′Bn − v ′A n = e v A n − v Bn
)
Substituting in for our problem (A = ball, B = ground)
0 − v′n = e(v cos θ − 0 )
→ v′n = −ev cos θ
(3)
The negative sign means that the ball travels in the negative n-direction. The next step of the problem is to do the projectile motion part.
Let’s find the x and y components of the ball’s velocity after the impact.
v o x = ev cos θ sin θ + v sin θ cos θ
(4)
= (e + 1) v sin θ cos θ
vo y = ev cos 2 θ − v sin 2 θ
θ
v′n = ev cos θ
(5)
v′t = v sin θ
For projectile motion we know that the acceleration in the x-direction is zero and in the ydirection is –g. Integrating these we get the standard projectile motion equations:
x = vo x t
(6)
1
y = yo + vo y t − gt 2
2
(7)
We really should be counting knowns and unknowns! If we assume y = yo, then our unknowns are v, θ, v′n , v′t , t , v o x , v o y and x, so it
looks like we have 8 unknowns and 7 equations. We already substituted into Eq. 4 and 5, so if we consider our unknowns to be
v, θ, t , vo x , vo y , x and our equations to be 1,4,5,6,7 we will have six unknowns and 5 equations. What we can do is to solve for x in
terms of θ and then determine the value of θ to maximize x by taking a derivative and setting it equal to zero. We can go to Maple at
this point or do a little simplification by hand first (which is what I like to do). Using y = yo we can use Eq. 7 to solve for t
2vo y
1
→ t =
0 = 0 + vo y t − gt 2
2
g
which when substituted into Eq. 6 gives
x=
2vo y vo x
g
So let’s put Eq. 4, 5 and 8 into Maple and solve for x as a function of θ.
(8)
3–45
Let’s plot the distance, x, as a function of θ to see if we can make sense of these two solutions.
So clearly, θ = 18.7° represents a maximum and θ = 64.5° represents a minimum. From Maple we can easily get the distance traveled
using this angle for e = 0.5 and e = 1.0 (to determine the minimum distance b.)
So, for e = 0.5 the distance x = 3.78 ft and for e = 1 the distance x = 11.58 ft, so the distance b = 11.58 - 3.78 = 7.8 ft. These numbers
were calculated assuming the ball was dropped from a height of six feet.
Let’s now find the general solution for θ as a function of e and plot it. The Maple solution is shown below.
3–46
Let’s look at one last problem that uses a lot of principles.
Example 3/21
A game has been designed as shown below. A 1 lb block,
block A, is pushed up against a spring compressing it a
distance, x. The block is then released from rest and
slides down the 20° incline until it strikes ball B. Ball
B weighs 0.5 lb and the coefficient of restitution between
A and B is 0.7. Ball B is suspended by an inextensible rope.
Determine how far the spring needs to be initially compressed
for B to swing around and land in the basket.
The following parameters are known:
k = 100 lb/in, L = 10”, d = 9”, µk = 0.3, xB = 3”, yB = 5”.
xB
yB
k
L
A
µk
`
20°
B
x
d
I’m going to put the strategy on the next page so the text goes better with the figure. Before we start we should spend a few seconds
talking about units. Since we are using English units, we are going to need to calculate the masses of A and B in slugs. Remember,
1 slug = 1 lbf-ft/s2, that is, there is a “ft” in a slug. So, to be consistent, we need to either calculate the mass in lbf-s2/in, or we need to
convert all the quantities given in inches to feet. Let’s do the mass.
mA =
mB =
1 lbf
(32.2 ft/s 2 )(12 in/ft)
0.5 lbf
2
(32.2 ft/s )(12 in/ft)
= 0.00259 lbf - s 2 /in
= 0.00129 lbf - s 2 /in
3–47
Strategy: A lot of things are going on in this problem, so let’s break the motion down into steps. I’ve redrawn the figure and
labeled the various stages of the problem.
Step 1: A slides down the incline.
Step 5 – Projectile
Strategy: Conservation of energy.
motion
Step 2: A hits B.
Step 4 – Rope
Strategy: Finite time form of conservation of linear momentum and
xB
goes slack
the coefficient of restitution equation.
Step 3: B swings up until the rope goes slack.
Strategy: Conservation of energy.
yB
Step 4: The rope goes slack.
Strategy: Rate form of conservation of linear momentum
Tension equals zero.
Use normal and tangential coordinates.
Step 5: Projectile motion.
Step 1 - Sliding
Strategy: Use constant acceleration equations.
k
L
A
Step 3 – B swings
Let’s start solving the problem!
up until the rope
µk
goes slack
20°
B
x
d
Step 2 - Impact
Step 1 – Sliding
For the system we will pick A and the spring. We start by drawing the system
in the two positions and defining our datum at position 2 as shown.
k
Position 1
A
Conservation of Energy is
E sys2 − E sys1 = W
µk
(1)
20°
x
Datum
d
To determine the work, we need to draw a FBD as shown. The spring force
will not do any work because it will not travel through any distance (since we
cut it at the wall), and the normal force is perpendicular to the motion.
Therefore, the only force doing work is the friction force. Since the friction is constant, the work is
W = -µkN(x+d)
Position 2
Fs
(1a)
FBD
mAg
We can find the normal force using conservation of linear momentum in the y-direction.
µkN
y-direction (+ )
dPsys y
dt
=
∑F
y
→ 0 = N - m A gcos(20°)
→ N = m A gcos(20°)
Now let’s find the energy at positions 1 and 2.
Energy at position 1:
E sys1 = E k1 + E g1 + E s1
(1c)
where
E k1 = 0 (released from rest)
(1d)
(1b)
N
3–48
E g1 = m A g(x + d ) sin 20°
E s1 =
(1e)
1 2
kx
2
(1f)
Energy at Position 2:
E sys2 = E k 2 + E g 2 + E s 2
(1g)
where
E k2 =
1
m A v 2A
2
(1h)
E g 2 = 0 (datum)
(1i)
E s2 = 0
(1j)
Substituting Eqs. 1a-1j into Eq. 1 we get
1
1
m A v 2A − m A g(x + d ) sin 20° + kx 2 = −µ k (m A g cos 20°)(x + d )
2
2
(1)
We have 1 equation and 2 unknowns (x, vA).
Step 2: A hits B
For the impact we will use the finite time form of linear momentum. For the system we will pick A and B and start by drawing impulsemomentum diagrams.
m A v ′A
mAvA
20°
m B v ′B
-
=
20°
F∆t
R∆t
R∆t
x
n
LM x-direction (+
y
)
∆Psys x =
∑ F ∆t
x
→ (m A v ′A cos 20° + m B v ′B ) − (m A v A cos 20°) = 0
(2)
We are not interested in the impulse in the rope, so we won’t bother applying LM in the y-direction. We now have 2 equations and 4
unknowns ( v ′A , v ′B , v A , x ) . We still have the coefficient of restitution equation. The general equation is
(
v ′Bn − v ′A n = e v A n − v Bn
)
We will define the positive normal direction to be down the incline. Substituting in for our problem we get
v′B cos 20° − v′A = e(v A − 0 )
(3)
So now we have 3 equations and 4 unknowns. Let’s move on to step 3.
Step 3 – Ball B swings up
We are going to use conservation of energy, but we are not sure where the string will go slack, so we
will draw our second position at some unknown angle, α. Our system will be the ball and the string.
Position 3
α
Conservation of Energy is
E sys2 − E sys1 = W
L
datum
Position 2
3–49
There will be no work done, so the energy at positions 2 and 3 will be equal to each other, that is
E sys2 = E sys1
We only have kinetic and gravitational energy so we have
1
1
m B v 32 + m B g(L + L sin α) = m B v ′B2
2
2
(4)
Where we will define v3 as the velocity of ball B at the point the rope goes slack. We now have 4 equations and 6 unknowns
( v ′A , v ′B , v A , x , v 3 , α ) . At position 3 we know the tension must go to zero, so let’s move on to step 4.
Step 4 – Tension is zero
To apply the rate form of conservation of linear momentum we will draw a
FBD and KD as shown. The system is ball B.
m Ba t
KD
t
LM in n-direction
dPsysn
dt
=
∑F
n
FBD
→ m B
v 32
= m B g sin α
L
(5)
m Ba n = m B
v 32
L
T=0
α
n
mBg
We are not interested in the tangential acceleration, so we won’t apply linear momentum in the t-direction. We now have 5 equations
and 6 unknowns. Finally, onto step 5.
v3
Step 5 – Projectile motion
Let’s draw a picture so we can get a better handle on this part of the problem.
will define the origin of a coordinate system at point O.
α
xB
For projectile motion, the acceleration in the y-direction = -g and the
acceleration in the x-direction is zero. Therefore, we have
x-direction: x = x O + v o x t
1
y-direction: y = y O + v o y t − gt 2
2
L
y
Applying these to our specific problem we get
x B = L cos α − v 3 sin αt
(6)
1
y B = L sin α + v 3 cos αt − gt 2
2
(7)
O
We
yB
α
x
We now have 7 equations and 7 unknowns ( v ′A , v ′B , v A , x , v 3 , α, t ) and we are done! The Maple solution is shown below. Note:
When I first tried solving the equations, it did not work. This could have been because of the squared term or the alpha (Maple
sometimes has problems with trig function when you ask it to solve) so I had to use fsolve. When I first did this I got an answer that
didn’t make sense (I’ve left it in the printout for you to see) so I put intervals on the variables to solve. This enabled Maple to solve the
problem.
Define all the knowns and calculate the masses
> WA:=1: WB:=0.5: e:=0.7: th20:=20*Pi/180: k := 100:
g:=32.2: L:=10: d:=9: muk:=0.3: xB:=3: yB:=3:
mA:=WA/g/12;
mB:=WB/g/12;
mA := 0.002587991718
mB := 0.001293995859
Input the 7 equations we derived
> eq1:=1/2*mA*vA^2-(mA*g*(x+d)*sin(th20)+1/2*k*x^2)=-muk*mA*g*cos(th20)*(x+d);
eq2:=mA*vAp*cos(th20)+mB*vBp-(mA*vA*cos(th20))=0;
3–50
eq3:=vBp*cos(th20)-vAp=e*vA;
eq4:=1/2*mB*v3^2+mB*g*(L+L*sin(alpha))=1/2*mB*vBp^2;
eq5:=mB*v3^2/L=mB*g*sin(alpha);
eq6:=xB=L*cos(alpha)-v3*sin(alpha)*t;
eq7:=yB=L*sin(alpha)+v3*cos(alpha)*t-1/2*g*t^2;
π
π
eq1 := 0.001293995859vA2 − 0.9999999998 ( x + 9) sin − 50 x2 = −0.30000000000cos ( x + 9 )
9
9
π
π
eq2 := 0.002587991718vAp cos + 0.001293995859vBp − 0.002587991718vA cos = 0
9
9
π
eq3 := vBp cos − vAp = 0.7 vA
9
eq4 := 0.0006469979295v3 2 +4.9999999999 + 4.999999999 sin( α) = 0.0006469979295vBp 2
eq5 := 0.0001293995859v3 2 = 0.499999999 sin (α )
eq6 := 3 = 10 cos ( α ) − v3 sin( α ) t
eq7 := 5 = 10 sin( α ) + v3 cos ( α ) t − 16.10000000t2
Solve these equations
> fsolve({eq1,eq2,eq3,eq4,eq5,eq6,eq7},{alpha,v3,vA,vAp,vBp,x,t});
{ α = 2.294345296, t = 0.8263150445, v3 = -15.53468371, vA = 32.02094660, vAp = 12.34099917,
vBp = 36.98620275, x = 0.1600563018}
A negative v3 doesn't make sense, and an angle larger than 90 degrees is clearly wrong, so
lets put some limits on fsolve.
>fsolve({eq1,eq2,eq3,eq4,eq5,eq6,eq7},{alpha,v3,vA,vAp,vBp,x,t},{alpha=0..Pi/2,v3=0..1000,v
A=0..1000,vAp=0..1000,vBp=0..1000,x=0..1000,t=0..100});
{ α = 0.5818736778, t = 0.7323518638, v3 = 13.30293410, vA = 29.67533583, vAp = 11.43699153,
vBp = 34.27687511, x = 0.1478986597}
Let's figure out the angle in degrees
> evalf(0.5339*180/Pi);
33.33869522
We can tell by a quick look at the answers that these numbers seem reasonable. For example, the velocity of A after the impact is less
than it is before the impact and the angle is less than 90 degrees. So, our final answer for the required compression of the spring is:
x = 0.512 inches
3-51
Problems
Problem 3.1
A 2700-lb automobile starts from rest and travels a quarter of
a mile. Assume that the coefficient of static friction between
the tires and the pavement is 0.70, the automobile has frontwheel drive, the front wheels support 62% of the
automobile’s weight, and air resistance must be considered
where the aerodynamic drag D has a magnitude D = 0.012 v 2,
where D and v are expressed in pounds and ft/s, respectively.
(a) Determine the maximum theoretical speed. (b) Plot the
maximum speed as a function of the coefficient of static
friction over the domain 0.3 < µs < 0.9. Note: The word
“plot” means to use appropriate software and not a sloppy
hand sketch!
Problem 3.2
The velocities of commuter trains A and B are as shown.
The speed of each train is constant and B reaches the
crossing 10 min after A passed through the same crossing.
Determine a) the relative velocity of B with respect to A
and b) the distance between the fronts of the engines 3
min after A passed through the crossing.
66 km/h
A
Problem 3.4
The masses of blocks A, B, and C are mA = 4 kg, mB = 10
kg, and mC = 2 kg. Neglect the masses of the pulleys and
the effect of friction. Assuming the blocks are released
from rest, determine a) the acceleration of each block, b)
the tension in the cord and c) the distance block A will
travel in 2 seconds.
C
B
A
Problem 3.5
Block B has a mass of 10 kg and rests on the upper
surface of a 22-kg wedge, A, as shown. The system is
released from rest and friction is negligible. Determine a)
the acceleration of B, and b) the velocity of B relative to
A at t = 0.5 s.
A
B
B
B
25°
20°
48 km/h
A
30°
Problem 3.3
A conveyor belt A, which forms a 20° angle with the
horizontal, moves at a constant speed of vA = 4 ft/s and is
used to load an airplane. A worker tosses duffel bag B
with an initial velocity of (vB)0 = 2.5 ft/s at an angle of 30°
with the horizontal. Assume the bag does not rotate.
Determine the velocity of the bag relative to the belt as it
lands on the belt.
(vB)0
B
A
30°
A
vA
1.5 ft
20°
Problem 3.6
During a high-speed chase, a 2400-lb sports car traveling
at a speed of 100 mi/h just loses contact with the road as it
reaches the crest A of a hill. a) Determine the radius of
curvature ρ of the vertical profile of the road at A. b)
Using the value of ρ found in a part a), determine the
force exerted on a 160-lb driver by the seat of his 3100-lb
car as the car, traveling at a constant speed of 50 mi/h,
passes through A.
ρ
3-52
Problem 3.7
A small block slides at a speed v = 8 ft/s on a horizontal
surface at a height h = 3 ft above the ground. Determine
a) the angle θ at which it will leave the cylindrical surface
BCD and b) the distance x at which it will hit the ground.
Neglect friction and air resistance.
v
B
C
θ
h
D
E
x
Problem 3.8
A thin circular rod is supported in a vertical plane by a
bracket at A. Attached to the bracket and loosely wound
around the rod is a spring of constant k = 3 lb/ft and
undeformed length equal to the arc AB. An 8-oz collar is
unattached to the spring and can slide without friction
along the rod. The collar is released from rest when θ =
30°. Determine, a) the velocity of the collar as it passes
through point B, b) the force exerted by the rod on the
collar as it passes through B, and c) plot the velocity of the
collar as it passes through point B as a function of the
initial angle, θ, over 15° < θ < 45°.
Problem 3.9
The rotation of rod OA about O is defined by the relation
θ = π (4t2 - 8t), where θ and t are expressed in radians and
seconds, respectively. Collar B slides along the rod so
that its distance from O is r = 10 + 6 sin πt, where r and t
are expressed in inches and seconds, respectively. When t
= 1.2 s, determine: a) velocity of the collar in radial and
transverse components, b) acceleration of the collar in
radial and transverse components, c) plot the path of collar
B from t = 0 to t = 1.25 s using the following Maple
commands (you need to type this all on one line):
plot({[10+6*sin(Pi*1.2),Pi*(4*1.2^28*1.2),t=1.2..1.2],[10 +
6*sin(Pi*t),Pi*(4*t^28*t),t=0..1.25]},style=[point,line],
symbol=[circle,point],coords=polar,
color=[red,blue],symbolsize=[18,1],scaling=
constrained);
This command will plot the trajectory and place a circle
when t = 1.2 s. d) Print out the plot and draw the velocity
vector and its components on the Maple plot at t = 1.2s.
O
θ
B
r
A
D
12 in
O
A
Problem 3.10
The flight path of airplane B is a horizontal straight line
that passes directly over a radar tracking station at A. The
airplane moves to the left with the constant velocity v0.
Determine dθ /dt and d2θ /dt2 in terms of v0 , h , and θ .
θ
vo
C
B
B
h
A
θ
3-53
Problem 3.11
The disk A rotates in a horizontal plane about a vertical axis at a Problem 3.14
& =15 rad/s. Slider B weighs 8 oz and moves A 70-g ball B is given an initial velocity, vo, as shown.
constant rate of θ
o
The ball reaches a height h2 = 0.25 m after bouncing twice
in a frictionless slot cut in the disk. The slider is attached to a from identical 210-g plates. Plate A rests directly on the
spring of constant k = 4 lb/ft, which is undeformed when r = 0. hard ground, while plate C rests on a foam-rubber mat.
Knowing that the disk is released with a zero radial component Determine a) the coefficient of restitution between the ball
of velocity when r = 1 ft, determine the velocity and the normal and the plates, b) the height h of the ball’s first bounce.
1
force between the slider and the slot when r = 0.5 ft.
vo
r
B
slider
O
1.5 m
B
spring
θ& o
Problem 3.12
Two identical cars A and B are at rest on a loading dock
with brakes released. Car C, has been pushed by
dockworkers and hits car B with a velocity of 1.5 m/s.
Knowing that all the cars weigh the same and that the
coefficient of restitution is 0.8 between B and C and 0.5
between A and B, determine the velocity of each car after
all collisions have taken place.
1.5 m/s
A
h1
A
h2
C
foam rubber mat
hard ground
Problem 3.15
Two identical hockey pucks are moving on a hockey rink
at the same speed of 3 m/s and in parallel and opposite
directions when they strike each other. Assuming a
coefficient of restitution of 0.9, determine the magnitude
and direction of the velocity of each puck after impact.
C
B
20°
v
B
Problem 3.13
A 1.3 lb sphere A is dropped from a height of 1.8 ft onto a
2.6 lbf plate B, which is supported by a nested set of
springs and is initially at rest. Knowing that the
coefficient of restitution between the sphere and the plane
is e = 0.8, determine a) the height, h, reached by the
sphere after rebound, b) the equivalent spring constant for
the set of springs if the maximum deflection of the plate is
observed to be 3h.
A
1.8 ft
B
A
v
A
Problem 3.16
A 700-g sphere A moving with a velocity vo parallel to the
ground strikes the inclined face of a 2.1-kg wedge B
which can roll freely on the ground and is initially at rest.
After impact the sphere is observed from the ground to be
moving straight up. Knowing that the coefficient of
restitution between the sphere and the wedge is e = 0.6,
determine a) the angle, θ, that the inclined face of the
wedge makes with the horizontal, b) the energy lost due to
the impact, and c) the impulse acting between the ground
and the wedge B during the impact.
vo
A
B
keq
B
θ
Problem 3.17
The greatest ocean depth yet discovered is in the Marianas
Trench in the western Pacific Ocean. A 29 lb steel ball
released at the surface requires 64 minutes to reach the
bottom. The ball’s experiences a drag force equal to D = 3.02
v where c = 3.02 lb-s/ft and v is the speed of the ball. What is
the depth of the Marianas Trench in miles?
Problem 3.17
A boat is moving to the right with a constant deceleration
of 0.3 m/s2 when a boy standing on the deck D throws a
ball with an initial velocity relative to the deck which is
vertical. The ball rises to a maximum height of 8 m above
the release point and the boy must step forward a distance
d to catch it at the same height as the release point.
Determine (a) the distance d, (b) the relative velocity of
the ball with respect to the deck when the ball is caught.
Problem 3.18
The masses of blocks A, B, and C are mA = 4 kg, mB = 10
kg, and mC = 2 kg. Neglect the masses of the pulleys and
the effect of friction. Assuming the blocks are released
from rest, determine a) the acceleration of each block, b)
the tension in the cords and c) the distance block A will
travel in 2 seconds.
C
Problem 3.20
It is desired to have the package shown deposited on the
horizontal surface with a speed horizontal surface with a
speed of 1.5 m/s. Knowing that r = 0.3 m, (a) determine
the required initial speed v0 when the first loop is used, (b)
show that this requirement cannot be fulfilled by the
second loop, (c) determine the smallest v0 so that the
package will be deposited on the horizontal surface when
the second loop is used.
r
r
v0
v0
Second Loop
First Loop
Problem 3.21
A 3-lb collar is attached to a spring and slides without
friction along a circular rod in a horizontal plane. The
spring has an undeformed length of 6 in. and a constant
k = 1.5 lb/in. Knowing that the collar is in equilibrium at
A and is given a slight push to get it moving, determine
the velocity of the collar (a) as it passes through B, (b) as
it passes through C, (c) the normal force between the rod
and the collar at C.
B
D
A
O
A
C
Problem 3.19
Block B has a mass 10 kg and rests on the upper surface
of a 20-kg wedge, A, as shown. The system is released
from rest and friction is negligible. Determine a) the
acceleration of B, and b) the velocity of B relative to A at
t = 0.5 s.
B
20°
A
5 in
7 in
B
Problem 3.22
To study the performance of a race car, a high speed
camera is positioned at A. The camera is mounted on a
mechanism which permits it to record the motion of the
car as the car travels on straightaway BC. Determine the
speed and the magnitude of the acceleration in terms of b,
Problem 3.24
A 7.92-kg sphere A of radius 90 mm moving with a
velocity v 0 of magnitude v0 = 2 m/s strikes a 720-g
sphere B of radius 40 mm which was at rest. Both spheres
are hanging from identical light flexible cords. Knowing
that the coefficient of restitution is 0.8, determine
a) the velocity of each sphere immediately after impact
b) the impulses in the cables during the impact.
θ, θ& , and θ&& .
v
a
C
θ
b
40 mm
90 mm
B
v0
A
Problem 3.23
A 0.25-lb ball thrown with a horizontal velocity v 0
strikes a 1.5-lb plate attached to a vertical wall at a height
of 36 in. above the ground. It is observed that after
rebounding, the ball hits the ground at a distance of 24 in.
from the wall when the plate is rigidly attached to the wall
(Fig. 1), and at a distance of 10 in. when a foam-rubber
mat is placed between the plate and the wall (Fig. 2).
Determine (a) the coefficient of restitution e between the
ball and the plate, (b) the initial velocity v 0 of the ball.
Answers:
v′A = 1.741 m/s , v ′B = 3.08 m/s
TA∆t = 0.854 N-s, TB∆t = 0 (it will go slack)
1.5 lb
1.5 lb
Foam
pad
vo
vo
0.25 lb
0.25 lb
36 in.
36 in.
24 in.
10 in.
Figure 1
Answer: e = 0.324, v0 = 14.3 ft/s
Figure 2
Problem 3.25
Block A slides down the incline and strikes sphere B
causing it to swing up. The tension in the cable is 100 N
immediately after the impact. Assume the mass of A, mA,
the mass of B, mB, the coefficient of restitution, e, the
coefficient of friction, µk, and the distance, d, are all known.
a) Determine the equations necessary to determine the
initial velocity of A, vo. Neglect the friction
between A and B during the impact.
b) If mA = 1 kg, mB=0.5kg, e = 0.6, µk= 0.35, L = 1.2
m and d = 1.4 m, determine the initial velocity of
A, vo
Problem 3.27
The suspended 10 pound object is initially stationary. The
length of string B is 1.5 ft.
(a) What are the tensions in the strings?
(b) If string A is cut, what is the tension in string B
immediately afterwards?
(c) What is the tension in string B after the mass falls to
the point where the string is vertical, that is, the angle
shown in the figure is 90 degress.
B
`
vo
45°
A
L
A
µk
20°
B
d
Problem 3.26
In the lab you are to design a device for launching a
projectile a maximum distance. This homework problem
is intended to help you in your design.
a)
What is the maximum theoretical velocity the
projectile may have assuming all of the gravitational
energy of the falling block is transferred to the
projectile?
b) Assuming the projectile is launched with a velocity v0
from an elevation, h, as shown, determine the
optimum angle, θ, so that the distance, d, is
maximized.
c) Using the velocity you found in part a) and using h =
10 m, determine the angle, θ, in degrees and the
distance, d.
d) Using your result from part d) what is the radius of
curvature of the path of the particle immediately after
it is launched and at its maximum elevation?
v
θ
h
d
Chapter 4 – Rigid Body Dynamics
In the last chapter we looked at the kinematics and dynamics of particles. In this
chapter we will look at rigid bodies. The kinetics principles we will use to solve
problems are the same: the rate form of conservation of linear and angular
momentum (direct application of Newton’s 2nd Law), the finite time form of linear
and angular momentum (impulse-momentum methods) and the finite time form of
conservation of energy (work-energy methods). We will start by looking at
translation, fixed axis rotation and general plane motion. At the end of the chapter
we will look at kinematics in a more general sense using rotating axes.
4–2
4.1 Introduction
As described in Chapter 1, kinematics is “the geometry of the motion.” Thus far
we have only talked about particles. We are now ready to discuss the kinematics
and dynamics of rigid bodies. A rigid body is an object for which the distance
between any two points on the object is always the same. For now we will limit
our discussion to planar motion. We will start by looking at translation, fixed axis
rotation and general plane motion. The piston-crank system shown in Figure 4.1
illustrates all three types of motion.
1.
2.
3.
Figure 4.1 - Piston-crank
showing translation, fixed
axis rotation and general
plane motion
Translation. If you draw a line between any two points on the object, its
orientation will always stay the same, that is, it will remain parallel to its
original position.
Fixed axis rotation. In this motion, every point on the object travels in a
circle around a fixed point in space.
General plane motion. Any motion that takes place in a plane but is not
translation or fixed axis rotation is called general plane motion.
Translation is usually divided into two categories: 1) rectilinear translation, where
every point travels in a straight line and 2) curvilinear translation, where every
point travels in a curved path. The motion for both of these cases is still translation,
the only difference is that for curvilinear translation, every point will travel in a
curved path as shown in Figure 4.2. Note that even though each particle travels in a
curved path, the object is not rotating.
A
A
A
A
B
B
B
B
Rectilinear Translation
Curvilinear Translation
Figure 4.2 - Translation
In the following sections we will determine how to relate the velocity and
acceleration of various points on a rigid body undergoing translation, fixed axis
rotation and general plane motion. We need to do this because if we want to use
the conservation principles, we need the velocity and/or the acceleration of the
center of gravity.
4–3
Self test on “Identifying the Motion”
Assume the truck shown below is not moving and the links AB and DE are rotating at a constant rate. What is the motion of
a) link AB?
b) link ADF?
c) the crate?
d) If the truck is moving on a flat road, how will your answers change?
e) If the truck is moving, what is the motion of the tire?
0.7 m
B
0.7 m
30°
A
Crate
D
F
a) fixed axis rotation
b) translation
c) translation
d) link AB: general plane motion
link ADF: translation
crate: translation
e) general plane motion
E
4.2 Translation
As mentioned in the last section, translation basically means that the object does
not rotate. If we want to relate the motion of two points on the same rigid body,
such as points A and B in Figure 4.3, we need to define position vectors and
differentiate. We find
r
r
r
rB = rA + rB / A
When we differentiate this we get
Where translation fits
in the kinematics
concept map
A
r
rA
Y
r
rB / A
0
r
r
dr
dr
r
vB = A + B/ A
dt
dt
r
= vA
B
(Magnitude doesn’t change
because it is a rigid body, angle
doesn’t change because the
object is translating)
When we differentiate again we get
r
r
aB = aA
r
rB
X
O
Figure 4.3 - Relating the
motion of two points on a
translating object
In summary we get (which you should have known using your intuition)
r
r
vB = vA
r
r
aB = aA
(4.1) and (4.2)
4–4
In other words, when an object is translating, every point on the object has the same
velocity and acceleration.
So, how do the conservation principles change? They obviously don’t. When
applying the rate form of conservation of linear and angular momentum, it is more
important than ever to draw a free body diagram and a kinetic diagram. On the
kinetic diagram you need to put the acceleration at the center of gravity. We will
therefore have three equations: 1) linear momentum in the x direction, 2) linear
momentum in the y direction, 3) angular momentum about any point. The next few
examples will illustrate this.
Example 4/1
A conveyor system is fitted with vertical panels, and a 0.5 m rod AB
of mass 2.5 kg is lodged between the panels as shown. Assume all the
surfaces are smooth. Given that the acceleration of the panels and the rod
is 1.5 m/s2 to the left, determine the forces on the rod.
A
mrod = 2.5 kg
mpanel = 10 kg
C
a
200 mm
70°
B
Strategy: We are given masses and acceleration and asked for forces, so we need to use LM and AM rate. For a system we should pick
the rod since we are interested in determining the forces on it. We will start by drawing a FBD and KD. Note the direction of the force
at point C is perpendicular to the rod since we are told that the surfaces are smooth.
r
dPx
=
dt
r
∑F
x
→
m rod a = B x − Fc cos 20°
(1)
dt
=
r
∑F
→
y
Fc
mroda
LM y-direction (+↑)
r
dPy
FBD
KD
LM x-direction (+←)
0 = B y − m rod g + Fc sin 20°
mrodg
(2)
Bx
AM about point B (positive CCW)
r
dL B
=
dt
r
∑M
B
→
L
L
0.2
m rod a sin 70° = m rod g cos 70° − Fc
2
2
sin 70°
(3)
By
We have 3 equations and 3 unknowns (Bx, By, Fc) which we can solve by hand or with Maple. We get
Fc = 3.43 N ∠20 o
B x = 6.87 N ←
B y = 23.35 N ↑
When we wrote our equations we assumed the thickness of the rod was small. If it had been thick the moment arms would have been
slightly different.
4–5
Example 4/2
The uniform 60 lb log is supported by two cables and used as a battering ram. If the log is released from rest in the position shown,
determine the tension in each cable immediately after release.
Note: Save all your calculations until after you have derived the
necessary equations.
2’
2’
60°
60° 1’
2’
A
60 lb
B
C
Strategy: We are asked to find tensions and acceleration, so we need to use LM and AM rate.
The first thing we need to do is to draw a FBD and KD. It is important to note that the log will be undergoing translation, so to find the
direction of the acceleration of the center of gravity all we need is the direction of the acceleration of any other point on the object, that
is, point A or point B. Point A will travel in a circle, so it will have two components of acceleration: normal acceleration = v2/r = 0
(since it is released from rest) and tangential acceleration, which will be perpendicular to the wire. The completed FBD and KD are
shown below.
KD
System=log
LM t-direction (see picture for positive direction)
r
dPt
=
dt
∑
r
Ft
ma = mg sin (30°)
→
(1)
n
LM n-direction (see picture for positive direction)
r
dPn
=
dt
r
∑F
→
n
0 = TA + TB − mg cos(30°)
(2)
ma
30°
t
TA
FBD
TB
60°
30°
60°
mg
AM about point G (positive CW)
r
dL G
=
dt
r
∑M
G
→
0 = (TA sin(60°))(1.5 ft ) − (TB sin(60°))(0.5 ft )
(3)
We could have taken moments about any point we like, but for this problem the center of gravity is probably the easiest. If we had taken
moments about a different point (we don’t actually need to do this, I just want to make sure that you could!), say point A, we would have
gotten:
r
dL A
=
dt
r
∑M
A
→
(ma sin 30°)(1.5 ft) = mg(1.5 ft ) − (TB sin 60°)(2 ft )
Again, this was just to illustrate how we would take moments about a different point. We only need Eqs. 1 - 3 to solve for the three
unknowns, TA, TB and a. Solving by hand or in Maple we get:
TB = 38.97 lbf, TA = 12.99 lbf and a = 16.1 ft/s2 at -30° from horizontal.
4–6
4.3 Rigid Body Rotation
In this section we will begin discussing rigid bodies that rotate. We need to start by
giving the basic kinematic relationships.
4.3.1 Basic Kinematic Relationships
r
The quantities we use to describe angular motion are angular position, θ , angular
r
r
velocity, ω , and angular acceleration, α . Analogous equations to the kinematic
equations for rectilinear motion can be written for these quantities.
r
r dθ r&
ω=
=θ
(4.3)
dt
and
r
r dω r&
α
=
=ω
(4.4)
Axis of rotation
dt
The direction of these vectors is perpendicular to the plane of motion and is given
Angular velocity
by the right hand rule (curl the fingers of your right hand in the direction of the
vector
motion and your thumb gives you the direction of the vector) as shown in Figure
Direction 4.4. These equations are analogous to the relationships you already know for
of rotation
position, velocity and acceleration of a point as shown in Table 4.1. In this case,
we are talking about rotation of an object. Therefore, a point on the object does not
have an angular velocity or an angular acceleration. The point has a velocity and
Figure 4.4 - To obtain the direction
acceleration, it is the rigid body itself that has the angular velocity and/or angular
of the angular velocity, use the right
acceleration.
hand rule
Table 4.1 - Basic kinematic relationships
For a point
dx
v=
= x&
dt
dv d 2 x
a=
=
= &x&
dt dt 2
or
a=v
dv (From using
dx the chain rule)
For a rigid body
dθ &
ω=
=θ
dt
dω d 2 θ &&
α=
= 2 =θ
dt
dt
or
α=ω
dω
dθ
(From using
the chain rule)
To obtain algebraic relationships, separate variables and integrate. If the angular
acceleration is a constant, we can separate variables and integrate to get equations
analogous to those obtained for rectilinear motion as shown in Table 4.2.
Table 4.2 - Constant acceleration and constant angular acceleration equations.
a = constant
1
x = x 0 + v 0 t + at 2
2
v = v 0 + at
α = constant
1
θ = θ 0 + ω 0 t + αt 2
2
ω = ω 0 + αt
v 2 = v 02 + 2a ( x − x 0 )
ω 2 = ω 02 + 2α(θ − θ 0 )
4–7
Example 4/3
As steam is injected into a turbine, the angular velocity of the rotor is observed to increase linearly with time. If the rotor starts from rest
and after 8 s has completed 25 revolutions, determine
a) the angular velocity of the rotor at t = 10 s
b) the time required for the rotor to complete 50 revolutions.
Strategy: This is a pure kinematics problem since we are not given any information about what is causing the motion or the mass
properties of the system.
We are given that the angular velocity increases linearly with time. We can write this as an equation
ω = Ct
(1)
where C is an unknown constant. Using our kinematic relationship we get
ω=
dθ
= Ct
dt
θ
t
Separating variables and integrating we get
∫ dθ = ∫ Ctdt
0
0
(2)
1
θ = Ct 2
2
We know θ when t = 8 seconds so we can solve for C.
C=
2θ
t
2
=
2(25rev)(2π rad/rev)
(8s) 2
= 4.91 rad/s 2
We can now solve a) and b) of the problem. Substituting t = 10 s into Eq. 1 (using the value of C we determined) we get
ω = 49.1 rad/s at t = 10 s
Solving Eq. 2 for t and substituting in θ = 50 revolutions = 100π rad we get
t=
2θ
=
C
2(100π rad)
4.91 rad/s 2
→ t = 11.3 s
4–8
Example 4/4
In an investigation of whiplash resulting from rear end collisions, rotation of the head is
of primary interest. An impact test was performed and it was found that the angular
acceleration of the head is
θ
α = 700 cosθ + 70 sinθ
Vertical
G
Assuming the head is initially at rest,
a) Plot the angular velocity as a function of θ for θ = 0 to 45°
b) Determine the angular velocity of the head at θ = 45°
r
O
aO
Strategy: Since we are given angular acceleration and we want angular velocity this is a pure kinematics problem.
The kinematic relationship between angular velocity and angular acceleration is
α=
dω
dt
Substituting in for α we get
α=
dω
= 700 cos θ + 70 sin θ
dt
We need to separate variables and integrate to get ω, but we can’t do this because we don’t have a “dθ”. What do we do? Use the chain
rule as shown below.
dω dθ
dω
= 700 cos θ + 70 sin θ
→ ωdω = (700 cos θ + 70 sin θ)dθ
=ω
dt dθ
dθ
Integrating we get
ω
∫
θ
ωdω =
0
1 2
ω
2
∫ (700 cos θ + 70 sin θ)dθ
0
ω
0
= (700 sin θ − 70 cos θ) 0
θ
1 2
ω = 700 sin θ − 70 cos θ + 70
2
Solving for ω
ω = 1400 sin θ − 140 cos θ + 140
A plot of this is shown to the right and when we substitute θ = 45° we get
ω = 32.11 rad/s
4–9
4.3.2 Fixed Axis Rotation
P3
P4
P2
P1
ω
Figure 4.5 - For fixed axis rotation
every point travels in a circle
Y
y
OXY =
Oxy =
The plane of the motion is perpendicular to the fixed axis. From the discussion in
the previous section we know that a rigid body has an angular velocity and an
angular acceleration. The question we are faced with now is how do we calculate
the velocity or acceleration of a point on the rigid body. If we are going to use the
rate form of conservation of linear momentum (direct application of Newton’s 2nd
law), we will obviously need the acceleration of the center of gravity and if we are
going to use conservation of energy, we need the velocity of the center of gravity.
There are a number of ways to derive the equation for the velocity of any point on a
rigid body that is undergoing fixed axis rotation. We will start by using a vector
differentiation approach and then we will use polar coordinates.
Vector differentiation approach
r
The derivative of any vector Q is equal to
x
O
The description of fixed axis rotation is simple: the rigid body has a hinge, joint, or
pivot which is connected to a non-moving foundation. The rigid body rotates about
a stationary axis passing through this fixed point. There is one point on the rigid
body that has zero velocity, and it is of course this fixed point. All other points
belonging to the rigid body move in circular arcs about the fixed point. The paths
of four points on a rigid body undergoing fixed axis rotation are shown in Figure
4.5.
r
r
r v
dQ
dQ
=
+ ω× Q
dt OXY
dt Oxy
θ
X
Angular velocity of
rotating frame
Time derivative in rotating
frame
Time derivative in fixed
reference frame
inertial reference frame
reference frame attached
to the body and rotating
Figure 4.6 - Coordinate systems
where OXY and Oxy are shown in Figure 4.6. We will be discussing the use of
this equation much more when we discuss the use of rotating coordinate systems.
Therefore, to find the velocity of any point on the object we can define a position
vector and differentiate.
r
Position vector to point A: rA / O
Velocity:
r
dr
r
vA = A/O
dt
Acceleration:
r
dv A
r
aA =
dt
OXY
=
OXY
r
dv A
=
dt
r
d rA / O
dt
Oxy
Oxy
0 since the position between two points
on a rigid body does not change
r r
r r
+ ω × rA / O = ω × rA / O
(4.5)
r r
r r
r r r
+ ω × v A = α × rA / O + ω × (ω × rA / O )
(4.6)
Note that the acceleration has two terms: one points in the tangential direction, (the
r r
α × rA / O term) and one points straight from the point back towards the origin, (the
r r r
ω × (ω × rA / O ) term).
4–10
Derivation using polar coordinates:
Recall from the discussion of polar coordinates
r
v = r&eˆ r + rθ& eˆ θ
r
a = &r& − rθ& 2 eˆ + r&θ& + 2r&θ& eˆ
(
) (
)θ
r
Now if we consider a point on a rigid body undergoing fixed axis rotation we know
that r does not change magnitude so r& = &r& = 0 and since θ& = ω, &θ& = α these
equations reduce to
r
v = rωeˆ θ = rωeˆ t
r
a = −rω 2 eˆ r + rαeˆ θ = rω 2 eˆ n + rαeˆ t
which is identical to what we had before if we recognize that for fixed axis rotation
(circular motion of every point), the unit vector in the transverse direction is
identical to the tangential unit vector and the unit vector in the radial direction is
equal to the negative of the unit vector in the normal direction.
These equations can also be derived using the formulas for velocity and
acceleration in normal and tangential coordinates.
Summary
1. There can be an acceleration component perpendicular to the radius vector
with magnitude rα . We will call it the tangential acceleration.
2.
If there is an angular velocity present, there will always be an acceleration
component with a magnitude rω 2 . The direction of this acceleration is always
in exactly the opposite direction of the radius vector. This component is called
the normal component.
Visual Summary: The velocity and acceleration of a point on a rigid body
undergoing fixed axis rotation is shown below.
Velocity
αr
ωr
ω
Acceleration
P
r
Vector approach:
r r
r
v P = ω × rP / O
Scalar approach:
magnitude = ωr
direction = perpendicular
to r
P
2
ωr
α
ω
Vector approach:
r
r r
r r r
a P = α × rP / O + ω × (ω × rP / O )
r r
r
= α × rP / O − ω 2 rP / O (plane motion)
Scalar approach:
tangential component = αr
normal component = ω2r
Figure 4.7 - Summary of equations for the velocity and acceleration of a
point on an object undergoing fixed axis rotation.
4–11
Example 4/5
A 1.25 m rod is pivoted at one end and swings in the xy plane. At a certain instant, it is oriented at 20 degrees counterclockwise from
the positive x-axis. It has an angular velocity of 0.6 rad/s and an angular acceleration of 0.75 rad/s2, both clockwise. Find the velocity
and acceleration of the free end of the rod.
Strategy: Since we are given the angular velocity and acceleration and there is no indication of what forces are acting on the body to
cause this motion, it appears that this is a pure kinematics problem.
A picture of the rod is shown below.
acceleration
velocity
ω2r
ωr
αr
20°
20°
0.75 rad/s2
0.6 rad/s
0.6 rad/s
The velocity is v = ωr = (0.6 rad/s)(1.25 m) = 0.75 m/s down at an angle of 70° from horizontal left. The normal acceleration is an = ω2r
= (0.6 rad/s)2(1.25 m) = 0.45 m/s2 and at = αr = (0.75 rad/s2)(1.25 m) = 0.934 m/s2. At this point we can resolve these vectors into x and
y components or we could give the acceleration as a magnitude and as a direction. Doing this will be left to the reader. This could
easily be made into a kinetics problem by asking you what forces and moments would need to be acting on the rod at this instant. To
solve this you would need to be given the mass properties of the bar.
Example 4/6
The crate has a weight of 75 kg and rests on the floor of a truck elevator for which the coefficient of static friction is µs = 0.4. Determine
the largest angular acceleration α, starting from rest, which the parallel links AB and DE can have without causing the crate to slip. No
tipping occurs.
0.7 m
B
E
30°
0.7 m
Strategy: This problem involves forces so we will use LM rate. We will need to draw a
FBD and a KD. To draw the KD we should recognize that the crate will be undergoing
translation. We know this because the bottom of the crate (and the L shaped lift) will
always be parallel to the ground. For this reason, the acceleration of the center of
gravity of the crate will be the same as the acceleration of point A, which we can note is
traveling in a circle about point B. It will therefore have a tangential and a normal
acceleration component as shown. Note that r = 0.7 m.
A
Crate
D
B
a n = ω 2 r = 0 (since it starts from rest)
at = αr
A
4–12
We can now draw the FBD (assuming the box is about to slip) and the KD for the crate.
r
dPx
=
dt
∑F
x
→
FBD
KD
LM x-direction (+ →)
m(αr ) cos 30° = µ s N
(1)
m(αr)sin30° = N − mg
(2)
30°
LM y-direction (+↑)
r
dPy
dt
=
∑F
y
→
mg
m(αr)
µsN
System = crate
N
So we have two equations and two unknowns and can solve for α and N. We find
α = 8.42 rad/s2
4.3.3 Comments on applying the conservation principles
F
Conservation of Linear and Angular Momentum (rate)
r
When you draw the kinetic diagram (KD) be sure to include ma G and IGα. IG is
F
called the mass moment of inertia. The mass moment of inertial of some common
shapes are shown in Appendix A. The constraints on the problem may permit you
r
to limit the direction of a . For example:
r
• Translation (α = 0): Put a in the known direction recognizing that the
acceleration of the center of gravity is equal to the acceleration of any other
point on the body.
• Fixed axis rotation: Put tangential acceleration (αr) and normal acceleration
(ω2r) in known directions. Be sure IGα and m(αr) are consistent with each
other.
I Gα
For this special case of fixed axis rotation, it is important to note that conservation
of angular momentum can be simplified. If we take moments about the fixed point
Oy
W
O we will get
r
m(ω2r)
r
dL sys0
=
Mo
Ox
dt
Free Body
Kinetic
where
Diagram (FBD)
Diagram (KD)
dL sys O
= I G α + m (α r ) r
dt
= (I G + mr 2 )α
Figure 4.8 - Free body diagram
but using the parallel axis theorem we know I O = I G + mr 2 . Therefore, for fixed
and kinetic diagram for an object
undergoing fixed axis rotation
axis rotation
dL sys O
= IOα
dt
so conservation of angular momentum (rate form) is
m(αr)
∑
IOα =
∑M
o
4–13
It is important to note that this equation is only valid for fixed axis rotation (or if
point O is the center of gravity).
Conservation of Energy
As you already know, the finite time form of conservation of energy for an
adiabatic closed system is
(4.7)
∆E sys = W
You already know how to use this equation for particles. The only difference when
applying conservation of energy to a rigid body is that there may be moments
acting on it so we need to know how to calculate the work of a moment. Recall
that for a force the work is
2
r r
W = F ⋅ ds
∫
(4.8)
1
Since the work of a force is basically the force times the distance through which it
acts, it makes sense that for a moment we would just need to take the moment times
the angle as shown in Eq. 4.9
2
∫
W = Mdθ
(4.9)
1
So we now know how to take care of the right hand side of Eq. 4.7. You already
know that the energy of a system is:
E sys = E k + E G + E s + U
where
EG = mgz
Es =
(z is the distance from the center of mass to the datum)
1 2
kx (x is measured from the free length of the spring)
2
U = internal energy (this is usually zero in this class unless there is an impact)
The only thing that has really changed (other than having to be careful about using
the change in height of the center of gravity for a system) is in the determination of
the kinetic energy. For a rigid body undergoing fixed axis rotation (or general
plane motion for that matter) the kinetic energy is
Ek = kinetic energy =
1
1
mv G2 + I G ω2 for each rigid body in the system (4.10)
2
2
Note that there will almost always be a kinematic step of relating vG to ω.
For the case of fixed axis rotation, we know vG = rω where r is the distance from
the center of gravity to the fixed point. Again, using this kinematic relationship
4–14
between vG and ω for the special case of fixed axis rotation, the kinetic energy can
be written as
1
1
E k = mv G2 + I G ω2
2
2
1
1
1
= m(ωr) 2 + I G ω2 = (mr 2 + I G )ω2
2
2
2
1
= I O ω2
2
There is no box around this equation because it is for the special case of fixed axis
rotation. Equation 4.10 is a much better equation to know since it is applicable for
fixed axis rotation or general plane motion.
Conservation of Linear and Angular Momentum (finite time)
When you draw the impulse-momentum diagrams as shown in Fig. 4.9, you will
need to include IGω terms. Similar to conservation of energy, there will generally
be a step of kinematics where you will need to relate vG and ω.
mv G 1
mv G 2
I G ω2
In Words:
Equations:
System momentum after the
time interval
r
Psys 2
−
r
L sys O
−
(
=
)
2
I G ω1
System momentum before the
time interval
r
Psys1
=
r
L sys O
=
(
)
1
∫ F dt
1
∫ F dt
2
∫ Mdt
Impulses acting during the time
interval
r
Fi ∆ t ,
r
M O i ∆t
∑
∑( )
Figure 4.9 - Impulse-Momentum diagrams
We therefore have three scalar equations
1. Linear momentum in the x-direction
2. Linear momentum in the y-direction
3. Angular momentum (moment of the momentum) about any axis
Recall:
The finite time form of conservation of linear and angular momentum are typically
used when:
• there is an impact or impulsive forces in the problem
• there are several interacting objects
• there is a force as a function of time
• you want to find velocities, times or forces (especially impulsive forces)
4–15
Example 4/7
A bar of length L and mass m is released from rest at θ = 0.
a) Determine the equations necessary to find the reactios at point A
as a function of θ.
b) Solve the equations you obtained in part a) for m = 2 kg and
L = 0.5 m for θ = 0 to 180°
A
θ
Strategy. Since we want reaction forces we will use LM and AM rate. We may need another principle later, but let’s start with this.
We will draw the FBD and KD at some arbitrary angle θ. We need to recognize that since this is fixed axis rotation, the acceleration of
the center of gravity will have a tangential component (αr) and a normal component (ω2r). In this problem r = L/2.
LM x-direction (+←)
r
dPx
=
dt
∑
r
Fx
→
KD
mω 2 r cos θ + mαr sin θ = − A x
dt
=
r
∑F
→
y
2
m(ω r)
mω 2 r sin θ − mαr cos θ = A y − mg
(2)
r
∑M
Where I G =
G
→ IGα = A y
θ
θ
I Gα
θ
m(αr)
AM about point G (positive CW)
r
dL G
=
dt
L
L
cos θ + A x sin θ
2
2
Ay
(1)
LM y-direction (+↑)
r
dPy
FBD
Ax
mg
(3)
1
mL2 for a slender rod (found from in Appendix A). We now have 3 equations and 4 unknowns (Ax, Ay, α, ω). We
12
need another equation. Where do we get one? We usually look at either kinematics, another system, another conservation principle, or
look in the problem statement to see if we are given anything else. In this problem we are told that the bar is released when θ = 0, so we
can use conservation of energy. The two positions we are considering are shown below. Conservation of energy is:
position 1
E sys2 − E sys1 = W
datum
Since we have no work being done in this problem (the reaction forces do
not travel through any distance and we are assuming a frictionless pin), we
get the energy at position one is equal to the energy at position two, that is,
position 2
Esys1 = E sys 2
where
1
1
mv G2 1 + I G ω12 = 0
2
2
= mgz 1 = 0
E k1 =
E G1
1
1
mv G2 + I G ω 2
2
2
L
= mgz 2 = −mg sin θ
2
E k2 =
E G2
(4)
4–16
We now have 4 equations and 5 unknowns (Ax, Ay, α, ω, vG). For our last equation we have a kinematic relationship between the
velocity of the center of gravity and the angular velocity as shown below.
v G = ωr
(5)
We now have 5 equations and 5 unknowns. We can now plug in the parameters (m = 2 kg, L = 0.5 m) and solve with Maple as shown
below.
> m:=2:
L:=0.5:
g:=9.81:
r:=L/2;
IG:=1/12*m*L^2;
r := 0.2500000000
IG := 0.04166666667
> eq1:=m*omega^2*r*cos(theta)+m*alpha*r*sin(theta)=-Ax;
eq2:=m*omega^2*r*sin(theta)-m*alpha*r*cos(theta)=Ay-m*g;
eq3:=IG*alpha=Ay*L/2*cos(theta)+Ax*L/2*sin(theta);
eq1 := 0.5000000000ω 2 cos ( θ ) + 0.5000000000α sin( θ ) = −Ax
eq2 := 0.5000000000ω 2 sin( θ ) − 0.5000000000α cos ( θ ) = Ay − 19.62
eq3 := 0.04166666667α = 0.2500000000Ay cos ( θ ) + 0.2500000000Ax sin( θ )
> Ek1:=0;
Eg1:=0;
Ek2:=1/2*m*vG^2+1/2*IG*omega^2;
Eg2:=-m*g*L*sin(theta);
eq4:=Ek1+Eg1=Ek2+Eg2;
eq5:=vG=omega*r;
Ek1 := 0
Eg1 := 0
Ek2 := vG2 + 0.02083333334ω 2
Eg2 := −9.810 sin( θ )
eq4 := 0 = vG2 + 0.02083333334ω 2 − 9.810 sin( θ )
eq5 := vG = 0.2500000000ω
> sol1:=solve({eq1,eq2,eq3,eq4,eq5},{alpha,omega,vG,Ax,Ay});
sol1 := { Ay = 0.470880000010-8 ( 0.10416666671021 sin( θ )2 + 0.15625000001021 sin( θ )2 cos ( θ )2
+ 0.15625000001021 sin( θ )4 + 0.17361111111020 )
(
0.416666666710 + 0.125000000010 cos ( θ ) + 0.12500000001011 sin( θ )2 ), Ax = −117.7200000
10
11
2
cos ( θ ) sin( θ ) ( 0.41666666671010 + 0.62500000001010 cos ( θ )2 + 0.62500000001010 sin( θ )2 )
,
0.41666666671010 + 0.12500000001011 cos ( θ )2 + 0.12500000001011 sin( θ )2
cos ( θ )
α = 0.49050000001012
,
0.41666666671010 + 0.12500000001011 cos ( θ )2 + 0.12500000001011 sin( θ )2
vG = 2500.000000RootOf( 462962963_Z 2 − 545 sin( θ ), label = _L10 ),
ω = 10000 RootOf( 462962963_Z 2 − 545 sin( θ ), label = _L10 ) }
> assign(%);
> plot(Ax,theta=0..Pi);
> plot(Ay,theta=0..Pi);
4–17
>
The two plots of Ax and Ay as a function of θ are shown above (granted Maple does not give very nicely labeled axes, but we do get the
solution for any angle θ!).
Example 4/8
An L shaped object consists of two slender bars of length l
and mass m welded together. The rod is released from rest at θ = 0.
A
θ
a) Determine the equations necessary to find the reactions at point A
when θ = 90°.
Strategy: Since we need to find reaction force we will need LM and AM rate and because we have two locations we will need
conservation of energy (to find the angular velocity at the bottom). There are really two ways to solve this problem. We could find the
object’s center of gravity, or we can just treat the two bars independently, each having their own center of gravity, but with each bar
having the same angular velocity and acceleration. We will use the
A
B
Datum
second approach.
Let’s start with conservation of energy. We need to draw the system
at the two positions we are interested in, and we can define a datum
for the problem as shown. Conservation of energy is:
E sys2 − E sys1 = W
Since we have no work being done in this problem, we get the
energy at position one is equal to the energy at position two, that is,
r
C
B
Position 2
E sys1 = E sys 2
or
E k 1 + E g1 = E k 2 + E g 2
(1)
0
where
L
E g1 = −m BC g
2
L
E g 2 = −m AB g − m BC gL
2
(2)
(3)
C
Position 1
4–18
1
1
1
1
E k 2 = m AB v G2 AB + I G AB ω 2AB + m BC v G2 BC + I G BC ω 2BC
2
2
2
124444424
4444
3 14444
4244444
3
barAB
(4)
BarBC
In these 4 equations we have 7 unknowns ( E g1 , E g 2 , E k 2 , v G AB , v G BC , ω AB , ω BC ). Where do we look for more equations?
Kinematics! Since we really only have one object, the angular velocities of the two bars are the same.
ω AB = ω BC
(5)
We can also relate the center of gravities of the bars to the angular velocities easily since the object is undergoing fixed axis rotation.
v G AB = ω AB
v G BC = ω BC r
L
2
(6)
(7)
where
L
r = L2 +
2
We now have 7 equations and 7 unknowns and can solve for the angular velocity of the object when it is at position 2. To apply LM and
AM rate, we need to draw a FBD and KD at position 2. Since the object is undergoing fixed axis rotation, for the acceleration of the
center of gravity we will put the normal and tangential components.
y
KD
FBD
x
Ay
Ax
L
m AB ω 2
2
L
m AB α
2
β
( )
m BC ω 2 r
mABg
I G AB α
m BC (αr )
I G BC α
mBCg
Where
I G AB =
1
1
L/2
−1 1
m AB L2 , I G BC =
m BC L2 and β = tan −1
= tan
12
12
2
L
We have 3 additional unknowns in these diagrams, Ax, Ay, and α, and we will get three equations from applying linear momentum in the
x and y directions and angular momentum about some point. These equations are shown below.
LM x-direction (+ →)
LM y-direction (+↑)
dPx
=
dt
dPy
dt
AM about A (positive CCW)
=
∑F
x
∑F
y
dL A
=
dt
→
→
∑M
A
L
m AB α + m BC (αr ) cos β + m BC (ω 2 r ) sin β = A x
2
(8)
L
m AB ω 2 − m BC (αr ) sin β + m BC (ω 2 r ) cos β = A y - m AB g - m BC g (9)
2
→
L
L
I G AB α + m AB α + I G BC α + m BC (αr ) = m BC g
2
2
We now have 10 equations and 10 unknowns and can solve for all of the answers.
(10)
4–19
Example 4/9
The slender bar of mass m = 1.2 kg and length L = 2 m is released from rest in the horizontal position shown. If point A of the bar
becomes attached to the pivot at B upon impact, determine immediately after the impact:
L=2m
a) the angular velocity, ω, of the bar
b) the impulse exerted on the rod at A during the impact.
x = 0.8 m
A
h=1m
B
Strategy: This looks like a two part problem, that is, the bar falls and then the bar hits and sticks to the pivot. For the falling part of the
problem, let’s use conservation of energy (although we could just use projectile motion equations) and for the impact we need LM and
AM finite time. For both parts the bar will be our system.
Falling: The two positions are shown in the figure to the right.
Conservation of energy for a closed system is
1
E sys2 − E sys1 = W
A
2
h=1m
datum
B
Since we have no work being done in this problem, the energy at position
one is equal to the energy at position two, that is,
E sys1 = E sys2
mgh =
1
mv 2
→ v = 2gh = 2(9.81m/s 2 )(1m) = 4.43 m/s = v G1 (velocity before the impact)
2
Impact: Let’s draw impulse-momentum diagrams for the bar as shown below.
-
IGω2
A
A
mv G 2
=
mv G1
Ay∆t
A
Angular momentum about A (positive CW)
I G ω 2 + (mv G 2 )(0.2m) − (mv G1 )(0.2m) = 0
We have two unknowns in this equation, ω2 and v G 2 , since we can find IG for a slender bar using I G =
1
mL2 = 0.4 kg − m 2 . . To
12
generate another equation we use kinematics, that is, we can relate ω2 and v G 2 since after the impact the object will be undergoing fixed
axis rotation. Therefore,
v G 2 = ω 2 (0.2m)
We therefore have two equations and two unknowns and can solve these to get
ω 2 = 2.37 rad/s (Clockwise)
v G 2 = 0.474 m/s (down)
4–20
To find the impulse exerted on the rod, let’s use LM in the y direction.
Linear momentum in the y-direction (+ ↓):
mv G 2 − mv G1 = − A y ∆t
The only unknown in this equation is the impulse, Ay∆t,
A y ∆t = mv G1 − mv G 2
= (1.2kg )(4.43 m/s) − (1.2kg)(0.474 m/s)
= 4.75 N - s (up)
Example 4/10
ω
A slender bar rotates freely in the horizontal plane about a vertical shaft at O.
The bar weighs 10 kg and its length is 1.5 m. The slider A weighs 1 kg and can
be treated as a point mass, that is, the mass moment of inertia about its center
of mass is negligible. If the bar's angular velocity is ω = 10 rad/s and the radial
component of A is zero when r = 0.4 m, calculate the angular velocity of the bar
when r = 1.0 m.
A
O
r
Strategy: We have two locations (r = 0.4 and r = 1.0), so we will need to use conservation of energy and AM finite time.
Let’s start with AM finite and draw impulse-momentum diagrams. Note that for these pictures we will draw them in the same
orientation for convenience, but clearly the angular position would be different at the two times of interest.
m A v A2y
m bar v G1
m bar v G 2
m A v A1
m A v A2x
O
I G bar ω 2
∫O
O
O
A
A
y dt
∫O
I G bar ω1
r1 = 0.4 m
r2 = 1 m
After
Before
x dt
A
r
During
Since we are not interested in the impulses acting at point O, let’s apply conservation of angular momentum, finite time, about point O
∫
∆L sysO = M O dt
we get (assuming positive is counter-clockwise):
L
L
I G bar ω 2 + m bar v G 2 + m A v A 2 y r2 − I G bar ω1 + m bar v G1 + m A v A1 r1 = 0
2
2
(1)
Since we are given ω1 = 10 rad/s and we can find the mass moment of inertia of the bar about its own center of gravity using
IG=1/12mL2, we are left with 5 unknowns in this equation: ω 2 , v G 2 , v A 2 y , v G1 , v A1 . Let’s use kinematics to get additional
equations. Since the bar is undergoing fixed axis rotation, and since at time one collar A has zero radial velocity we get:
v A1 = ω1 r1
(2)
4–21
v G1 = ω1
L
2
(3)
v G2 = ω2
L
2
(4)
v A 2 y = ω1 r2
(5)
and the transverse component of the velocity of the collar will be
We now have 5 equations and 5 unknowns and can solve for the unknowns. We still have one additional unknown velocity component
in our impulse-momentum diagrams, that is, the radial component of velocity. You should be able to determine its magnitude using
conservation of energy.
4.3.4 Rigid Body Impact
n
B
P
A
t
Figure 4.10 - Impact between
two rigid bodies
When considering rigid body impact we have to be careful using the coefficient of
restitution equation. As discussed in section 3.4, the coefficient of restitution uses
the normal components of velocity at the point of contact.
v ′PB n − v ′PA n
e = −
v PB − v PA
n
n
or
(
) (
v ′PB n − v ′PA n = -e v PB n − v PA n = e v PA n − v PB n
where
e = the coefficient of restitution (0 ≤ e ≤ 1)
v′PA n = the velocity of the point of contact on object A in the normal direction
after the impact
v′PB n = the velocity of the point of contact on object B in the normal direction
after the impact
v PA n = the velocity of the point of contact on object A in the normal direction
before the impact
v PB n = the velocity of the point of contact on object B in the normal direction
before the impact
Example 4/11
A 50 gram ball traveling at 20 m/s strikes the homogeneous, long slender
link with mass 1 kg, at a distance, h, below the pin joint A. The coefficient
of restitution between the link and the ball is 0.5.
a) Find the distance h so that the pin reaction in the x-direction will be
zero at the instant of impact.
b) Plot the distance h as a function of the coefficient of restitution for 0<e<1 and
as a function of the initial velocity of B.
c) Plot the reaction force at point A in the horizontal direction as a function of h
when e = 0.5.
A
1m
h
B
Strategy: We have an impact problem, so we will need to use LM and AM finite time. We will also need to use the coefficient of
restitution equation since we are given e. Since we are asked to make some plots we will solve the problem in terms of the initial
velocity of B, vB, h, and e.
)
4–22
Let’s start with impulse-momentum diagrams.
Ay∆t
A
I G L ω′L
m L v ′G L
A
A
h
Ax∆t
h
B
h
B
m B v ′B
B
mBvB
System momentum
before the time interval
System momentum after
the time interval
External impulses acting
during the time interval
We will now apply the finite time version of the conservation of linear momentum in the x direction and angular momentum about point
A.
LM x-direction (+ ← )
∆Psysx =
∑ F ∆t
x
→
(m L v ′G L + m B v ′B ) − m B v B = A x ∆t
(1)
Angular momentum about point A (positive CW)
∆L sysA =
∑M
A ∆t
→
where L = 1 m, mB = 0.05 kg, mL = 1.0 kg, and I G L =
(I G L ω′L + m L v ′G L
L
+ m B v ′B h ) − m B v B h = 0
2
(2)
1
m L L2 . We have 3 equations and 4 unknowns ( v ′G L , v ′B , ω′L , h ) assuming
12
we know Ax∆t = 0 for parts a) and b). We need more equations. Where do we look? Kinematics. Since the link is undergoing fixed
axis rotation we know
L
v ′G L = ω′
2
(3)
We still need one more equation, but fortunately we haven’t used the coefficient of restitution equation yet. As discussed in the last
chapter, I think it is easiest to write this equation in general terms first and then to substitute the variables, and their directions as you
have defined them in your impulse-momentum diagrams. The general equation for the coefficient of restitution for rigid body impact is
v ′PBn − v ′PA n = e( v PA n − v PBn )
For this problem we will define the ball to be object B, the link to be object A and point P is the point of contact between the two.
Substituting in we get
v ′B − v ′P = e(0 − v B )
(4)
We now have 4 equations, but one additional unknown, v ′P , that is, the velocity of the point of contact on the link after the impact.
Again, since the link is undergoing fixed axis rotation, we have a kinematic relationship between the velocity of point P and the angular
velocity of the link.
v ′P = ω′h
We now have 5 equations and 5 unknowns ( v ′G L , v ′B , ω′, h , v ′P ) that we can solve to answer part a) as shown below.
(5)
4–23
Clearly the answer to part a) is h = 0.667 m and it is independent of the initial velocity of B and of the coefficient of restitution so the
plots asked for in part b) would just be straight lines. We also see from the answers that the velocity of the link after the impact is a
linear function of the coefficient of restitution and of the initial velocity of B. To solve part c), we will solve these equations again
except instead of setting equation 1) equal to zero, as was done in the Maple worksheet, we will set it equal to Ax∆t.
Clearly, when h is less than 0.667 m, the reaction is to the left and when it is greater than 0.667 m, the reaction is to the right. The point
where the reaction goes to zero is called the center of percussion.
4–24
4.4 General Plane Motion
Now that you know how to do problems involving translation and fixed axis
rotation, general plane motion should not be a problem since it can be considered as
a translation plus a rotation as shown in figures below.
A2
A2
B1
A1
Where general plane motion
fits in the kinematics concept
map
=
B2
A1
+
B2
or
A 1'
B2
Rotation
about B
Translation
of B
General
Plane
+
B1
A 1'
=
+
Figure 4.11 - Illustrations of general plane motion being a translation plus a rotation
Figure 4.12 - Snapshot from Working Model
4.4.1 Velocity
As discussed in the previous section, general plane motion can be considered a
translation plus a rotation. That is, if two points, A and B, are on the same rigid
body and you are on point A looking at point B, it will appear that B is traveling in
a circle around A. Therefore, the relative velocity of B with respect to A is:
4–25
r r
r
v B / A = ω × rB / A
(4.10)
r
r
This has a magnitude of v B / A = ωrB / A and a direction perpendicular to ω and
r
to rB / A . Thus, for general plane motion we can always relate the velocity of two
points on the same rigid body by using
r
r
r
vA = vB + vA / B
r r
r
= v B + ω × rA / B
(4.11)
The methods to determine the velocity of a point on an object undergoing the three
types of planar motion so far discussed in this text are summarized in Table 4.3.
Table 4.3 - Summary of the types of motion discussed so far
Type of motion
How to find the velocity of a point on the rigid body
1.
Translation
r
r
v B = v A (all points on the rigid body have the same velocity)
2.
Fixed axis rotation
r r
r
v B = ω × rB / A (vector approach) or
v B = ωrB / A with a direction ⊥ to rB / A (scalar approach)
3.
General plane motion
r r
r
a) v B = ω × rB / IC (instantaneous center approach - discussed in the next section)
r r
r
r
b) v B = v A + ω × rB / A (vector algebra)
r r
r
r
c) Vector triangle approach (draw the vector triangle for v B = v A + ω × rB / A )
Let’s look at an example.
Example 4/12
Bar AB rotates with a constant angular velocity of 1600 rev/min
counterclockwise. Determine the velocity of point D at the instant shown.
7″
3″
y
x
A
B
D
P
50°
Strategy: Since we are not asked for forces, or told what is actually causing the motion, we can recognize this problem as a pure
kinematics problem.
Let’s start by identifying the motion. Since point A is fixed, link AB is undergoing fixed axis rotation (good, we know how to deal with
this). Since the piston is constrained to go horizontally, it is simply undergoing translation (HA! no problem – bring it on!), but
unfortunately, the connecting rod, link BD, is undergoing general plane motion (the only really new part of the problem). All we need to
solve this problem is the equation that relates the velocity of any two points on the same rigid body, that is, Eq. 4.11
r r
r
r
v A = v B + ω × rA / B
(4.11)
4–26
I will solve this problem two ways to illustrate the use of this equation and so you will hopefully get a better feel for general plane
motion.
We will start by determining ωAB in rad/s:
rev 1 min 2π rad
ω AB = 1600
= 167.55 rad/s
min 60 s rev
When solving this type of problem, we always start with the link we know something about and then move to the adjacent link, etc.
Method 1: Vector algebra approach
Bar AB is undergoing fixed axis rotation, so the velocity of B can be found using vector algebra or by recognizing that the magnitude of
the velocity is simply v B = ω AB rAB and its direction is perpendicular to bar AB (remember, it is undergoing fixed axis rotation).
Therefore
v B = ω AB rAB = (167.55 rad/s)(3 in ) = 502.66 in/s at 140° up from horizontal.
To confirm this result we can also do this using vector algebra. Let’s use a standard xy coordinate system as shown in the original
figure.
r
r
r
r
v B = v A + ω AB × rB / A
= 0 + 167.55kˆ × (3 cos 50°ˆi + 3 sin 50°ˆj)
= 323.10ˆj − 385.05ˆi in/s
This is the same answer we found using the scalar approach if we resolve it into a magnitude and a direction. Now we need to move on
to bar BD. We just calculated the velocity of one point on the bar, point B, so let’s relate the velocity of B to the velocity of another
point on the bar, but which point? Point D of course! Why? Because we know that the velocity of point D has to be in the horizontal
direction.
Relating the velocity of point D to point B on bar BD we get:
r
r
r
r
v D = v B + ω BD × rD / B
Substituting in what we know, we get
v D ˆi = (−385.05ˆi + 323.10ˆj) + ω BD kˆ × (7ˆi )
= −385.05ˆi + 323.10ˆj + 7ω ˆj
BD
Equating components we get:
ˆi :
v D = −385.05 in/s
(1)
0 = 323.10 + 7ω BD
(2)
ˆj :
We have 2 equations and 2 unknowns which we can solve.
r
v D = −385.05 in/s ˆi = 385.05 in/s (to the left)
r
ω BD = −46.16 rad/s kˆ = 46.16 rad/s (clockwise)
Method 2 – Vector triangle approach
Let’s solve the problem a different way. We will use the same equations, but instead of using vector algebra, let’s just look at the vector
triangle. We solve for the velocity of point B on bar AB the same way we did before, that is, v B = ω AB rAB and its direction is
perpendicular to bar AB. Therefore
v B = ω AB rAB = (167.55 rad/s)(3 in ) = 502.66 in/s at 140° up from horizontal.
Relating the velocity of point D to point B on bar BD we get:
4–27
r
r
r
r
v D = v B + ωBD × rD / B
just like before. Instead of using vector algebra, we can just draw the vector triangle that represents this equation and use geometry to
r
r
solve for the unknowns. Why can we do this? Well, we know the velocity of B, we know the direction of ω BD × rD / B (perpendicular
r
r
to rD / B ) and we know the direction of v D (horizontal). A procedure for the vector triangle approach is shown below:
Step 1: Define a point corresponding to the earth. All absolute velocity vectors must have their tail on the earth.
Step 2: Draw v B = ω AB rB / A perpendicular to link AB
Step 3: Draw v D / B = ω BD rD / B (direction perpendicular to link BD)
Step 4: Draw v D (direction is known to be horizontal)
r
r
r
r
r
r
Step 5: Draw vectors to satisfy v D = v B + v D / B = v B + ω BD × rD / B
I will show you each step of this procedure to demonstrate what I mean.
Step 1:
vB
Step 2:
+
Earth
50°
+
Earth
Direction
of vD/B
Direction
of vD/B
Step 3:
Step 4:
vB
50°
50°
+
Earth
+
Earth
Direction
of vD/B
Step 5:
vB
50°
v D / B = ω BD rB / D
vD
+
Earth
Using the completed vector triangle from Step 5, we see
vB
Direction
of vD
Direction
of vD
4–28
v D = v B sin 50° = 502.66 sin 50° = 385.06 in/s (to the left)
v D / B = ω BD rD / B = v B cos 50° = 502.66 cos 50° = 323.10 in/s
→ ω BD =
The direction of ω BD will be clockwise from the direction of v D / B . These are the same
answers we got using the vector algebra approach.
323.10 in/s
= 46.16 rad/s
7 in
B
D
vD/ B
To be perfectly honest, I prefer the vector algebra approach. It sometimes takes longer, but it always works and the vector triangle
approach can be difficult when the geometry is not fairly simple. Actually, that is not quite true. The velocity problem is usually not too
bad, but if you try to use the vector triangle approach for the acceleration problem (discussed later) it really is a pain. The advantage of
the vector triangle approach is that if the geometry is straight forward you can do problems fairly quickly and also I think it helps you
understand what the terms in the equation actually represent.
Before we look at some more examples, let’s introduce one other concept that
makes some problems easier called the instantaneous center of velocity. It is
important to note right from the start that the instantaneous center of velocity
cannot be used for accelerations!
4.4.2 Instantaneous Center of Velocity
The instantaneous center of velocity (IC) is a unique reference point which
momentarily has a velocity of zero. Thus, as far as velocities are concerned, the
body seems to rotate about the instantaneous center, that is, the velocity of any
point on the rigid body is simply the angular velocity of the rigid body times the
distance to the IC ( v P = ωrP / IC ).
How to find the IC
If there is a fixed point on the object, or a point that has a velocity of zero, this
point is the instantaneous center of velocity. To find the instantaneous center of
velocity in the case where there is not a fixed point, you need to know the direction
of the velocity of two points. We’ll look at some examples to illustrate this. All
you need to do to find the IC is to draw a line perpendicular to the velocity and
through the two points. Three cases are illustrated below in Figure 4.13. Case 1 is
the easiest because you have two distinct lines that clearly intersect. This would be
the case for general plane motion. The intersection point is the IC. In Case 2 when
we draw a line perpendicular to the velocity and through points A and B we only
get one line. To get another line we connect the tips of the velocity (which means
we need to know them!). This would be the case for fixed axis rotation or for an
instant of general plane motion. In Case 3 we get two parallel lines indicating that
the IC is at infinity, that is, at this instant the object has an angular velocity of zero.
This is the case for translation or for an instant of general plane motion.
4–29
Case 1
Case 2
A
A
IC
Case 3
B
A
B
No IC
at this
instant
B
IC
An instant of general
plane motion
Fixed axis rotation or an
instant of general plane motion
Translation or an instant of
general plane motion
Figure 4.13 - Illustration of how to determine the
location of the instantaneous center of velocity.
The final situation you may encounter is when you have the velocity of one point
and the angular velocity of the body. In this case you can also find the IC since you
know v P = ωrP / IC . You can determine rP / IC from this equation and you know that
the IC lies along a line perpendicular to v P.
Observations:
• The instantaneous center may lie off the body.
• Once the instantaneous center is found the absolute velocity of any point on the
body is readily determined.
• The acceleration of the instantaneous center is not zero (in general) so it cannot
be used to find the acceleration of points on the rigid body.
• For rolling without slipping on a fixed surface, the IC is the point of contact
(because the ground doesn’t move and there is no slipping, the point in contact
has the same velocity as the ground, that is, zero). Figure 4.14 shows 4
snapshots of an object rolling without slipping. Notice the velocity of any
point is perpendicular to a point drawn from the point of contact to the point of
interest.
For rolling without slipping
on a fixed surface, the IC is
at the point of contact.
Note the velocity in
all the instances
shown is
perpendicular to a
line drawn from the
point of contact to the
point of interest.
Figure 4.14 - Snapshot of an object rolling in Working Model
In the four snapshots shown in Figure 4.15 we have four instances of motion for a
four bar linkage (yes, I know there are only three bars - they are still called four bar
linkages!). The two short links have pinned ends and the upper link is driven at a
constant angular velocity. We know the direction of the velocity of the two end
points of the connecting bar because of the two short links undergoing fixed axis
rotation. We draw lines perpendicular to these two directions and where these lines
4–30
cross is the location of the instantaneous center. Notice how the IC is at different
locations depending on the orientation of the linkages. The velocity of several
other points on the connecting link are also shown to illustrate the usefulness of the
IC. Once the IC is found, the velocity of any point is simply the angular velocity of
the connecting link times the distance to the IC and the direction is perpendicular to
the line from the IC to the point of interest.
IC
IC
no IC at
this
IC
Figure 4.15 - Four snapshots of a four bar linkage in Working Model
showing the location of the instantaneous center of velocity
Check your understanding:
A rigid body has velocities VA and VB as shown.
a) Which labeled point on the body will have the greatest velocity?
b) Which point will have the smallest velocity at this instant?
E
F
VA
A
C
Answer:
B
VB
a) F
b) C
D
4–31
Example 4/13
The rod AB is attached to two uniform disks as shown below. A constant force, F, is applied to point B causing the disks to roll without
slipping on the ground. Knowing that all the objects are initially at rest, determine the equations necessary to find the angular velocities
of each of the objects after disk 1 rotates through 90 degrees.
Radius = r
Mass = m1
Radius = r
Mass = m2
Length = L
Mass = mbar
A
B
No
slipping
F
Disk 1
Disk 2
Strategy: We have two positions, so we need to use conservation of energy. We will also have to do some kinematics to relate the
velocities and angular velocities of the three objects. For our system we will pick both disks and the bar.
We will start by drawing the system in the two positions. The second position is drawn with dotted lines.
A
B
datum
F
Writing conservation of energy we get
E sys2 − E sys1 = W
or
(E k
where
2
) (
)
+ E g 2 − E k1 + E g1 = W
0
0
(1)
r
E g1 = m bar g
2
(2)
1
1
1
1
1
1
E k 2 = m bar v G2 AB + I G AB ω 2AB + m 1 v G2 1 + I G1 ω12 + m 2 v G2 2 + I G 2 ω 22
2
2
2
2
2
2
14444
4244444
3 1444
424444
3 1444
424444
3
(3)
W = Fs
(4)
barAB
Disk 1
Disk 2
and the work is
1
1
1
m 1 r 2 , I G 2 = m 2 r 2 , and I G AB =
m bar L2 . In Eqs. 1-4 we have 10 unknowns:
2
2
12
W , E k 2 , E g1 , v G AB , ω AB , v G1 , ω1, v G 2 , ω 2 , s . The distance s can be found from the figure showing the two positions using a bit of
The mass moments of inertia are I G1 =
geometry:
π
s = + L + r − L2 + r 2
2
(5)
4–32
For the rest of the equations we need, let’s go to kinematics. Since the disks roll without slipping on the ground, their instantaneous
centers of velocity are the points of contact with the ground. This gives
Disk 1:
v G1 = ω1 r
(6)
Disk 2:
v G2 = ω2 r
(7)
To relate the velocity of the center of gravity of the bar to its angular velocity, we need to find the bar’s instantaneous center. We know
the direction of the velocity of two points on the bar, A and B, from the disks as shown below. From this figure it is clear that
L
v G AB = ω AB L2 +
2
2
ICbar
(8)
We still need more equations, but knowing the IC of the bar we can
find the velocities of point A and B
v G 2 = ω AB L
L
(9)
Disk 1
v A = ω AB L 2
(10)
A
L
We have one more unknown, vA, but we can relate the velocity of
point A to the angular velocity of disk 1 using
v A = ω1 r 2
B
Disk 2
(11)
We now have 11 equations and 11 unknowns and can solve.
Example 4/14
Gear C has a mass of 3.2 kg and a centroidal radius of
gyration of 0.06 m. The uniform bar AB has a mass of 2.4 kg,
and gear D is stationary (only part of gear D is shown). If the
system is released from rest in the position shown, determine the
equations necessary to solve for the angular velocities of gear C
and bar AB after AB has rotated through 90°.
160 mm
A
C
B
80 mm
D
Strategy: We have two locations in space, so we will use the finite time form of conservation of energy for a closed system. For the
system we will pick both the disk and the bar.
Before we apply the conservation principle, let’s do some background calculations. Using the centroidal radius of gyration we get
I G C = m C k G2 C and I G AB =
1
m AB L2 .
12
4–33
Conservation of Energy: E sys2 − E sys1 = W
The only external forces we will have on our system will be the pin forces at point A
and the forces between gear D and C. Since these do not travel through any distance,
W = 0 so we get
position 1
C
B
E sys1 = E sys2
A
or
E k 1 + E g1 = E k 2 + E g 2
0
L
datum
r
(1)
0
where
position 2
L
− m C gL
2
1
1
1
1
= m AB v G2 AB + I G AB ω 2AB + m C v G2 C + I G C ω C2
2
2
2
2
144444244444
3 1444424444
3
E g 2 = −m AB g
(2)
E k2
(3)
bar
disk
So, right now we have 3 equations and 6 unknowns ( E g1 , E k 2 , v G
AB
, ω AB , v G , ω C ). Where do we get more equations?
C
Kinematics! Bar AB is undergoing fixed axis rotation so we get
v G AB = ω AB
L
2
(4)
and
v G C = ω AB L
(5)
The instantaneous center for gear C is the point in contact with D giving
v GC = ωC r
(6)
Now we have six equations and six unknowns which we can solve using Maple. The Maple worksheet is shown below.
> mC:=3.2:
kGC:=0.06:
mAB:=2.4:
L:=0.16:
r:=0.08:
g:=9.81:
IGAB:=1/12*mAB*L^2;
IGC:=mC*kGC^2;
IGAB := 0.005120000000
IGC := 0.01152
> eq1:=0=Ek2+Eg2;
eq2:=Eg2=-mAB*g*L/2-mC*g*L;
eq3:=Ek2=1/2*mAB*vG[AB]^2+1/2*IGAB*omega[AB]^2+1/2*mC*vG[C]^2+1/2*IGC*omega[C]^2;
eq4:=vG[AB]=omega[AB]*L/2;
eq5:=vG[C]=omega[AB]*L;
eq6:=vG[C]=omega[C]*r;
eq1 := 0 = Ek2 + Eg2
eq2 := Eg2 = -6.906240000
2
2
2
eq3 := Ek2 = 1.200000000vGAB + 0.002560000000ω AB + 1.600000000vGC + 0.005760000000ω C
2
4–34
eq4 := vGAB = 0.08000000000ω AB
eq5 := vGC = 0.16 ω AB
eq6 := vGC = 0.08 ω C
> solve({eq1,eq2,eq3,eq4,eq5,eq6});
{ Eg2 = -6.906240000, Ek2 = 6.906240000, ω C = -19.28998311, vGAB = -0.7715993243, ω AB = -9.644991554,
vGC = -1.543198649}, { Eg2 = -6.906240000, Ek2 = 6.906240000, ω C = 19.28998311, vGAB = 0.7715993243,
ω AB = 9.644991554, vGC = 1.543198649}
So our final answers are: v G AB = 0.77 m/s ←, ω AB = 9.64 rad/s (CW), v G C = 1.54 m/s ←, ω C = 19.29 rad/s (CCW)
Example 4/15
A student at graduation is so excited the he tosses his laptop into the air.
When the laptop reaches its maximum height it has an angular velocity
of 6 rad/s and a disgruntled student (who was dropped from the Institute
for academic misconduct) shoots the laptop with a high powered rifle as
shown below. The bullet strikes the laptop with a speed of 1500 ft/s and
exits with a speed of 800 ft/s. Assume the bullet leaves at the same angle
it enters the laptop. The bullet weighs approximately 1-oz (0.002 slugs),
the laptop weighs 10 lbs (0.31 slugs) and has a mass moment of inertia about
its center of gravity of 0.0256 slug-ft2.
Determine:
a) the angular velocity of the laptop after the bullet has passed through it
b) the location of the instantaneous center of velocity immediately after impact
0.5 ft
6 rad/s
30°
1500 ft/s
Strategy: We have an impact, so we should use LM and AM finite time. As a system we will pick both the bullet and the laptop.
We will start by drawing impulse-momentum diagrams. Since it is not clear in which direction the laptop will move after the impact
(you actually should be able to reason it out, but why bother?) we will represent the velocity of the laptop after the impact in terms of x
and y components. Our equations are:
(
r
L sysO
m B v ′B
30°
-
m L v ′G y
I G ω′
r
r
Psys2 − Psys1 =
r
− L sysO =
) (
2
r
∑ Fr∆t
) ∑ (M ) ∆t
i
O i
1
=
I G ω1
m L v ′G x
30°
m B v B1
System momentum before the
time interval
System momentum after the
time interval
External impulses acting during the
time interval
LM x-direction (+ → )
∆Psysx =
∑ F ∆t
→
(m L v ′G x − m B v ′B sin 30°) − (−m B v B1 sin 30°) = 0
(1)
∆Psys y =
∑ F ∆t
→
(m L v ′G y + m B v ′B cos 30°) − (m B v B1 cos 30°) = 0
(2)
x
LM y-direction (+↑ )
y
4–35
Angular momentum about the center of gravity of the laptop (positive CW)
∆L sysG =
∑M
G ∆t
→
(I G ω′ − rm B v ′B cos 30°) − (I G ω1 − rm B v B1 cos 30°) = 0
(3)
where r = 0.5 ft. We have 3 equations and 3 unknowns and can solve for v ′G x , v ′G y , ω′ using Maple (or by hand) as shown below.
So, ω′ = 17.66 rad/s (CCW), v G x = 2.26 ft/s ←, v G y = 3.91 ft/s ↑
The second part of the problem asks for the location of the instantaneous center. Why would we want to know its location? I have no
idea, but it does make for an interesting part b) and tests how well we understand what an IC is! To find the instantaneous center all we
need to do is to recognize that v ′G = ω′rG / IC and to find the magnitude and direction of the velocity. If we find the magnitude and
direction of the velocity we get
r
v ′G = 4.52 ft/s
30°
This makes sense if we think about it. The initial momentum of the system is in the original direction the bullet was flying, so it makes
sense that the laptop would end up traveling in that direction. Using the definition of instantaneous center we get
rG / IC =
v ′G
4.52 ft/s
=
= 0.256 ft
ω′ 17.66 rad/s
Since the final angular velocity is counterclockwise, we know the location of the IC will be below and to the left of the laptop as shown
below.
0.256 ft
30°
IC
4–36
Example 4/16
ω
A thin ring having a mass of 15 kg strikes the 20-mm high step.
The mass moment of inertia of a ring is mr2. Determine the
smallest angular velocity ω the ring can have so that it will
make it over the step. Assume the ring does not slip or rebound
from the step.
180 mm
20 mm
Strategy: The problem starts with an impact, so we need to start with LM and AM finite time. After the ring imbeds on the corner and
as it rotates up to the top, we can use conservation of energy. Our system will be the ring.
Let’s start with some background calculations. IG = mr2 = (1.5 kg)(0.02m)2 = 0.006 kg-m2. To use LM and AM finite time we start with
impulse-momentum diagrams. Our two times will be right before the impact and right after the corner is imbedded into the ring. After
the impact the disk will undergo fixed axis rotation, so the velocity of the center of gravity will be perpendicular to a line drawn from the
contact point to the center of gravity.
mv′G
IG ω
-
I G ω′
mv G
A
=
Ax∆t
A
A
Ay∆t
We don’t care what the reaction impulses are at the contact point, so we will apply conservation of angular momentum about point A
(positive CW).
∆Lsys A =
∑M
A ∆t
→
(IG ω′ + mv′G r ) − (IG ω + mvG (0.18 − 0.02)) = 0
(1)
Note that the moment arm for mv G is just the vertical distance between the line of action of mv G and point A. We have one equation
and four unknowns ( ω′, v ′G , ω, v G ). To get another equation we will use kinematics. Before the impact the ring is rolling without
slipping and after the impact we have fixed axis rotation giving
v ′G = ω′r
(2)
v G = ωr
(3)
We still need one more equation. For the final motion of the disk we can use
conservation of energy. Our two locations will be immediately after the impact and
when it has reached the top of the step as shown in the figure. Since the contact
force will do no work we get
Position 1
E sys1 = E sys2
or
E k 1 + E g1 = E k 2 + E g 2
where
Position 2
(4)
datum
4–37
1
1
m(v ′G )2 + I G (ω′)2
2
2
=0
E k1 =
E g1
E k2 = 0
E g 2 = mg(0.02)
We can solve these 4 equations and 4 unknowns as shown below.
So the smallest angular velocity the ring can have so that it makes it over the step is 2.61 rad/s (CW).
Example 4/17
A slender bar 1.5 meters long and weighing 10 kg is dropped onto a horizontal surface as shown.
Assume the friction between the bar and the ground is large. Immediately after the impact:
a) Determine the angular velocity of the bar for e = 0.5
b) Plot the angular velocity as a function of the coefficient of restitution for e = 0 to e = 1.
b) How does your answer change if the surface is frictionless?
G
70°
0.8 m
Strategy: We really have two things going on here. First, the bar falls and second, we have an impact. For the bar dropping we can use
conservation of energy, and for the impact we will use the finite time forms of LM and AM. We will pick the bar as our system when
using these principles. Since we are given a coefficient of restitution, we will also need to use the coefficient of restitution equation.
Falling: The two positions are shown in the figure below. Conservation of energy for a closed
system is
Position 1
G
E sys2 − E sys1 = W
0.8 m
Position 2
Datum
4–38
Since we have no work being done in this problem and the bar does not rotate on the way down, we get the energy at position one is
equal to the energy at position two, that is,
E sys1 = E sys 2
mgh =
1
mv 2
→ v = 2gh = 2(9.81m/s 2 )(0.8 m) = 3.96 m/s = v G1 (velocity before the impact)
2
Impact: Let’s draw impulse-momentum diagrams for the bar as shown below. Our two times are immediately before the impact and
immediately after the impact. Since it is not obvious what the direction of the center of gravity will be after impact (it is not fixed axis
rotation), we will just put a general x and y component.
G
mv ′G x
70°
I G ω′
-
=
G
mv G1
mv ′G y
70° Px∆t
70°
P
P
P
G
Py∆t
Using these diagrams, we can get three equations: Linear momentum in the x-direction and in the y-direction and angular momentum
about any point. Since we are not interested in determining the impulse that acts at point P let’s just use AM about point P and not
bother with the linear momentum equations. Angular momentum about P (positive CW)
L
L
L
I G ω′ + mv′G y cos 70° + mv′G x sin 70° − (mv G 1 )( cos 70°) = 0
2
2
2
(1)
We have three unknowns in this equation, ( ω′, v ′G x , v ′G y ). We can find IG for a slender bar using
IG =
1
1
mL2 = (10 kg)(1.5 m) 2 = 1.875 kg − m 2 .
12
12
We still need more two equations. Let’s use the coefficient of restitution equation. We will start by writing it down in generic terms and
then apply it to our specific problem
(
v ′PB n − v ′PA n = e v PA n − v PB n
)
For our problem let’s define the ground to be object A and we will drop the subscript for B. The point of contact is
point P and I will define the normal direction positive up as shown. I will also assume that point P will have a
normal velocity up after the impact. Therefore, we get:
(
v ′Pn − 0 = e 0 − (− v Pn )
)
n
G
The speed of point P in the normal direction before the impact will simply be the velocity of the center of the bar
(it is translating) so v Pn = v G1 and we get
v ′Pn = ev G1
(2)
One of the most common mistakes is to get one of the signs wrong in this equation. We now have 2 equations and 4 unknowns
( ω′, v ′G x , v ′G y , v ′Pn ). Where do we look for more equations? Kinematics! Let’s relate the velocities of point G and point P. How do
4–39
we do this? Can we find the instantaneous center for the bar? It is not very easy to do that in this case, so we will just use the vector
equation that is used to relate the velocity of two points on the same rigid body, that is
r r
r
r
v P = v G + ω × rP / G
Since we are assuming the friction is large, the point of contact, P, will only have a velocity in the normal direction. Substituting in the
variables we defined for points P and G after the impact we get
r r
r
r
v ′P = v ′G + ω′ × rP / G
(
(
)
)
L
L
v ′Pn ˆj = v ′G x ˆi − v ′G y ˆj + (−ω′kˆ ) × − cos 70°ˆi − sin 70°ˆj
2
2
L
L
= v ′G x ˆi − v ′G y ˆj + ω′ cos 70°ˆj − ω′ sin 70°ˆi
2
2
Equating components we get
ˆi :
ˆj :
0 = v ′G x − ω′
L
sin 70°
2
v ′Pn = − v ′G y + ω′
L
cos 70°
2
(3)
(4)
We now have four equations and four unknowns that we can solve. Since for part b) we want to plot the angular velocity as a function
of e, we will use Maple to solve for our answers in terms of e.
> m:=10:
L:=1.5:
g:=9.81:
h:=0.8:
IG:=1/12*m*L^2;
thR:=70*Pi/180;
Velocity of impact
> vG1:=sqrt(2*g*h);
IG := 1.875000000
7π
thR :=
18
vG1 := 3.961817765
Impact problem
> eq1:=IG*omegap+m*vGyp*L/2*cos(thR)+m*vGxp*L/2*sin(thR)+m*vG1*L/2*cos(thR);
eq2:=vPnp=e*vG1;
eq3:=0=vGxp-omegap*L/2*sin(thR);
eq4:=vPnp=-vGyp+omegap*L/2*cos(thR);
eq1 := 1.8750 omegap + 2.5652 vGyp + 7.0477 vGxp − 10.163
eq2 := vPnp = 3.961817765e
7π
eq3 := 0 = vGxp − 0.7500000000omegap sin
18
7π
eq4 := vPnp = −vGyp + 0.7500000000omegap cos
18
> evalf(solve({eq1,eq2,eq3,eq4},{omegap,vGyp,vGxp,vPnp}),4);
{ vGyp = −3.614 e + 0.3476, vPnp = 3.962 e, omegap = 1.355 e + 1.355, vGxp = 0.9550 e + 0.9550}
For part a) we were told e = 0.5, so
4–40
ω′ = 1.355(0.5) + 1.355
= 2.03 rad/s (clockwise)
We have already solved part b) since we found the angular velocity as a function of the coefficient of restitution
ω′ = 1.355e + 1.355
A plot of this relationship is shown below
For part c) we were asked how our answer would change if the surface were frictionless. Our impulse-momentum diagrams would be
the same except that there would be no impulse in the x-direction and the velocity of the point of contact, P, could have a velocity
component in the x-direction. Therefore, we would have
AM about point P (same as before)
L
L
L
I G ω′ + mv′G y cos 70° + mv′G x sin 70° − (mv G 1 )( cos 70°) = 0
2
2
2
(1c)
Coefficient of restitution (same as before)
v ′Pn = ev G1
(2c)
Kinematics relating G and P (not quite the same as before)
r r
r
r
v ′P = v ′G + ω′ × rP / G
(
(
)
)
L
L
v ′Px ˆi + v ′Pn ˆj = v ′G x ˆi − v ′G y ˆj + (−ω′kˆ ) × − cos 70°ˆi − sin 70°ˆj
2
2
L
L
= v ′G x ˆi − v ′G y ˆj + ω′ cos 70°ˆj − ω′ sin 70°ˆi
2
2
Equating components we get
ˆi :
ˆj :
v ′Px = v ′G x − ω′
L
sin 70°
2
(3c)
v ′Pn = − v ′G y + ω′
L
cos 70°
2
(4c)
So we now have 4 equations (1c-4c) and 5 unknowns ( ω′, v ′G x , v ′G y , v ′Pn , v ′Px ). Where do we get another equation? Remember, we
had the two conservation of linear momentum equations we didn’t apply because we weren’t interested in Px∆t and Py∆t. In part c) we
know that Px∆t is zero, so let’s use LM in the x direction.
Linear momentum in the x-direction (+ →):
mv G x − 0 = 0
(5c)
We now have 5 equations and 5 unknowns which we can solve. The final answer for the angular velocity from Maple is shown below.
ω′ = 4.012e + 4.012
4–41
4.4.3 Accelerations
In the previous section we solved a large variety of problems simply knowing how
to relate the velocity of several points on a rigid body. We used conservation of
energy and conservation of linear momentum/angular momentum finite time. We
were able to do this since both of these principles only involve velocities. The type
of problem we have not yet solved are those that involve rigid bodies undergoing
general plane motion where we need to use conservation of linear
momentum/angular momentum rate form. This is because we need the acceleration
of the center of gravity and we have not discussed how to determine this yet.
We know from the previous section that general plane motion can be thought of as
a translation plus a fixed axis rotation. We said that we could relate the velocity of
two points on the same rigid body using
r
r
r
vB = vA + vB / A
(4.11)
r r
r
= v A + ω × rB / A
To get the acceleration we simply need to differentiate
r
r
dv
dv
r
r
r
a B = A + B/ A = a A + a B/ A
dt
dt
r r
d (ω × rB / A )
r
= aA +
dt
r
r
r r
r dr
= a A + α × rB / A + ω × B / A
dt
r
r r
r r r
= a A + α × rB / A + ω × (ω × rB / A )
r
r r
r
= a A + α × rB / A − ω 2 rB / A (plane motion)
In summary, to relate the acceleration of two points on the same rigid body we use
r
r
r r
r
r r
a B = a A + α × rB / A + ω × (ω × rB / A )
Note: Key Equation
(4.12)
or if we have plane motion this simplifies to
r
r
r r
r
a B = a A + α × rB / A − ω 2 rB / A (plane motion)
(4.13)
r r r
r
Warning: Derivation of ω × (ω × rB / A ) = −ω2 rB / A
r
r
If the body is undergoing plane motion we know ω = ωkˆ and rB / A = xˆi + yˆj . If
r
r r
we substitute these into ω × (ω × rB / A ) we get
r r r
ω × (ω × r
) = ωkˆ × (ωkˆ × ( xˆi + yˆj))
B/ A
= ωkˆ × (ωxˆj − ωyˆi )
= −ω 2 xˆi − ω 2 yj
= −ω 2 ( xˆi + yˆj)
r
= −ω 2 rB / A
End of Derivation
4–42
Observations:
r
• a B / A has a normal and a tangential component
r r
• Tangential component = α × rB / A
o Magnitude = αrB / A
o Direction = perpendicular to rB / A
r
r r
• Normal component = ω × (ω × rB / A )
o
•
Magnitude = ω2 rB / A
o Direction = towards point A
When solving problems I would suggest using the vector algebra
approach.
Figure 4.16 is a pictorial illustration of this equation relating the acceleration of two
points on the same rigid body.
B
aA
B
aB
=
A
aA
General Plane Motion
r
aB
+
A
=
=
aB/At
B
aB/An
A
aA
Translation
r
aA
+
+
Fixed Axis Rotation
r r
r r r
α × rB / A + ω × (ω × rB / A )
Figure 4.16 - Illustration of terms in the equation relating the acceleration of two
points on a rigid body
A
A
A
aA
aA
When solving problems
• Pinned joints: The point where the pin is located has the same velocity and
acceleration regardless of which body you isolate as your system as shown
in Fig. 4.17.
• Gears: The tangential components of acceleration of the two objects are the
same, but the normal acceleration will be different as shown in Fig. 4.18.
Figure 4.17 - Pin joints
A
Figure 4.18 - Gears or rolling
without slip contact
Rolling motion (for an object that has a radius r and a center of gravity located at
the geometric center): A generic KD and FBD are shown in Fig. 4.19 for an object
that is rolling or rotating and sliding on a horizontal surface. If the object is rolling,
there is a kinematic relationship between the acceleration of the center of gravity
and the angular acceleration, but the friction force is unknown (you do know it has
to be less than µsN) as shown in Table 4.4. If the object is sliding, then the friction
force is known, but there is no kinematic relationship between the acceleration of
the center of gravity and the angular acceleration.
KD
FBD
I Gα
maG
F
N
Figure 4.19 - Generic free body diagram and kinetic diagram
for a round object moving on a horizontal surface
4–43
Table 4.4 - Friction forces and kinematic relationships for an object that is rolling or
rotating and sliding
Case
Kinematic Relationship
(mass center=geometric center)
Friction Force
Rolling, no sliding:
aG = αr
F is unknown
(but it is < µsN)
Rolling, sliding impending:
aG = αr
F = µsN
Rotating and sliding:
aG = ?, α = ?
(aG ≠ αr)
F = µkN
Warning: Derivation of kinematic relationship aG = αr
Let’s derive the relationship between the acceleration of the center of gravity of an
object that is rolling (which means no slipping) on a fixed surface as shown in
Figure 4.20.
α
ˆj
G
r
ˆi
C
Figure 4.20 - Rolling without slip
Method 1: Use a vector algebra equation relating the acceleration of point C and
the center of gravity G.
Since the object is undergoing plane motion we know
r
r
r r
r
a G = a C + α × rG / C − ω2 rG / C
So, what do we know in this equation? We know
r
•
α = −αkˆ (found using the right hand rule)
r
•
rG / C = rˆj
r
• Since G is traveling in a straight line, a G is in the x direction, that is,
r
a = a ˆi
G
•
G
Since C is in contact with the ground (and the ground has zero
acceleration) the acceleration of C will only be in the y-direction, that is,
r
a = a ˆj
C
C
When we substitute this in we get
a G ˆi = a C ˆj + (−αkˆ ) × rˆj − ω2 rˆj
= a ˆj + αrˆi − ω2 rˆj
C
Equating components we get:
ˆi :
ˆj :
a G = αr
0 = a C − ω2 r
→ a C = ω2 r
4–44
Therefore, the acceleration of the center of gravity is a G = αr (which is what we
wanted to show) and the acceleration of the point of the object in contact with the
ground is a C = ω2 r directed upwards.
Method 2: The second method we will use to illustrate that a G = αr (in the case of
the mass center being at the geometric center) is more intuitive. If we know that
the object does not slip then the distance the center of gravity will move after the
object rolls through an angle θ is simply the arc length. That is
x G = rθ
If we differentiate this (and recognize that r does not depend on time) we get
v G = rω
and
a G = rα
End of Derivation
Example 4/18
A bowling ball with radius 4.3 in. has a radius of gyration about its center of gravity of 3.28 in. If the ball is released with a velocity of
20 ft/s but with no angular velocity as it touches the alley floor, compute the time before the ball begins to roll without slipping. The
coefficient of friction between the ball and the floor is 0.2.
v0
v
ω=0
Strategy: We have two choices (we’ll do it both ways): 1) Linear and angular momentum (rate form) or 2) linear and angular
momentum (finite time form). Remember that when you are given the radius of gyration, kG, the mass moment of inertia is
I G = mk G2 . For the system we will use the bowling ball.
Linear and Angular Momentum (rate)
As usual when we apply this we need a KD and a FBD. The ball will be sliding initially, so we know the friction force which we will
put directly on the FBD.
KD
FBD
I Gα
mg
maG
µkN
N
4–45
r
dPy
LM y-direction (+↑)
dt
=
∑F
→
y
r
dPx
LM x-direction (+ →)
=
dt
r
dL G
AM about G (positive CW)
=
dt
∑F
→
x
∑M
0 = N − mg
G
→ N = mg
(1)
ma G = −µ k N = −µ k mg
→
(2)
I g α = −µ k Nr
→ mk G2 α = −µ k mgr
Solving Eq. 2 for the acceleration of the center of gravity, we get a G = −µ k g and Eq. 3 for the angular acceleration we get α =
(3)
µ k gr
.
k G2
Therefore, using LM and AM rate, we found that the acceleration of the center of gravity and the angular acceleration are both constants.
The question is therefore when will the ball stop sliding and start rolling without slipping? This will occur when the velocity of the
point of contact is zero, or alternatively, when the velocity of the center of gravity, vG = ωr. To find equations for the velocity we need
to use our kinematic relationships and integrate, which in this case will just give us the standard constant acceleration equations. That is,
vG = vG o + a G t = vo − µ k gt
ω = ω o + αt = 0 +
µ k gr
k G2
(4)
t
(5)
Setting vG = ωr we get
v o − µ k gt =
µ k gr
k G2
rt
solve
fort → t =
vo
r
µ k g 1 + 2
k G
2
=
20 ft/s
(4.3 in) 2
(0.2)(32.2 ft/s 2 )1 +
(3.28 in) 2
t = 1.14 s
Linear and Angular Momentum (finite time)
When using this principle we draw impulse-momentum diagrams. Our two times are right after the ball is released and when the ball
starts rolling without slipping.
IGω2
mg∆t
mvo
mvG 2
µkN∆t
N∆t
Momentum after
time interval
Momentum before
time interval
Impulses during
time interval
0 − 0 = N∆t − mg∆t
(1a)
LM x-direction (+ →)
mvG 2 − mvo = −µ k N∆t
(2a)
AM about G (positive CW)
I G ω 2 − 0 = −µ k N∆tr
(3a)
LM y-direction (+↑)
4–46
In Eqs. 1a-3a we have 4 unknowns, N, ∆t , v G 2 , ω2 so we need one more equation. The last equation is the kinematic equation relating
v G 2 and ω2
vG 2 = ω2 r
(4a)
We can solve these equations in Maple and we get the same answer shown above.
Example 4/19
The velocity of point A is 10 in/s down the slot and its
acceleration is 100 in/s2 up the slot when in the position shown.
Determine the acceleration of point C.
C
B
9”
A
30°
12”
Strategy: Since we are given the velocity and the acceleration, this appears to be a pure kinematics problem and all we need to do is to
use the equations for relating the velocity of two points on the same rigid body. Note: we almost always need to solve the velocity
problem before we solve the acceleration problem.
Velocity
We have two choices to determine the angular velocity of the bar (we need the angular velocity because our acceleration equation has an
ωx(ωxr) term). We’ll do it both ways.
vC
Method 1 - Instantaneous center of velocity. We know the velocity
of A is down the slot and the velocity of C is up or down due to the
vertical slot. Therefore, we can find the IC as shown in the figure.
B
C
IC
From geometry we can find
rA/IC = 9 / cos(30°) = 10.39 in/s
9”
rC/IC = 12 − 9 tan (30°) = 6.80 in/s
30°
A
10 in/s
So
v A = ωrA / IC
→ ω =
vA
10 in/s
=
= 0.962 rad/s
rA/IC 10.39 in
12”
Now that we have the angular velocity, we can do the acceleration problems. Remember we cannot use the IC for accelerations since
the acceleration of the IC is not zero. Before we move on to the acceleration problem, let’s find the angular velocity using the second
method you are familiar with, that is, the vector algebra approach.
Method 2 - Vector algebra. The vector equation relating the velocities of points A and C is
r r
r
r
v C = v A + ω × rC / A
r
Using the standard coordinate system shown to the right and substituting in what we know (assume ω = ωkˆ ) we get
ˆj
ˆi
4–47
v C ˆj = (10 cos(30°))ˆi −(10sin (30°))ˆj + ωkˆ × (12ˆi + 9ˆj)
= 8.66ˆi − 5ˆj + 12ωˆj − 9ωˆi
Equating components gives:
ˆi : 0 = 8.66 - 9ω
→
ω = 0.962 rad/s
ˆj : v = -5 + 12ω = -5 + 12(.0962)
→ v C = 6.54 in/s
C
Now let’s do the acceleration problem using the vector algebra approach.
Acceleration
r
r
r r
r
a C = a A + α × rC / A − ω 2 rC / A
Substituting into this equation we get
a C ˆj = (−100 cos 30ˆi + 100 sin 30ˆj) + αkˆ × (12ˆi + 9ˆj) − (0.962) 2 (12ˆi + 9ˆj)
= - 86.6ˆi + 50ˆj + 12αˆj - 9αˆi - 11.1ˆi - 8.33ˆj
Equating components gives:
ˆi : 0 = -86.6 - 9α - 11.1
→
r
α = -10.8 rad/s2 or α = -10.8 rad/s2 kˆ
r
2
2
ˆj : a = 50 + 12α - 8.33
→ a C = −88.46 in/s or a C = 88.46 in/s ↓
C
Example 4/20
1 ft
Bar CD rotates with a constant angular velocity of 10 rad/s
counterclockwise. Determine the angular velocity and angular
acceleration of bars AB and BC at the instant shown.
A
B
30o
2f
t
45o
D
C
0.4 ft
Strategy: This is a pure kinematics problem. We should start with the bar we know something about, bar CD and then move on to the
other bars.
For these types of problems, it is always easiest to start with the velocity problem. Bar CD is undergoing fixed axis rotation, so the
velocity of C can be found using vector algebra or by recognizing that the magnitude of the velocity is simply v C = ω CD rCD and its
direction is perpendicular to bar CD. Therefore
v C = ω CD rCD = (10 rad/s)(0.4 2 ft ) = 4 2 ft/s at 45° down from horizontal.
To confirm that we can also do this using vector algebra
r
r
r
v C = ω CD × rC / D
= 10kˆ × (−0.4ˆi − 0.4ˆj)
= −4ˆj + 4ˆi
ft/s
4–48
This is the same answer we found using the scalar approach. Now moving on to bar BC we have the same choice, do we use
instantaneous center of velocity or vector algebra? The geometry is really not that bad, so using the instantaneous center of velocity is
probably not very difficult, but let’s use vector algebra since it is so systematic.
Relating the velocity of point B to point C on bar BC we get:
r
r
r
r
v B = v C + ω BC × rB / C
Substituting in what we know and don’t know we get
v B x ˆi + v B y ˆj = (4ˆi − 4ˆj) + ω BC kˆ × (−2 cos 30°ˆi + 2 sin 30°ˆj)
= 4ˆi − 4ˆj − 1.732ω BC ˆj − ω BC ˆi
Equating components we get:
ˆi :
v B x = 4 − ω BC
ˆj :
v B y = −4 − 1.732ω BC
(1)
(2)
We have 2 equations and 3 unknowns ( v B x , v B y , ω BC ). Moving to bar AB we get
r
r
r
r
v B = v A + ω AB × rB / A
Substituting in what we know we get
v B x ˆi + v B y ˆj = 0 + ω AB kˆ × (−1ˆi )
= −1ω AB ˆj
Equating components we get:
ˆi :
v Bx = 0
(3)
ˆj :
v B y = −ω AB
(4)
We now have 4 equations and 4 unknowns that we can solve. If we are solving the equations by hand it is probably easiest to go ahead
and solve for the unknown angular velocities at this point, but since we will use Maple, we might as well find the equations necessary to
determine the angular accelerations of BC and AB as well. Starting with bar BC, we can find the acceleration of point C since point C
2
is undergoing fixed axis rotation. It will have a normal component directed towards D equal to ω CD
rC / D and a tangential component
equal to zero since CD is rotating at a constant angular velocity. Therefore,
r
a C = (10 rad/s) 2 (0.4 2 ft) = 40 2 ft/s 2 at 45° up from horizontal.
We could also have obtained this result using vector algebra
r
r
r
2 r
a C = α CD × rC / D − ω CD
rC / D
r
2
= 0 − (10) (−0.4 i − 0.4ˆj)
r
= 40 i + 40ˆj ft/s 2
Relating the velocity of point B to point C on bar BC we get:
r
r
r
r
r
a B = a C + α BC × rB / C − ω 2BC rB / C
4–49
Substituting we get
a B x ˆi + a B y ˆj = (40ˆi + 40ˆj) + α BC kˆ × (−2 cos 30°ˆi + 2 sin 30°ˆj) − ω 2BC (−2 cos 30°ˆi + 2 sin 30°ˆj)
= 40ˆi + 40ˆj − 1.732α BC ˆj − α BC ˆi + 1.732ω 2BC ˆi − ω 2BC ˆj
Equating components we get:
ˆi :
a B x = 40 − α BC + 1.732ω 2BC
(5)
ˆj :
a B y = 40 − 1.732α BC − ω 2BC
(6)
We have 6 equations and 7 unknowns ( v B x , v B y , ω BC , ω AB , a B x , a B y , α BC ). Moving to bar AB we get
r
r
r
r
r
a B = a A + α AB × rB / A − ω 2AB rA / B
Substituting we get
a B x ˆi + a B y ˆj = 0 + α AB kˆ × (−1ˆi ) − ω 2AB (−1ˆi )
= −1α AB ˆj + ω 2AB ˆi
Equating components we get:
ˆi :
a B x = ω 2AB
(7)
ˆj :
a B y = −α AB
(8)
We now have 8 equations and 8 unknowns ( v B x , v B y , ω BC , ω AB , a B x , a B y , α BC , α AB ) that we can solve in Maple.
We could have used Maple to do all the cross products if we had wanted to. In this case, we would have had the six vector equations:
r
r
r
r
r
r
r
Velocity of B from bar BC: v B = v C + ω BC × rB / C
r
r
r
r
Velocity of B from bar AB: v B = v A + ω AB × rB / A
r
r
r
2 r
Acceleration of C from bar CD: a C = α CD × rC / D − ω CD rC / D
r
r
r
r
2 r
Acceleration of B from bar BC: a B = a C + α BC × rB / C − ω BC rB / C
r
r
r
r
r
Acceleration of B from bar AB: a B = a A + α AB × rB / A − ω 2AB rA / B
Velocity of C from bar CD: v C = ω CD × rC / D
These equations will give us 12 scalar equations for plane motion. The Maple code to implement these vector equations and to solve the
resulting equations is shown below. There may be a better way of doing this in Maple, but this was the first way I got it to work, so I’m
sticking with it! I have tried to include enough comments that the code is fairly self explanatory (if you know Maple that is),
4–50
Load the linear algebra package, insert a : to inhibit output
> with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
Define the known quantities:
> omegaCD:=[0,0,10]:
> alphaCD:=[0,0,0]:
> rC_D:=[-0.4,-0.4,0]:
> rB_C:=[-2*cos(30*Pi/180),2*sin(30*Pi/180),0]:
> rB_A:=[-1,0,0]:
Define the unknown quantities:
> VC:=[vCx,vCy,0]:
> VB:=[vBx,vBy,0]:
> omegaBC:=[0,0,wBC]:
> omegaAB:=[0,0,wAB]:
> AC:=[aCx,aCy,0]:
> AB:=[aBx,aBy,0]:
> alphaBC:=[0,0,aBC]:
> alphaAB:=[0,0,aAB]:
Write the governing equation but move all the terms
to the same side of the equation.
> eq1:=evalm(crossprod(omegaCD,rC_D)-VC);
> eq2:=evalm(VC+crossprod(omegaBC,rB_C)-VB);
> eq3:=evalm(crossprod(omegaAB,rB_A)-VB);
> eq4:=evalm(crossprod(alphaCD,rC_D)+crossprod(omegaCD,crossprod(omegaCD,rC_D))-AC);
> eq5:=evalm(AC+crossprod(alphaBC,rB_C)+crossprod(omegaBC,crossprod(omegaBC,rB_C))-AB);
> eq6:=evalm(crossprod(alphaAB,rB_A)+crossprod(omegaAB,crossprod(omegaAB,rB_A))-AB);
eq1 := [ 4.0 − vCx, −4.0 − vCy, 0. ]
eq2 := [ −vBx + vCx − wBC , −vBy + vCy − wBC 3 , 0 ]
eq3 := [ −vBx, −wAB − vBy, 0 ]
eq4 := [ 40.0 − aCx, 40.0 − aCy, 0. ]
eq5 := [ −aBx + aCx − aBC + wBC 2 3 , −aBy + aCy − aBC 3 − wBC 2, 0 ]
eq6 := [ wAB2 − aBx, −aAB − aBy, 0 ]
Form the scalar equations
>eqns1:={seq(eq1[k],k=1..2),seq(eq2[k],k=1..2),seq(eq3[k],k=1..2),seq(eq4[k],k=1..2),seq(eq
5[k],k=1..2),seq(eq6[k],k=1..2)};
eqns1 := { 40.0 − aCx, −vBx, −aBy + aCy − aBC 3 − wBC 2, −aBx + aCx − aBC + wBC 2 3 , −4.0 − vCy,
4.0 − vCx, wAB2 − aBx, −wAB − vBy, −aAB − aBy, 40.0 − aCy, −vBy + vCy − wBC 3 , −vBx + vCx − wBC
}
Solve the equations
> sol:=evalf(solve(eqns1),4);
sol := { wBC = 4., aBy = 113.6, aBC = -51.71, aBx = 119.4, aAB = -113.6, vCx = 4., vCy = -4., vBx = 0.,
aCy = 40., wAB = 10.93, vBy = -10.93, aCx = 40. }
What could I have done to make this problem more difficult? Not much really. If I had given you a different orientation then the
geometry may have been more difficult, but other than that, the equation will stay the same. What if I had asked you to look at the full
range of motion, for example, to plot the acceleration of point B as a function of the crank angle, θ, that is, the angle of bar CD? It’s the
same problem! The only difficulty is that you need to express all of your position vectors in term of θ and then solve for your final
answers in terms of θ. By hand this would likely be a pain, but in Maple it is not too difficult.
4–51
Example 4/21
A stepped disk that weighs 40 lbf (m=1.24 slugs) and has a
mass moment of inertia of 0.2 slug-ft2 has a cable wrapped around
it as shown. If it is released from rest, determine
a) the initial acceleration of the center of gravity
b) the tension in the cable
c) how long would it take to fall 3 ft?
ri = 4"
rO = 8"
Strategy: We need to use LM and AM rate since we are interested in accelerations. To find how long it will take to fall three feet we’ll
need to use kinematics (after we find the acceleration).
FBD
KD
We will start by drawing a FBD and KD as shown.
T
LM y-direction (+ ↓)
r
dPy
dt
=
∑F
y
→
ma G = mg - T
(1)
I G α = Tri
(2)
I Gα
AM about G (positive CW)
r
dL G
=
dt
∑
maG
MG
→
mg
where ri = 0.333 ft. We have 3 unknowns in these two equations: aG, T, α. Our final equation will be the kinematic relationship
aG = αri
2
(3)
2
Solving these three equations we get α = 39.5 rad/s , aG = 13.16 ft/s , and T = 23.7 lbf. To find the distance the disk will travel we
simply integrate the acceleration (or use the traditional constant acceleration equations since aG is constant) to get
x=
1
aGt2
2
solve
fort →
t = 0.675 s
4–52
Example 4/22
A uniform slender bar AB of mass mb is suspended as shown
from a uniform disk of mass md. Assuming the disk rolls
without slipping determine the equations necessary to determine
the acceleration of point A and the angular acceleration of the bar.
DO NOT SOLVE THE EQUATIONS. Your answer should consist
of a set of numbered equations and a list of unknowns.
r
No slipping
A
L
P
B
Strategy: Since we are asked to find accelerations, we are naturally led to apply LM and AM rate.
As a system we will start by looking at the disk. A FBD and KD are shown below.
KD
LM x-direction (+ ←)
r
dPx
=
dt
∑
Fx
→
mDa A = F − A x
FBD
Ay
I GD α D
(1)
Ax
mDa A
mDg
LM y-direction (+↑)
r
dPy
=
dt
∑F
y
→
0 = N − mDg + A y
F
(2)
N
AM about G (positive CCW)
r
dL G
=
dt
∑M
g
→
I G D α D = −Fr
(3)
1
m D r 2 . We have six unknowns ( F, A x , A y , N, a A , α D ) in these 3 equations so we
2
1
need more equations. Let’s start by picking a new system, the bar. We will denote the mass of the bar as mB and I G B =
m B L2 .
12
where mD is the mass of the disk and I G D =
LM x-direction (+→)
r
dPx
=
dt
∑F
x
→
Ax
m B a G x = −A x
(4)
I Gb α b
LM y-direction (+↑)
r
dPy
dt
=
∑
Fy
→
m B a G y = −A y − m B g
m ba Gy
m b a Gx
(5)
Ay
mbg
AM about G (positive CCW)
r
dL G
=
dt
∑M
G
→
I GB α B = A x
L
2
(6)
We now have 6 equations and 9 unknowns. Where do we look for more equations? Kinematics. Since we are told the disk rolls
without slipping we know
aA = αDr
(7)
4–53
We can also relate the acceleration of the center of gravity of the bar to that of the disk.
r
r
r
r
r
a A = a G + α B × rA / G − ω 2B rA / G
0 (starts from rest)
Substituting in what we know we get
− a A ˆi = a G x ˆi + a G y ˆj + α B kˆ ×
= a G x ˆi + a G y ˆj − α B
Lˆ
j− 0
2
Lˆ
i
2
Equating components we get:
ˆi :
ˆj :
- a A = a Gx − α b
L
2
(8)
0 = a Gy
(9)
We now have 9 equations and 9 unknowns that can be solved.
Example 4/23
In an investigation of whiplash resulting from rear end collisions, rotation of the head is
of primary interest. The center of gravity of the head, G, is assumed to be a distance r
from the pivot point of the head, point O, and the head is assumed to have a centroidal
radius of gyration of kG. If point O is given a constant acceleration aO in the direction
shown, with the head initially at rest, determine the angular velocity of the head as a
function of the rotation angle, θ. Assume that the neck is relaxed so no moment is
applied to the neck at O.
θ
Vertical
G
r
O
aO
Strategy: You might be tempted to use conservation of energy because we have two positions. Position 1 is when the head is vertical
and position 2 is when the head has rotated through an angle θ. The problem with this strategy is that point O will also be moving
during this process and we don’t know how far, so we will not be able to determine the work of the external forces at that point.
Therefore, since we are given the acceleration of point O, let’s use the rate form of conservation of linear and angular momentum
(Newton’s 2nd Law).
As a system we will choose the head. When we apply Newton’s 2nd Law, we always start with a FBD and a KD. One of the key steps
in drawing these diagrams is to place the head at some arbitrary angle, θ, as shown.
ma G y
KD
FBD
y
IGα
Oy
x
r
ma G x
θ
O
mg
θ
r
Ox
The head will be undergoing general plane motion since no point on it is fixed, which is why on our kinetic diagram I represented the
acceleration of the center of gravity as having a general x and y component.
4–54
Since the problem does not ask for the reactions at point O, and they will appear if we apply linear momentum in the x and y directions,
let’s just use conservation of angular momentum about point O.
Angular momentum about O (positive CCW)
dL sysO
dt
=
∑M
O
→ I G α − ma G x r cos θ − ma G y r sin θ = mgr sin θ
(1)
2
We have 3 unknowns in this equation ( a G x , a G y , α ) and one equation. The mass moment of inertia is I G = mk G
. Let’s use
kinematics to relate the acceleration of the center of gravity to the acceleration of point O. For plane motion we have
r
r
r
r
r r
r
a G = a O + a G / O = a O + α × rG / O − ω 2 rG / O
Substituting in the directions we have already assumed when we drew our kinetic diagram we get
a G x ˆi + a G y ˆj = a O ˆi + (αkˆ ) × (−r sin θˆi + r cos θˆj) − ω 2 (− r sin θˆi + r cos θˆj)
= a O ˆi − αr sin θˆj − αr cos θˆi + ω 2 r sin θˆi − ω 2 r cos θˆj)
Equating components we get
ˆi :
a G x = a O − αr cos θ + ω 2 r sin θ
(2)
ˆj :
a G y = −αr sin θ − ω 2 r cos θ
(3)
We now have 3 equations and 4 unknowns ( a G x , a G y , α, ω ), so we need one last equation. The final equation is the kinematic
relationship between α and ω.
α=
dω
dt
Let’s start by solving Eq. 1-3 for α in terms of θ and ω.
> IG:=m*kG^2;
IG := m kG2
> eq1:=IG*alpha-m*aGx*r*cos(theta)-m*aGy*r*sin(theta)=m*g*r*sin(theta);
eq2:=aGx=aO-alpha*r*cos(theta)+omega^2*r*sin(theta);
eq3:=aGy=-alpha*r*sin(theta)-omega^2*r*cos(theta);
eq1 := m kG2 α − m aGx r cos ( θ ) − m aGy r sin( θ ) = m g r sin( θ )
eq2 := aGx = aO − α r cos ( θ ) + ω 2 r sin( θ )
eq3 := aGy = −α r sin( θ ) − ω 2 r cos ( θ )
> simplify(solve({eq1,eq2,eq3},{aGx,aGy,alpha}));
r ( cos ( θ ) aO + g sin( θ ) )
{α =
,
kG2 + r2
aGx = −
aGy =
So
−aO kG2 − aO r2 + aO r2 cos ( θ )2 + r2 sin( θ ) cos ( θ ) g − r sin( θ ) ω 2 kG2 − r3 sin( θ ) ω 2
,
kG2 + r2
r ( −r sin( θ ) cos ( θ ) aO − r g + r g cos ( θ )2 − ω 2 cos ( θ ) kG2 − ω 2 cos ( θ ) r2 )
}
kG2 + r2
(4)
4–55
α=
r (a O cos θ + g sin θ)
k G2 + r 2
To get ω as a function of θ we need to separate variables and integrate using Eq. 4. Since we do not have α as a function of time we will
need to use the chain rule first,
dω dω dθ
dω r (a O cos θ + g sin θ)
=
=ω
=
dt
dt dθ
dθ
k G2 + r 2
α=
so
ω
∫
θ
ωdω =
∫
r (a O cos θ + g sin θ)
k G2 + r 2
0
0
dθ
1 2
r
ω = 2
(a O sin θ − g cos θ) oθ
2
2
kG + r
=
r
k G2
+ r2
(a O sin θ − g cos θ + g)
Solving for ω we get
2r
ω=
k G2
+ r2
(a O sin θ − g cos θ + g)
Let’s make some observations about this problem. When we solved Eq. 1-3 for α it turned out that ω didn’t enter the equation. Why is
that? It turns out there is an alternative way to draw our kinetic diagram in this problem that might make that clearer. You will recall on
our kinetic diagram we need to put the acceleration of the center of gravity. The way we initially solved the problem, we put an
unknown x and y component for this acceleration. Another option would be to look at our kinematic relationship before drawing our
kinetic diagram.
We know that the relationship between the acceleration of the center of gravity and point O is given by
r
r
r
r
r r
r
a G = a O + a G / O = a O + α × rG / O − ω 2 rG / O
so instead of putting the x and y components of the acceleration of G on the kinetic diagram, we could put the right hand side of this
equation because we know the direction of all of these terms as shown below.
Put these terms on the kinetic diagram
64
444447444444
8
r
r
r r
2r
a G = a O + α × rG / O −
ω rG / O
1
424
3
1
424
3
mag = αr
dir = ⊥ to r
Our FBD and KD are now
αr
mag = ω2 r
dir = pointing towards O
ω2r
KD
FBD
y
IGα
Oy
x
mαr
2
mω r
aO
maO
θ
O
mg
θ
r
Ox
It is clear from this kinetic diagram that when we take angular momentum about point O, the relative normal acceleration will not enter
the equation since it passes through point O. Angular momentum about O (positive CCW) for this FBD and KD is
4–56
dL sysO
dt
=
∑M
→ I G α + m(αr )r − ma O r cos θ = mgr sin θ
O
Substituting in for the mass moment of inertia and doing a little algebra we can immediately solve for α
(mk
2
G
)
+ mr 2 α = mgr sin θ + ma O r cos θ
→ α =
r (g sin θ + a O cos θ)
(k
2
G
+ r2
)
Which is the same answer we got before and the algebra was much easier. Which method is better? It doesn’t really matter. The first
one is a bit more methodic, but the second one is a bit more elegant.
4.5 Rotating Axis
In section 4.4 we discussed how to relate the velocity and acceleration of two
points on the same rigid body. Now, we will move on to describing the velocity
and acceleration of the same point, but described in two different coordinate
systems. For example, we are interested in the velocity and acceleration of a point
that is not attached to a rigid body, but has some sort of relative motion. For
example, point P in Figure 4.21 is free to move along the slot and is therefore not
attached to the rigid body. To solve this type of problem we will attach a
coordinate system to the body that can rotate with it. In this coordinate system the
relative motion is fairly easy to describe since it is just the motion along the slot.
All we need to know how to do is to relate the absolute time derivative of a vector
to the time derivative relative to the rotating frame and the rotation of the frame.
This turns out to be:
Where rotating axis
fits in the kinematics
concept map
r
r
r r
dQ ∂Q
=
+ ω× Q
dt ∂t
rel
rP/o
y
ω
Y ro
O
Angular velocity of the rotating frame
with respect to the fixed frame
Time derivative in
rotating frame
P
x
o
rP
X
Figure 4.21 Generic
situation where rotating
axis are required.
(4.14)
Time derivative in fixed
reference frame
This turns out to be a critical equation in kinematics and it is very useful when one
has a number of intermediate coordinate systems. Once again I will give the final
results and then show you how to use Eq. 4.14 to derive them afterwards. Eq. 4.15
gives the velocity of point P for the situation shown in Figure 4.21.
r r
r
r
r
v P = v o + v rel + ω × rP / o
where
r
v o = velocity of the origin of the rotating frame, oxyz
r
ω = angular velocity of the rotating frame measured in OXYZ
r
rP / o = position vector from point o to point P
r
v rel = relative velocity of point P with respect to point o
(4.15)
4–57
The acceleration of point P is
r
r
r
r r
r r r
r r
a P = a o + a rel + α × rP / o + ω × (ω × rP / o ) + 2ω × v rel
(4.16)
where
r
a o = acceleration of the origin of the rotating frame, oxyz
r
a rel = relative acceleration of point P with respect to point
o as measured by an observer attached to the rotating frame
r
α = angular acceleration of the rotating frame measured in OXYZ
r r
2ω × v rel = Coriolis acceleration
r r
r r r
α × rP / o + ω × (ω × rP / o ) = coincident acceleration
For plane motion Eq. 4.16 reduces to
r
r
r
r r
r
r r
a P = a o + a rel + α × rP / o − ω 2 rP / o + 2ω × v rel
(4.17)
The key step in using these equations is to clearly define your coordinate systems.
Derivation of Velocity and Acceleration Relationships using Eq. 4.14.
If we look at the generic problem shown in Figure 4.21 we have defined a fixed
coordinate system OXY and a rotating coordinate system oxy that is attached to the
body and therefore rotates with the body. The position vector from the origin of the
fixed coordinate system to point P is
r
r r
rP = ro + rP / o
r r
ω × rP / o
r
v rel
The velocity of point P is simply the time derivative of this with respect to the fixed
coordinate system
r r
r
d(r + r )
r
dr
= o P/o
v P = P
dt
dt OXY
OXY
r
r
d ro
d rP / o
=
+
dt OXY
dt OXY 142
4 43
4
r
d rP / o
dt
rp/o
y
ω
x
o
Y ro
rp
P
r
d rP / o
The quantity
dt
r r
+ ω× rP / o
oxy
r
r r
r
dr
= v o + P / o + ω × rP / o
dt
oxy
is the relative velocity of point P with respect to the
oxy
rotating axis so we will call it vrel resulting in the final equation for the velocity
O
X
Figure 4.22 Illustration of
terms in the velocity equation
r r
r
r
r
v p = v o + v rel + ω × rp / o
(4.15)
A vector diagram showing the last two terms in Eq. 4.15 is shown in Figure 4.22.
If we take the time derivative of Eq. 4.15 we get
4–58
r r
α × rP / o
y
ω
r r
2ω × v rel
r
a rel n
rp/o
x
o
Y ro
O
r
a rel t
P
r r r
ω × (ω × rP / o )
rp
X
Figure 4.23 Illustration of
terms in the acceleration
equation.
r
dv p
r
a P =
dt
r
dv
= o
dt
r
dv
= o
dt
r
dv
= o
dt
(
)
r r
r
r
d v o + v rel + ω × rp / o
=
dt
OXY
OXY
r r
r
d
(
r
ω
×
d
v
p/o )
+ rel
+
dt
OXY dt OXY
OXY
r
r
r r
r d rp / o
dv rel
+
+ α × rp / o + ω ×
dt OXY
dt OXY
OXY 142
43
142
4 r 43
4
r
r
dv rel
dt
r
v rel + ω× rP / o
r r
+ ωxv rel
oxy
r
r r
r r
r r
r r
dv
+ rel + ω × v rel + α × rp / o + ω × ( v rel + ω × rP / o )
dt
OXY
oxy
Taking the final cross product and collecting terms we have now derived Eq. 4.16.
(
)
r
r
r
r r
r r r
r r
a p = a o + a rel + α × rp / o + ω × ω × rp / o + 2ω × v rel
(4.16)
A vector diagram showing the last four terms in Eq. 4.16 is shown in Figure 4.23.
Note that the relative acceleration has two components, normal and tangential.
End of Derivation
The best way to understand these equations and how to apply them is through some
examples.
Example 4/24
The collar B is attached to the rod that is pinned at point A and
free to slide on the rod pinned at point D. At the instant shown,
the rod attached at A has an angular velocity of 5 rad/s (CCW) and an angular
acceleration of 2 rad/s2 (CW). Determine
a) the angular velocity of the rod attached at D
b) the angular acceleration of the rod attached at D.
200 mm
E
P
70°
B
D
25°
A
Strategy: We are given the angular velocity and acceleration of one link and want to calculate it for the other link, therefore this is a
pure kinematics problem. Also, since point P is not attached to link DE and there will be relative motion between point P and the link,
we will need to use our rotating axis equations.
Let’s start off by doing some geometry. The geometry, with all the known quantities, is shown in the figure to
the right. Using the law of sines we get
r
rAP
0.2
= DP =
sin 45° sin 25° sin 110°
rDP
D
45°
110°
rAP
0.2 m
25°
A
P
4–59
Solving we get rDP = 0.120 m and rAP = 0.266 m. At this point we are ready to define some coordinate systems. We will define a fixed
coordinate system at point A as shown below, and for link DE we have two choices. We can define a rotating coordinate system
attached to link DE as labeled “Option 1” or the one labeled “Option 2”.
y
E
P
Option 1
x
B
x
D
B
D
Option 2
rotating axis attached to DE
Y
Y
fixed axis
X
A
E
P
y
A
X
We will define the unit vectors in the X and Y directions to be ˆI and Jˆ respectively, and the unit vectors in the x and y to be ˆi and ˆj
respectively. We can solve the problem using the coordinates in either option 1 or option 2, so it really doesn’t matter which we choose.
We will use both just to illustrate the differences. If we are only interested in the answer at the instant shown, then option 1 is probably
the best choice since the unit vectors for the coordinates attached at A and D will be in the same orientation. The rotating axis given by
option 2 is convenient since the relative motion will always be in the x direction, but we will need to do a coordinate transformation to
solve the problem since ˆi and ˆj are not in the same direction as ˆI and Jˆ .
Option 1 (velocity)
We will start by finding the velocity of point P by looking at bar AP. Point P is attached to this bar and since it is undergoing fixed axis
rotation we know
r
r
r
v P = ω AP × rP / A
ˆ × (0.266 sin 25°ˆI + 0.266 cos 25°Jˆ )
= 5K
(1)
= 0.562Jˆ − 1.205ˆI m/s
We can now find the velocity of point P using the axis attached at point D. Since point P is not attached to body DE we need to use a
rotating axis. The velocity is
r
r
r
r
r
v P = v D + ω DE × rP / D + v rel
(2)
We know the velocity of point D is zero since it is a fixed pin and we also know that the relative velocity must be along the bar. The
best way to get the direction of the relative velocity is to ask yourself “If I were on object DE and was looking at point P, what direction
would it move?” Now, I recognize that some of you have zero visualization ability, but you really must work on this. Another question
you can ask yourself is “If I stop the rotation of the axis, that is, if bar DE were completely fixed in space, then what direction would
point P move?” It would have to move along the bar, so that is the direction of the relative velocity. Therefore we know the direction of
the relative velocity but not the magnitude. We also know the direction of the angular velocity of DE (in or out of the paper).
Substituting what we know into Eq. 2 we get
r
v P = 0 + ω DE kˆ × (0.120 sin 70°ˆi + 0.120 cos 70°ˆj) + ( v rel sin 70°ˆi + v rel cos 70°ˆj)
= 0.113ω ˆj − 0.041ω ˆi + 0.940 v ˆi + 0.342 v ˆj
DE
DE
rel
(3)
rel
Since we chose our coordinate systems in Option 1 so that they line up with each other, we can simply set Eq. 1 equal to Eq. 2 and
equate components.
ˆI (or ˆi ) :
−1.205 = −0.041ω DE + 0.940 v rel
(4)
4–60
Jˆ (or ˆj) :
0.562 = 0.113ω DE + 0.342 v rel
(5)
Solving Eq. 4 and Eq. 5 we get vrel = -0.941 m/s and ωDE = 7.82 rad/s.
Option 2 (velocity)
Let’s resolve the velocity problem using the axis defined in Option 2, that is, when the x-axis is directed along bar DE. The velocity of
point P is still given by Eq. 1 and Eq. 2. The difference arises when we substitute into Eq. 2 as shown below.
r
v P = 0 + ω DE kˆ × (0.120ˆi ) + v rel ˆi
= 0.120ω ˆj + v ˆi
DE
(6)
rel
The problem is that ˆi and ˆj are not in the same direction as ˆI and Jˆ so we need to relate them. Since this is a common problem, let’s
ˆ ) in the XY frame
take a short diversion to discuss how to relate vectors expressed in different coordinate systems, in this case ( ˆI, Jˆ, K
ˆ and
and ( ˆi , ˆj, kˆ ) in the xy frame. We just do the transformation for planar motion, that is when K
kˆ are in the same direction. Suppose we have the XY frame unit vectors ˆI and Jˆ as shown and the
xy frame unit vectors ˆi and ˆj rotated an angle θ in a counterclockwise direction. By inspection
ˆj
Jˆ
ˆi
θ
θ
ˆi = cos θˆI + sin θJˆ
ˆj = − sin θˆI + cos θJˆ
ˆI
In matrix form we can write this
ˆi cos θ sin θ ˆI
ˆ =
j − sin θ cos θ Jˆ
(7)
Similarly we can solve for ˆI and Jˆ in terms of ˆi and ˆj using the figure (or inverting Eq. 7) to get
ˆI cos θ − sin θ ˆi
ˆ =
J sin θ cos θ ˆj
(8)
Going back to our problem where the angle, θ, between the unit vectors is 20° we get
ˆi = cos 20°ˆI + sin 20°Jˆ
ˆj = − sin 20°ˆI + cos 20°Jˆ
which when substituted into Eq. 6 we get
r
v P = 0.120ω DE (− sin 20°ˆI + cos 20°Jˆ ) + v rel (cos 20°ˆI + sin 20°Jˆ )
= −0.041ω ˆI + 0.113Jˆ + 0.940 v ˆI + 0.342 v Jˆ
DE
rel
(9)
rel
Setting the right hands side of Eq. 9 and Eq. 1 equal to each other and equating components gives us Eqs. 4 and 5 again, that is, we get
the same answer we got earlier.
Now, let’s solve the acceleration problem using the coordinates defined in Option 1 and Option 2.
Option 1 (acceleration)
The absolute acceleration of point P is easily found by looking at link AP. Since P is attached to this link we simply recognize that P is
undergoing fixed axis rotation. Therefore, we get
4–61
r
r
r
r
a P = α AP × rP / A − ω 2AP rP / A
ˆ × (0.266 sin 25°ˆI + 0.266 cos 25°Jˆ ) − (5) 2 (0.266 sin 25°ˆI + 0.266 cos 25°Jˆ )
= −2 K
= −0.225Jˆ + 0.482ˆI − 2.810ˆI − 6.027Jˆ
= −2.328ˆI − 6.252Jˆ m/s 2
(10)
We can now find the acceleration of point P using the axis attached at point D. Since point P is not attached to body DE we need to use
the rotating axis equation given in Eq 4.16. The acceleration is
r
r
r
r
r
r
r
r
a P = a D + a rel + α DE × rP / D − ω 2DE rp / o + 2ω DE × v rel
(11)
We know the acceleration of point D is zero since it is a fixed pin and we also know the relative acceleration must be along the bar using
the same reasoning we used for the velocity. Therefore we know the direction of arel but not the magnitude. We also know the direction
of the angular acceleration of DE (in or out of the paper). Calculating each individual term (since there are so many) we get
r
aD
r
a rel
r
r
α DE × rP / D
r
− ω 2DE rp / o
r
r
2ω DE × v rel
=0
= a rel sin 70°ˆi + a rel cos 70°ˆj = 0.940a rel ˆi + 0.342a rel ˆj
= α DE kˆ × (0.120 sin 70°ˆi + 0.120 cos 70°ˆj) = 0.113α DE ˆj − 0.041α DE ˆi
= −(7.82) 2 (0.120 sin 70°ˆi + 0.120 cos 70°ˆj) = −6.896ˆi − 2.510ˆj
= 2(7.82kˆ ) × (−0.941 sin 70°ˆi − 0.941 cos 70°ˆj) = −13.830ˆj + 5.034ˆi
Substituting what we know into Eq. 11 we get
r
a P = (0.940a rel − 0.041α DE − 6.896 + 5.034)ˆi + (0.342a rel + 0.113α DE − 2.510 − 13.830)ˆj
= (0.940a − 0.041α − 1.862)ˆi + (0.342a + 0.113α − 16.34)ˆj
rel
DE
rel
(12)
DE
Setting Eq. 12 equal to Eq. 10 and equating components since the unit vectors are in the same direction we get:
ˆI (or ˆi ) :
−2.328 = 0.940a rel − 0.041α DE − 1.862
(13)
Jˆ (or ˆj) :
−6.252 = 0.342a rel + 0.113α DE − 16.34
(14)
Solving Eq. 4 and Eq. 5 we get arel = 3.00 m/s2 and αDE = 80.2 rad/s2. You’ll notice that in these problems there is quite a number of
cross products and algebra. Fortunately, these calculations can all be done in Maple. Before moving on to the coordinate system
defined in Option 2, let me show you the Maple code that will solve this problem. All we have to do is define our knowns, unknowns,
and to put in the two velocity equations (one for bar AP and the other for DE) and the two acceleration equations.
Load the linear algebra package, insert a : to inhibit output
> with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
Define the known quantities
> omegaAP:=vector([0,0,5]):
> alphaAP:=vector([0,0,-2]):
> rP_A:=evalf(vector([0.266*sin(25*Pi/180),0.266*cos(25*Pi/180),0])):
> rP_D:=evalf(vector([0.120*sin(70*Pi/180),0.120*cos(70*Pi/180),0])):
Define the unknown quantities
> VP:=vector([vpx,vpy,0]):
> Vrel:=evalf(vector([vrel*sin(70.*Pi/180),vrel*cos(70.*Pi/180),0])):
> omegaDE:=([0,0,wDE]):
> AP:=vector([apx,apy,0]):
> alphaDE:=([0,0,aDE]):
> Arel:=evalf(vector([arel*sin(70.*Pi/180),arel*cos(70.*Pi/180),0])):
4–62
Write the governing equation but move all the terms
to the same side of the equation.
> eq1:=evalm(crossprod(omegaAP,rP_A)-VP);
> eq2:=evalm(Vrel+crossprod(omegaDE,rP_D)-VP);
> eq3:=evalm(crossprod(alphaAP,rP_A)+crossprod(omegaAP,crossprod(omegaAP,rP_A))-AP);
>eq4:=evalm(crossprod(alphaDE,rP_D)+crossprod(omegaDE,crossprod(omegaDE,rP_D))+2*crossprod(
omegaDE,Vrel)+Arel-AP);
eq1 := [ −1.205389356− vpx, 0.5620822880− vpy, 0. ]
eq2 := [ 0.9396926210vrel − 0.04104241714wDE − vpx, 0.3420201428vrel + 0.1127631145wDE − vpy, 0. ]
eq3 := [ −2.328255697− apx, −6.251779695− apy, 0. ]
eq4 := [ −0.04104241714aDE − 0.1127631145wDE 2 − 0.6840402856wDE vrel + 0.9396926210arel − apx,
0.1127631145aDE − 0.04104241714wDE 2 + 1.879385242wDE vrel + 0.3420201428arel − apy, 0. ]
Form the scalar equations (this is the only unusual step in Maple). The output is suppressed.
> eqns1:={seq(eq1[k],k=1..2),seq(eq2[k],k=1..2),seq(eq3[k],k=1..2),seq(eq4[k],k=1..2)}:
Solve the equations
> sol:=evalf(solve(eqns1),5);
{ apy = -6.2518, vpx = -1.2054, apx = -2.3283, vpy = 0.56208, wDE = 7.8371, arel = 3.0443, aDE = 80.520,
vrel = -0.94045}
The answers are slightly different due to roundoff, but you’ll notice Maple makes this kind of problem very easy. Now let’s show how
to do the acceleration problem using the coordinate system defined in Option 2.
Option 2 (acceleration)
The acceleration of point P is still given by Eq. 10 and Eq. 11. The difference arises when we substitute into Eq. 11 as shown below.
r
r
r
r
r
r
r
r
a P = a D + a rel + α DE × rP / D − ω 2DE rp / o + 2ω DE × v rel
= 0 + a rel ˆi + α DE kˆ × 0.120ˆi − 7.8212 (0.120ˆi ) + 2(7.821kˆ ) × (−0.941ˆi )
= a ˆi + 0.120α ˆj − 7.340ˆi − 14.719ˆj
rel
(15)
DE
We again need to relate our two sets of unit vectors using the transformation:
ˆi = cos 20°ˆI + sin 20°Jˆ
ˆj = − sin 20°ˆI + cos 20°Jˆ
which when substituted Eq. 15 gives
r
a P = a rel (cos 20°ˆI + sin 20°Jˆ ) + 0.120α DE (− sin 20°ˆI + cos 20°Jˆ ) − 7.340(cos 20°ˆI + sin 20°Jˆ ) − 14.719(− sin 20°ˆI + cos 20°Jˆ )
= 0.940a ˆI + 0.342a Jˆ − 0.041α ˆI + 0.113α Jˆ − 6.897ˆI − 2.510Jˆ + 5.034ˆI − 13.831Jˆ
rel
rel
DE
DE
= (0.940a rel − 0.041α DE − 1.863)ˆI + (0.342a rel + 0.113α DE − 16.34)Jˆ
(16)
which is identical to Eq. 12. Setting the right hand side of Eq. 16 to that of Eq. 10 will result in the same set of scalar equations after
equating components and therefore will get the same answer we obtained using the coordinate system defined in Option 1.
4–63
Example 4/25
At Disney World there is a ride called “The Mad Hatter’s Tea Party”. The
ride consists of a large spinning disk. Attached to this disk are additional
spinning disks and attached to these disks are a number of tea cups which also
spin (naturally). A photograph of the ride is shown to the right and a
schematic diagram of a top view is shown below. I don’t remember how
many disks there were (or in what direction or how fast they rotated), so I am
just guessing. I’ve only included one cup to keep the figure from becoming
cluttered. The rider had the option of controlling the direction and speed of
rotation of the cup. Personally, I hated this ride because it made me very
dizzy, but unfortunately, my children loved it. Naturally, being a good father
I took them on it, but while riding I couldn’t help but think about the
dynamics (as I’m sure you would). Let’s assume all the angular velocities are
constant and the large disk rotates at 0.2 rad/s (CCW), the medium disk
rotates at 1.4 rad/s (CW) with respect to the large disk, and the cup rotates at
6 rad/s (CCW) with respect to the medium disk. Let’s define the distance
from A to C to be 12 feet, the distance from A to B
to be 5 feet and the distance from B to P to be 2
feet. A snapshot of a Working Model simulation of
these conditions is shown below so you can see the
P
actual path of point P.
B
ω3
a) At the instant shown, determine the velocity and
C
A
acceleration of point P.
b) The first time I went on this ride I let my kids
control the speed and direction of the cup (hence
ω2
my getting sick). The second time, however, I took
the controls and adjusted the speed and direction of
the cup so that it was in translation, that is, it was
not rotating at all. I found the ride rather enjoyable
but my kids said it was boring. What angular velocity did I choose for the cup?
ω1
Strategy: Since we are given angular velocities and are interested in finding the velocity and acceleration of a point, this is a pure
kinematics problem.
The first step is always to clearly define your reference frames. We
will use the ones defined below and shown in the figure.
OXY = fixed to ground
Ox1y1 = fixed to large disk
Ax2y2 = fixed to the medium disk with its origin at A
Bx3y3 = fixed to the cup with its origin at B
y3
ω3
Recall the equation relating the velocity expressed in any pair of
coordinate systems is
B
Y, y1
P
y2
A
x3
x2
O
X, x1
r r
r
r
r
v p = v o + v rel + ω × rp / o
ω2
All we have to do to solve this problem, is to use this equation several
times.
Motion of P (defined in Bx3y3) w.r.t. Ax2y2 (that is, assuming Ax2y2
were fixed, what would the velocity of P be?) We will call this
ω1
4–64
r
quantity v rel 2 , although in some books you will see
2
r
v P where the superscript on the upper right refers to the point, and the one on the
upper left, the coordinate system. For this part of the problem we have:
r
vo = 0
r
v rel = 0
r
ω = ω 3 kˆ = 6kˆ
r
r = 2ˆj
Substituting into our velocity equation we get the relative velocity of P with respect to A.
r
v rel2 = 0 + 0 + (6kˆ ) × 2ˆj
= −12ˆi
Motion of P (defined in Ax2y2) w.r.t. Ox1y1 (that is, assuming Ox1y1 were fixed, what would the velocity of P be?) The terms in our
velocity equation are
r
vo = 0
r
r
v rel = v rel 2 = −12ˆi
r
ω = ω 2 kˆ = −1.4kˆ
r
r = 7ˆj
Substituting into our velocity equation we get
r
v rel1 = 0 + −12ˆi + (−1.4kˆ ) × 7ˆj
= −12ˆi + 9.8ˆi = −2.2ˆi
Motion of P (defined in Ox1y1) w.r.t. OXY (that is, with respect to our fixed coordinate system).
r
vo = 0
r
r
v rel = v rel1 = -2.2ˆi
r
ω = ω1 kˆ = 0.2kˆ
r
r = −12ˆi + 7ˆj
Substituting into our velocity equation we get
r
v p = 0 + −2.2ˆi + (0.2kˆ ) × (−12ˆi + 7ˆj)
= −2.2ˆi − 2.4ˆj − 1.4ˆi
= −3.6ˆi − 2.4ˆj m/s
Now let’s do the acceleration problem in exactly the same manner. Recall the equation relating the acceleration expressed in any pair of
coordinate systems (for plane motion) is
r
r
r
r r
r
r r
a p = a o + a rel + α × rp / o − ω 2 rp / o + 2ω × v rel
All we have to do to solve this problem is to use this equation several times.
Motion of P (defined in Bx3y3) w.r.t. Ax2y2 (that is, assuming Ax2y2 were fixed, what would the acceleration of P be?) Using the same
r
type of notation we used for velocity, we will call this quantity a rel 2 . We know
r
ao = 0
r
a rel = 0
r
ω = ω 3 kˆ = 6kˆ
r
α=0
r
v rel = 0
r
r = 2ˆj
4–65
Substituting into our acceleration equation we get the relative acceleration of P with respect to A.
r
a rel2 = 0 + 0 + 0 − (6) 2 2ˆj + 0
= −72ˆj
Motion of P (defined in Ax2y2) w.r.t. Ox1y1 (that is, assuming Ox1y1 were fixed, what would the acceleration of P be?) The terms in our
acceleration equation are
r
ao = 0
r
r
a rel = a rel 2 = −72ˆj
r
ω = ω 2 kˆ = −1.4kˆ
r
α=0
r
r
v rel = v rel 2 = −12ˆi
r
r = 7ˆj
Substituting into our acceleration equation we get
r
r
a rel1 = 0 + −72 j + 0 − (−1.4) 2 7ˆj + 2(−1.4kˆ ) × (−12ˆi )
r
r
= −72 j − 13.72 j + 33.6ˆj
r
= −52.12 j
Motion of P (defined in Ox1y1) w.r.t. OXY (that is, with respect to our fixed coordinate system).
r
ao = 0
r
r
a rel = a rel1 = −52.12ˆj
r
ω = ω1 kˆ = 0.2kˆ
r
α=0
r
r
v rel = v rel1 = −2.2ˆi
r
r = −12ˆi + 7ˆj
Substituting into our acceleration equation we get
r
a p = 0 + (−52.12ˆj) + 0 − (0.2) 2 (−12ˆi + 7ˆj) + 2(0.2kˆ ) × (−2.2ˆi )
= −52.12ˆj + 0.48ˆi − 0.28ˆj − 0.88ˆj
= 0.48ˆi − 53.28ˆj m/s
b) Now, to the more important part of the question. More important, that is, if you are forced to take your children on a ride like this. If
you want the car to undergo translation, all you need to do is to choose the relative angular velocity of the cup to be such that the
absolute angular velocity is zero. We can find the absolute angular velocity of the cup since we know all the relative angular velocities
r
r
r
r
ω 3absolute = ω 3 / 2 + ω 2 / 1 + ω1
or using the notation defined in this problem,
r
r
r
r
ω 3absolute = ω 3 + ω 2 + ω1
= ω 3 kˆ − 1.4kˆ + 0.2kˆ
= (ω − 1.2)kˆ
3
To make the absolute angular velocity equal to zero, then the relative angular velocity of the
cup with respect to the medium disk must be equal to 1.2 rad/s. A Working Model simulation
showing the path of point P is shown in the accompanying figure. Clearly we still moved in a
curvilinear path, but our orientation never changes.
4–66
Example 4/26
Two slotted rods, AD and BE, are made to move such that
at the instant shown bar AD has a constant angular velocity
of 4 rad/s clockwise, bar BE has an angular velocity of 5 rad/s
counterclockwise and bar BE is slowing down at a rate of 2 rad/s2.
Determine the resulting force acting on the pin P at this instant assuming
the pin weighs 10 grams.
D
E
P
A
B
30°
300 mm
Strategy: Since we are asked for the force acting on the pin, we will need to use a conservation principle, in this case, the rate form of
conservation of linear momentum. Since we are given the angular motion of the two bars, we should be able to find the acceleration of
point P using kinematics. In this problem, we will need to use rotating axis since the pin is not attached to either bar. Let’s start with
LM rate.
KD
As a system we will start by looking at the pin. A FBD and KD are shown to the right.
m P a Py
LM x-direction (+ →)
r
dPx
=
dt
∑F
x
→
m P a Px = Px
Px
(1)
dt
=
∑
Fy
→
mPg
m P a Px
LM y-direction (+↑)
r
dPy
FBD
m P a Py = Py − m P g
Py
(2)
We have 2 equations and 4 unknowns ( a Px , a Py , Px , Py ) . To find the acceleration
of P we will use kinematics. Let’s start by defining some coordinate systems. We
will have one fixed coordinate system AXY, one rotating system attached to bar AD
called Ax1y1 and one attached to bar BE called Bx2y2 as shown.
Before we move on to our velocity and acceleration equations (we will need both
since our acceleration equation has relative velocity terms in it) let’s define our
position vectors.
r
r
r
rP / A = 0.3 tan (30°) j = 0.1732 j
r
r
rP / B = −0.3ˆi + 0.1732 j
D
E
P
y2
Y,y1
A
30°
X,x1
300 mm
Let’s now look at the velocity and acceleration of point P described in Ax1y1 with respect to the fixed frame AXY. The general velocity
and acceleration equations are
r r
r
r
r
v P = v o + v rel + ω × rP / o
r
r
r
r r
r
r r
a P = a o + a rel + α × rP / o − ω 2 rP / o + 2ω × v rel
r
We know the direction of the relative velocity, let’s call it v rel1 , because it must be along the slot. Therefore substituting into the
velocity equation we get
v p x ˆi + v p y ˆj = 0 + v rel1 ˆj + (−4kˆ ) × 0.1732ˆj
= v rel1 ˆj + 0.6928ˆi
B
x2
4–67
Equating components gives
ˆi :
v p x = 0.6928
(3)
ˆj :
v p y = v rel1
(4)
r
We can also substitute into the acceleration equation, again recognizing that the relative acceleration, let’s call it a rel1 , is along the slot.
a p x ˆi + a p y ˆj = 0 + a rel1 ˆj + 0 − (−4) 2 0.1732ˆj + 2(−4kˆ ) × v rel1 ˆj
= a rel1 ˆj − 2.7712ˆj + 8v rel1 ˆi
Equating components gives
ˆi :
ˆj :
a p x = 8v rel1
(5)
a p y = a rel1 − 2.7712
(6)
We now have 6 equations and 8 unknowns ( a Px , a Py , Px , Py , v p x , v p y v rel1 , a rel1 ) . We can get the additional equations we need by
looking at the velocity and acceleration of point P described in Bx2y2 with respect to the fixed frame AXY. We know the direction of
r
the relative velocity, let’s call it v rel 2 , because it must be along the slot. In this case it will have both an X and a Y component.
Substituting into the velocity equation we get
v p x ˆi + v p y ˆj = (− v rel 2 cos(30°)ˆi + v rel2 sin(30°))ˆj + (5kˆ ) × (−0.3ˆi + 0.1732ˆj)
= −0.866 v rel 2 ˆi + 0.500 v rel 2 ˆj − 1.5ˆj − 0.866ˆi
Equating components gives
ˆi :
ˆj :
v p x = − 0.866v rel2 − 0.866
(7)
v p y = 0.500v rel2 − 1.5
(8)
r
We can also substitute into the acceleration equation, again recognizing that the relative acceleration, let’s call it a rel 2 , is along the slot.
a p x ˆi + a p y ˆj = (−0.866a rel2 ˆi + 0.500a rel 2 ˆj) + (−2kˆ ) × (−0.3ˆi + 0.1732ˆj) − (5) 2 (−0.3ˆi + 0.1732ˆj) + 2(5kˆ ) × (−0.866 v rel2 ˆi + 0.500 v rel 2 ˆj)
= −0.866a rel 2 ˆi + 0.500a rel 2 ˆj + 0.6ˆj + 0.3464ˆi + 7.5ˆi − 4.335ˆj − 8.66 v rel 2 ˆj − 5.00 v rel 2 ˆi
= (−0.866a rel2 + 7.8464 − 5.00 v rel2 )ˆi + (0.500a rel 2 − 3.735 − 8.66 v rel 2 )ˆj
Equating components gives
ˆi :
ˆj :
a p x = − 0.866a rel2 + 7.8464 − 5.00 v rel2
(9)
a p y = 0.500a rel2 − 3.735 − 8.66 v rel2
(10)
We now have 10 equations and 10 unknowns ( a Px , a Py , Px , Py , v p x , v p y , v rel1 , a rel1 , v rel2 , a rel2 ) which we can solve in Maple.
Instead of obtaining the scalar equations for the kinematics by hand (which is a perfectly fine way to do it and you should be able to do
cross products by hand) we could have just put the vector equations into Maple and let it do the cross products for us. The Maple code
to do this is shown.
4–68
The final answer for the force on P is Px = -0.192 N and Py = 0.425 N
How could I have made this problem a bit more challenging? It is always possible to make the geometry more complicated, but another
easy way would have been to make one of the bars curved as
D
shown below. I’d have to give you some additional dimensions,
of course, but what will have to change in your solution assuming
all the angular velocities and accelerations remain the same?
E
It turns out that the velocity problem will remain essentially the
same. Of course the position vector will change to
R=150 mm
r
r
rP / A = 0.100ˆi + 0.1732 j , but other than that the equations will
remain essentially unchanged. The main difference will be in the
relative acceleration for bar AD. Since P is now traveling along a
curved path the relative acceleration will have two components
rather than one, so for bar AD it will be
r
a rel1 = −
v 2rel1
R
P
30°
A
ˆi + a ˆj
rel1
Other than that, the procedure to solve the problem is identical to
what we just did.
100 mm
300 mm
B
4-69
Problems
Problem 4.4
Disk A has a mass of 6 kg and an initial angular velocity of 360
rpm clockwise; disk B has a mass of 3 kg and is initially at rest.
The disks are brought together by applying a horizontal force of
magnitude 20 N to the axle of disk A. The coefficient of kinetic
friction between the disks is µk = 0.15. Bearing friction can be
neglected. Determine:
a) the angular acceleration of each disk,
b) the final angular velocity of each disk.
Problem 4.1
When the power to an electric motor is turned
on, the motor reaches its rated speed of 3300
rpm in 6 s, and when the power is turned off,
the motor coasts to rest in
80 s. Assume uniformly accelerated motion.
Determine the number of revolutions that the
motor executes in a) reaching its rated speed,
b) coasting to rest.
A
Problem 4.2
Two blocks and a pulley are connected by inextensible cords as
shown. The pulley has an initial angular velocity of ω = 0.8
rad/s counterclockwise and a constant angular acceleration of α
= 1.8 rad/s2 clockwise. After 5 s of motion, determine the
velocity and position of block A and block B.
B
80 mm
60 mm
C
200 mm
90 mm
A
B
Problem 4.3
Three bars, each weighing 8 lbs, are welded together and are
pin-connected to links BE and CF. The weight of the links can
be neglected (this means that each link can be considered as a 2force member, that is, the force acts along the link). If the system
is released from rest, determine the force in each link
immediately after release.
15 in.
A
A
15 in.
E
50°
C
F
weld
80 mm
C
A
B
120 mm
D
B
Problem 4.5
A 1.5 kg slender rod is welded to a 5 kg uniform disk as shown.
The assembly swings freely about C in a vertical plane. In the
position shown, the assembly has an angular velocity of ω = 10
rad/s clockwise. Determine a) the angular acceleration of the
assembly, and b) the components of the reaction at C.
50°
4-70
Problem 4.6
A slender 4 kg rod can rotate in a vertical plane about a pivot at
B. A spring having a constant of k = 400 N/m and unstretched
length of l = 150 mm is attached to the rod as shown. The rod is
released from rest in the position shown. Determine the angular
velocity of the rod after it rotates through 90°.
A
Problem 4.8
A 3-in.-radius drum is rigidly attached to a 5-in.-radius drum as
shown. One of the drums rolls without sliding on the surface
shown, and a cord is wound around the other drum. End E of the
cord is pulled to the left with a velocity of v = 6 in/s. Determine:
a) angular velocity of the drums
b) velocity of the center of the drums
c) length of cord wound or unwound per second.
5 in.
600 mm
A
D
B
C
B
E
120 mm
3 in.
D
k
350 mm
Problem 4.7
A 45-g bullet is fired with a horizontal velocity of 400 m/s into a
9-kg panel of side b = 0.2 m. Knowing that h = 190 mm and that
the panel is initially at rest, determine
a)the velocity of the center of the panel immediately after the
bullet becomes imbedded,
b)the impulsive reaction at A, assuming that the bullet becomes
imbedded in 2 ms.
c)the reaction at A after the plate has swung through an angle of
90 degrees
Problem 4.9
At the instant shown, the angular velocity of rod AB is ω = 15
rad/s clockwise. Determine:
a) Angular velocity of rod BD
b)Velocity of the midpoint of rod BD
A
0.2 m
B
A
h
b
0.25 m
C
D
v0
b
0.2
0.6 m
4-71
Problem 4.10
A slender rod of length l is pivoted about a point C located at a
distance b form its center G. It is released from rest in a
horizontal position and swings freely. Determine:
a) The distance b for which the angular velocity of the rod as it
passes through a vertical position is maximum
b)Corresponding values of its angular velocity and of the
reaction at C.
Problem 4.12
The uniform rods AB and BC weigh 2.4 pounds and 4 pounds,
respectively. Assume the small wheel at C is of negligible
weight. Determine the velocity of the pin B after rod AB has
rotated through 90º.
B
30 in
b
18 in
A
B
C
G
C
A
P = 2 lbf
l
Problem 4.11
Rod BC (m = 5 kg) is attached by pins to two uniform disks as
shown. The mass of the 150-mm-radius disk is 6 kg, and that of
the 75-mm-disk is 1.5 kg. The system is released from rest in
the position shown, the disks roll without slipping on the ground
and a constant moment, M = 2 N-m is applied to the larger disk
as shown. Determine the velocity of the center of gravity of the
rod after disk A has rotated through 90°.
Problem 4.13
The 80-mm-radius gear shown below has a mass of 5 kg and a
centroidal radius of gyration of 60 mm (the gear teeth are left off
the drawing because they are a pain to draw). The 4-kg rod AB
is attached to the center of the gear and to a pin at B that slides
freely in a vertical slot. Knowing that the system is released
from rest when θ = 60º, determine the velocity of the center of
the gear, A, when θ = 0.
80 mm
no slipping
A
M
75 mm
θ
320 mm
150 mm
A
B
B
C
75 mm
4-72
Problem 4.14
At what height h above its center G should a billiard ball of
radius r be struck horizontally by a cue if the ball is to start
rolling without sliding?
h
G
Problem 4.16 (Taken from Engineering Mechanics: Dynamics
by Meriam and Kraige)
Each of the two 300-mm rods A has a mass of 1.5 kg and is
hinged at its end to the rotating base B. The 4-kg base has a
radius of gyration of 40 mm and is initially rotating freely about
its vertical axis with a speed of 300 rev/min and with the rods
latched in the vertical positions. If the latches are released and
the rods assume the horizontal positions, calculate the new
rotational, N, speed of the assembly in rev/min.
Problem 4.15
The uniform rectangular block shown below is moving along a
frictionless surface with a velocity v1 when it strikes a small
obstruction at B. Assuming that the impact between corner A
and obstruction B is perfectly plastic, determine the magnitude
of the velocity v1 for which the maximum angle θ through which
the block will rotate is 30º.
10 in.
5 in.
v1
A
θ
B
Problem 4.17
The 6-lb steel sphere A and the 10-lb wooden cart B are at rest in
the position shown below when the sphere is given a slight
nudge, causing it to roll without sliding along the top surface of
the cart. Assume the friction between the cart and the ground is
negligible. Determine the velocity of the cart as the sphere
passes through the lowest point of the surface at C. Note:
assume the radius of the sphere is r. Your final answer should
not depend on r.
A
6 in.
C
B
4-73
Problem 4.18
A 900-mm rod rests on a horizontal table. A force P applied as
shown produce the following accelerations: aA = 3.6 m/s2 to the
right, α = 6 rad/s2. Determine the point on the rod that a) has no
acceleration, b) has an acceleration of 2.4 m/s2 to the right.
Problem 4.21
Knowing that crank AB rotates about point A with a constant
angular velocity of 900 rpm clockwise, determine the
acceleration of the piston P when θ = 120°.
P
D
B
0.45 m
G
150 mm
0.45 m
P
A
A θ
Problem 4.19
An automobile travels to the left at a constant speed of 48 mi/h.
Knowing that the diameter of the wheel is 22 in., determine the
acceleration a) of point B, b) of point C, c) of point D.
B
D
30°
B
50 mm
Problem 4.22
Knowing that at the instant shown rod AB has a constant angular
velocity of 6 rad/s clockwise, determine a) the angular
acceleration of member BDE, b) the acceleration of point E.
48 mi/h
E
22 in
90 mm
D
90 mm
C
Problem 4.20
The endpoints of the bar slide on the plane surfaces. Show that
the acceleration of the midpoint G is related to the bar's angular
velocity and angular acceleration by
[(
B
90 mm
) (
)]
L
v
aG =
α cos θ − ω2 sin θ ˆi − α sin θ + ω2 cos θ ˆj
2
θ
C
A
225 mm
225 mm
40 mm
Problem 4.23
A uniform slender rod AB rests on a frictionless horzontal
surface,and a force P of magnitude 0.25 lb is applied at A in a
direction perpendicular to the rod. Knowing that the rod weighs
1.75 lb, determine the acceleration of a) point A, b) point B.
L
y
α
G
P
A
ω
x
36 in.
B
z
4-74
Problem 4.27
A uniform slender bar AB of mass m is suspended as shown
from a uniform disk of the same mass m. Assuming the disk
rolls without slipping on the ground, determine the accelerations
of points A and B immediately after a horizontal force P has
been applied at B.
Problem 4.24
The 3-oz yo-yo shown has a centroidal
radius of gyration of 1.25 in. The radius of
the inner drum on which a string is wound
is 0.25 in. Knowing that at the instant
shown the acceleration of the string is 3
ft/s2 upward, determine a) the tension in the
string, b) the corresponding angular
acceleration of the yo-yo.
A
Problem 4.25
A bowler projects an 8-in diameter ball weighing 12 lb along an
alley with a forward velocity of 15 ft/s and a backspin of 9 rad/s.
Knowing that the coefficient of kinetic friction between the ball
and the alley is 0.10, determine
a) the initial acceleration of the center of gravity of the ball
b) the initial angular acceleration of the ball
c) the time t1 at which the ball will start rolling without slipping
d) the speed the ball at time t1
e) the distance the ball will have traveled at time t1
f) the friction force immediately after the ball starts rolling
without slipping.
ω0
v0
r
L
B
P
Problem 4.28
A meterstick having a mass of 0.1 kg is released from rest in the
position shown. Model the meterstick as a slender bar and
assume it is released from rest at θ0 = 30° and all surfaces are
frictionless.
Determine
a) the normal force between the stick and the vertical wall at
any angle θ.
Problem 4.26
A drum of 60-mm radius is attached to a disk of 120-mm radius.
The disk and drum have a total mass of 6 kg and a combined
radius of gyration of 90 mm. A cord is attached as shown and
pulled with a force P of magnitude 20N. Knowing that the disk
rolls without slipping, determine
a) the angular acceleration of the disk and the acceleration of G
b) the minimum value of the coefficient of friction compatible
with this motion.
P
70°
G
To check your answer:
when θ = 30° you should get α = 7.36 rad/s2, and NB = 0.32 N
when θ = 40° you should get α = 9.46 rad/s2, and NB = 0.27 N
b) Determine the angle the bar will leave the wall assuming the
bar is released from rest at angle θ0 = 30° (i.e. at what angle will
the normal force between the vertical wall and the yardstick to
zero). It is helpful to determine the normal force and plot it as a
function of θ to get a feel for when it will be zero. Include this
plot in your solution.
c)Use Working Model determine the angle the bar will leave the
wall. Be sure to use all the same parameters as used in part b).
In your WM simulation define a measure giving the normal
force between the wall and the meterstick by selecting both
objects and then going to the “Measure” menu and selecting
“contact force”. Include a snapshot of the simulation at the
moment the meterstick leaves the wall.
d) Compare your results from part b) and c)
Hints:
1) You need the angular velocity for any angle θ. The easiest
way is to determine this is to use conservation of energy between
some starting angle θ0 and some final angle θ. You should be
4-75
able to obtain ω =
3g
(cos θ0 − cos θ) . To save time in
L
solving this problem you may assume this relationship is given
(just be sure that you could derive it if asked!)
2) You’ll need the acceleration of the center of gravity as a
function of θ which you found in problem 20.3 to be
[(
)]
) (
L
v
aG =
α cos θ − ω2 sin θ ˆi − α sin θ + ω2 cos θ ˆj You do
2
not need to rederive this if you have already done this problem.
3) In you Working Model solution make sure friction is zero.
3) Use Maple to solve the set of equations that you will get.
Problem 4.30
In the engine system shown L = 250 mm and b = 100 mm. The
connecting rod BD is assumed to by a 1.2 kg uniform slender
rod and is attached to the 1.8 kg piston P. During a test of the
system, crank AB is make to rotate with a constant angular
velocity of 600 rpm clockwise with no force applied to the face
of the piston. Determine the forces at B and D on the connecting
rod as functions of θ and make plots of Bx, By. Dx and Dy. The
figure shown is a top view so you will not have the weights on
the FBDs.
L
B
b
P
θ
D
A
y
θ
L
x
α
G
ω
Problem 4.29
A driver starts his car with the door on the passenger’s side wide
open (θ = 0). The 80 lb door has a centroidal radius of gyration
of 12.5 in and its mass center is located at a distance r = 22 in.
from its vertical axis of rotation, A. Knowing that the driver
maintains a constant acceleration of 6 ft/s2. Determine the
angular velocity of the door as it slams shut (θ = 90°).
a
A
B
θ
Hints:
• You will need to write your position vectors for some
general angle θ.
• In order for crank AB to rotate at a constant angular
velocity there must be a moment applied to it, so do not
pick AB as one of your systems since you are not asked to
determine this moment.
• Using kinematics you should be able to determine the
acceleration of the center of gravity of BD so the only
systems you will need to use are bar BD and the piston
(both by themselves).
An answer to check you Maple worksheet is shown below:
When θ = 180° the forces are: B = 805 N (left), D = 426 N
(right). A plot of Bx as a function of θ is shown to the right.
4-76
Problem 4.31 (from Vector Mechanics for Engineers:
Dynamics by Beer and Johnston)
Problem 4.33 (from Vector Mechanics for Engineers:
Dynamics by Beer and Johnston)
Two rotating rods are connected by slider block P. The rod
attached at A rotates with a constant angular velocity of 10 rad/s
clockwise. Determine:
a) the angular velocity of the rod attached at B,
b) the relative velocity of slider block P with respect to the rod
on which it slides.
At the instant shown bar BC has a constant angular velocity of 2
rad/s counterclockwise. Determine the angular acceleration of
the plate.
40 mm
B
A
D
30 mm
D
P
60°
A
B
20°
C
40 mm
300 mm
Problem 4.32 (from Vector Mechanics for Engineers:
Dynamics by Beer and Johnston)
The hydraulic cylinder CD is welded to an arm which rotates
clockwise about A at a constant rate ω = 2.4 rad/s. Knowing that
in the position shown BE is being moved to the right at a
constant rate of 15 in/s with respect to the cylinder, determine, a)
the velocity of point B, b) the acceleration of point B.
60 mm
Problem 4.34
Two rotating rods are connected by slider block P. Neglect
friction between the slider block and bar AD. The rod attached
at A rotates with a constant angular velocity of 10 rad/s
clockwise. Determine:
a) the angular acceleration of the rod attached at B,
b) the relative acceleration of slider block P with respect to the
rod on which it slides.
c) If bar AB has a mass of 5 kg the mass of the slider is
negligible, determine the reactions at point B.
Hint: Use the velocities you found in problem 28.1.
A
D
ω
7.5 in
B
C
D
E
P
10 in
10 in
60°
A
20°
300 mm
B
Problem 4.35
The uniform 60 lb log is supported by two cables and used
as a battering ram. If the log is released from rest in the
position shown, determine
a) the tension in each cable immediately after release
b) the corresponding angular acceleration of the cables.
c) the tension in each cable when the cables are vertical.
Problem 4.37
A gear reduction system consists of three gears A, B, and
C. Gear A starts from rest at time t = 0 and rotates
clockwise with constant angular acceleration. Knowing
that the angular velocity of gear A is 600 rpm at time t = 2
s, determine (a) the angular accelerations of gears B and
C, (b) the accelerations of the points on gears B and C
which are in contact when t = 0.5 s.
50 mm
2’
60°
2’
2’
60° 1’
A
B
60 lb
C
Problem 4.36
Two blocks A and C are welded together and they rest on
top of wedge B. Incline B has a weight, WB, block A has
a weight, WA and block C has a weight, WC. The
parameters, w, h1, h2, and θ are all known.
a)
Assuming the friction between A and B is large
enough to prevent sliding, determine the equations
necessary to find the force, F, so that block A does
not tip in a counterclockwise direction.
b) Using w = 0.8”, h1 = 0.8”, h2 = 0.4”, WA = 1 lbf, WB
= 2 lbf, WC = 0.4 lbf, and θ=20°, determine a
numerical value for F.
c) Assuming F = 0 and the friction between block A and
B is magically reduced to zero and block A does not
tip, determine the velocity of block A and block B
after A has moved a distance d=3” down the incline.
w
C
A
F
C
B
A
h2
B
µ=0
h1
θ
50 mm
100 mm
150 mm
Problem 4.38
A bar is pinned at point O and a moveable mass is
attached to it as shown. The system is released from rest
in the horizontal position and a sensor is attached to the
top of the bar to measure its angular position. The system
has the following nominal parameter values:
mp = pendulum mass = 68.5 g
mw = moveable weight = 88 g
Lp = pendulum length = 43.2 cm
ds = Sensor diameter = 2.5 cm
dw = moveable weight diameter = 5 cm
Assuming the pendulum rod is mounted flush with the top of the
sensor, and moveable weight is not moved lower than flush with
bottom edge of pendulum rod, we would observe that.
Lcg_min = minimum location for moveable mass = (ds+dw)/2
Lcg_max = maximum location for moveable mass = Lp - (ds+dw)/2
L_cg_pendulum =location of the pendulum center of gravity=(Lp-ds)/2
Determine:
a) Plot the angular velocity of the pendulum when it is vertical
as a function of the location of the moveable mass.
b) Determine the location, Lcg, that will maximize the
angular velocity when the bar is vertical.
O
Problem 4.39
A 45-g bullet is fired with a velocity of 400 m/s into a 9kg panel of side b = 0.2 m as shown. Knowing that the
bullet strikes the plate at a height h = 190 mm and that the
panel is initially at rest, determine
a) the velocity of the center of the panel immediately
after the bullet becomes imbedded,
b) the impulsive reaction at A, assuming that the bullet
becomes imbedded in 2 ms.
c) the reaction at A after the plate has swung through an
angle of 90 degrees
Problem 4.41
The gear has a mass of 2 kg and a radius of gyration of 0.19
m. The connecting link (slender rod) and the slider block at
B have a mass of 4 kg and 1 kg, respectively. If the gear is
released from rest in the position where θ = 30º, determine
the angular velocity of the gear when θ = 0º. Only a portion
of the two tracks are shown.
Position 1
0.2 m
A
45°
Note: For part c) neglect the mass of the bullet since you
do not know exactly where it will become lodged in
the plate.
Gear
θ =30°
B
A
h
0.6 m
b
30°
v0
Problem 4.42
A homogeneous cylindrical disk of mass m rolls without
slipping on the horizontal surface with angular velocity ω.
If it does not slip or leave the slanted surface when it comes
into contact with it, determine the maximum elevation, hfinal
that the disk will achieve.
b
Problem 4.40
A slender 4 kg rod can rotate in a vertical plane about a pivot at
B. A spring having a constant of k = 400 N/m and unstretched
length of l = 150 mm is attached to the rod as shown. The rod is
released from rest in the position shown. Determine the angular
velocity of the rod after it rotates through 90°.
Determine
a) the angular velocity of the rod after it has rotated
through 90°
b) the reactions at point B after the rod has rotated
through 90°
A
600 mm
D
B
120 mm
C
k
350 mm
ω
R
hfinal
θ
A1
Appendix A - Mass Moments of Inertia
In this appendix I will tell you all you need to know about mass moments of inertia
(at least for this class).
A.1 What is the mass moment of inertia?
The mass moment of inertia is a measure of an objects resistance to rotation,
similar to mass being a measure of an objects resistance to translation. It depends
on the distribution of mass of an object and the axis about which the mass moment
of inertia is to be calculated. The mass moment of inertia is defined to be:
∫
I = r 2 dm
The mass moments of inertia for some common shapes are shown on the following
page.
Parallel Axis Theorem
Given the mass moment of inertia about an axis passing through the center of
gravity, the mass moment of inertia about an axis passing through any other point
may be determined using the parallel axis theorem as shown below:
I O = I G + mr 2
where
r = the distance between G and O
IO = mass moment of inertia about an axis passing though O
IG = mass moment of inertial about the center of gravity.
Radius of Gyration
The radius of the gyration is the quantity that when squared and multiplied by the
mass you get the mass moment of inertia. That is
I O = mk O2
where
kO = the radius of gyration about point O
m = mass of the object
IO = mass moment of inertia of the object about an axis passing through O.
It is basically just an alternative way of giving you the mass moment of inertia.
A2
Mass moment of Inertia of some Common Shapes
Solid Sphere
Ix = Iy = Iz =
z
2 2
mr
5
y
r
G
x
Slender Rod
Iy = Iz =
z
y
1
mL2
12
G
L
Solid Circular Cylinder
1
I x = mr 2
2
1
Iy = Iz =
m L2 + 3r 2
12
(
y
G
)
x
z
(
y
r
G
x
Thin Rectangular Plate
1
m b2 + h2
12
1
Iy =
mh 2
12
1
Iz =
mb 2
12
r
L
Thin Disk
1
I x = mr 2
2
1
I y = I z = mr 2
4
Ix =
x
z
z
)
y
G
h
x
b
Brick
(
(
(
1
m b2 + h2
12
1
Iy =
m h2 + d2
12
1
Iz = m b2 + d2
12
Ix =
)
)
)
b
z
y
h
G
d
x